Разработка системы итогового повторения курса алгебры 7 – 9. Учитель МБОУ СОШ с. Царевщина Балтайского р-на Саратовской области Ерофеева Т.В.
« Разработка системы итогового повторения курса алгебры 7-9 классов»
Проведение итогового повторения по математике ориентировано на подготовку к сдаче итоговой аттестации в виде тестирования, где учащиеся должны продемонстрировать результаты овладения школьного курса математики.
Занятия предназначены для оказания индивидуальной помощи при изучении математики в школе, для восстановления и закрепления знаний, полученных во время изучения той или иной темы, для развития навыков решения широкого круга задач, встречающихся на экзаменах.
Подготовка к итоговой аттестации организована так, чтобы как можно полнее охватить все разделы математики, используемые в тестах на ГИА. На занятиях в доступной форме рассматриваются решения задач и примеров, тематика которых соответствует прототипам заданий, предложенных в демоверсиях. Решение заданий рассматривается подробно, с пошаговым объяснением, методическими рекомендациями и анализом предполагаемых ошибок. Контроль осуществляется с помощью тематических тестов.
Основная цель итогового повторения – повышение качества знаний, умений и навыков, необходимых выпускнику на итоговом тестировании.
Задачи:
- создание прочной и надежной базы, которая поможет учащемуся продемонстрировать определенную системность знаний и широту представлений, умение переходить с одного математического языка на другой, узнавать стандартные задачи в разнообразных формулировках, применять свои знания в практических ситуациях;
- способствование развитию мышления коммуникативной культуры учащихся;
- формирование ответственности за результат итоговой аттестации.
Примерное планирование учебного времени
по итоговому повторению курса алгебры 7-9 классов.
№ п/п
Темы занятий
Кол-во часов
1.
Числа и вычисления
2
2.
Проверочная работа №1
1
3.
Алгебраические выражения
2
4.
Проверочная работа №2
1
5.
Уравнения. Системы уравнений.
3
6.
Проверочная работа №3
1
7.
Неравенства. Системы неравенств
2
8.
Проверочная работа №4
1
9.
Последовательности и прогрессии
2
10.
Проверочная работа №5
1
11.
Функции
2
12.
Проверочная работа №6
1
13.
Решение вариантов пробных тестов по ГИА
3
14.
Итоговое проверочное тестирование
2
15.
Анализ итоговой работы
1
Всего часов
25
Примерные тематические тестовые работы.
Проверочная работа № 1 по теме «Числа и вычисления».
Соотнесите обыкновенные дроби с равными им десятичными.
А.  Б.
Б.  В.
В.  Г.
Г.  1) 0,5 2) 0,02 3) 0,12 4) 0,625
1) 0,5 2) 0,02 3) 0,12 4) 0,625
Какому из выражений равно произведение
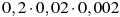 ?
?
1.
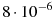
2.
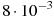
3.
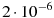
4.
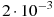
3. Запишите в ответе номера тех выражений, значение которых равно -5.
1) 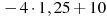 2)
2) 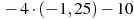 3)
3) 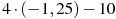 4)
4) 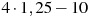
4. Расположите в порядке возрастания числа: 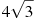 ,
, 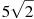 , 6.
, 6.
1) 6; 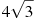 ;
;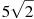 ; 2)
; 2) 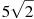 ; 6;
; 6; 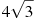 ; 3)
; 3) 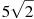 ;
; 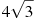 ; 6; 4)
; 6; 4) 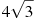 ;
; 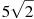 ; 6.
; 6.
5. Какое из чисел отмечено на координатной прямой точкой A?

1.

2.

3.

4.
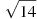
6. О числах a и c известно, что 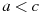 . Какое из следующих неравенств неверно?
. Какое из следующих неравенств неверно?
1.
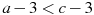
2.
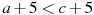
3.
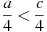
4.
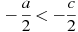
7. Найдите значение выражения 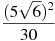 .
.
1.
1080
2.
1
3.
216
4.
5
8. Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
1.
960 р.
2.
820 р.
3.
160 р.
4.
1600 р.
9. Расстояние от Земли до Солнца равно 1,5·1011м. выразите это расстояние в миллиметрах.
1) 1,5·1015; 2) 1,5·1014; 3) 1,5·1013; 4) 1,5·1012.
Проверочная работа № 2 по теме «Алгебраические выражения».
Найдите значение выражения
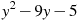 при
при 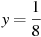 .
.Найдите значение выражения
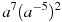 при
при  .
.1.
-125
2.
125
3.
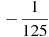
4.

Найдите значение выражения
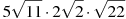 .
.
Сравните числа x и y, если
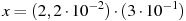 ,
, 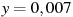 .
.Найдите значение выражения
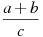 при
при 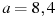 ;
; 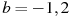 ;
; 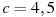 .
.
Чтобы перевести значение температуры по шкале Цельсия (
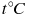 ) в шкалу Фаренгейта (
) в шкалу Фаренгейта (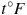 ) пользуются формулой
) пользуются формулой 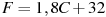 , где С — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует
, где С — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует  по шкале Цельсия?
по шкале Цельсия?Из физической формулы
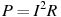 выразите переменную I (все величины положительны).
выразите переменную I (все величины положительны).Какой из следующих квадратных трехчленов нельзя разложить на множители?
1.
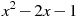
2.
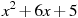
3.
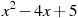
4.
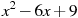
Укажите выражение, тождественно равное дроби
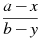 .
.1.
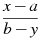
2.
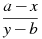
3.
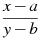
4.
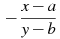
Преобразуйте в многочлен выражение
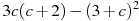 .
.Упростите выражение
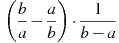 .
.При каком значении x выражение
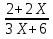 не имеет смысла?
не имеет смысла?
2; 2) -2; 3) -1; 4) 0.
Сократите дробь
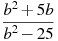 .
.
Разложите на множители x2 - y2 - 2x - 2y.
Проверочная работа № 3 по теме «Уравнения. Системы уравнений».
Какое из чисел является корнем уравнения х3 – х2 + 2х + 16 = 0?
3; 2) -2; 3) -1; 4) 0.
Решите уравнение
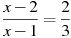 .
.Какое из уравнений имеет бесконечное число корней?
0·х=1; 2) 0·х=0; 3) 0 + х=0; 4) 0 - х=0.
Решите уравнение
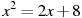 .
. Решите уравнение
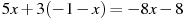 .
.Моторная лодка прошла по течению реки 15 км и вернулась обратно, затратив на обратный путь на 40 минут больше. Скорость течения реки 3 км/ч.
Пусть х км/ч – собственная скорость лодки. Какое из уравнений соответствует условию задачи?
1)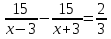 ; 2)
; 2)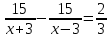 ; 3)
; 3)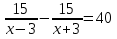 ; 4)
; 4)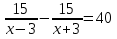 .
.
7. Решите систему уравнений 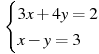
8. Вычислите координаты точек пересечения параболы 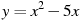 и прямой
и прямой 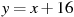 .
.
9. Окружность, изображенная на рисунке, задана уравнением 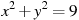 . Используя этот рисунок, определите, какая из систем уравнений не имеет решений.
. Используя этот рисунок, определите, какая из систем уравнений не имеет решений.
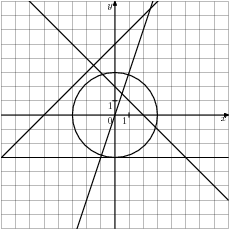
1.
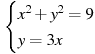
2.
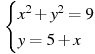
3.
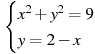
4.
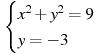
10. Решите систему уравнений 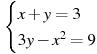 .
.
Проверочная работа № 4 по теме «Неравенства. Системы неравенств».
О числах a и c известно, что
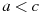 . Какое из следующих неравенств неверно?
. Какое из следующих неравенств неверно? 1.
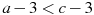
2.
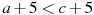
3.
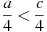
4.
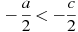
О числах a, b, c и d известно, что
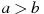 ,
, 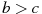 ,
, 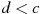 . Сравнитe числа d и a.
. Сравнитe числа d и a. 1.
d=a
2.
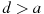
3.
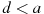
4.
Сравнить невозможно.
Решите неравенство 6х – 4(х – 2)≤ 4х + 16.
(-∞; -4]; 2) [ 4; +∞); 3) (-∞; 4]; 4) [- 4; +∞).
Решите неравенство
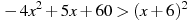 .
.
Решите систему неравенств

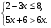
Решений нет; 2)
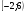 ; 3)
; 3) 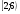 ; 4)
; 4) 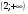 .
.
Укажите неравенство, решением которого является любое число.
Х2 + 25 < 0; 2) х2 – 25 < 0; 3) х2 + 25 > 0; 4) х2 – 25 > 0.
Решите неравенство (3 – 2х)(х – 5)< 0.
Решите неравенство
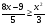 .
.
Найдите область определения выражения.
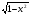
Укажите наименьшее целое решение системы неравенств.
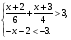
Проверочная работа № 5 по теме «Последовательности и прогрессии».
Последовательность задана формулой
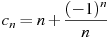 . Какое из следующих чисел не является членом этой последовательности?
. Какое из следующих чисел не является членом этой последовательности?1.

2.

3.
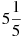
4.

Последовательности заданы несколькими первыми членами. Одна из них — арифметическая прогрессия. Укажите ее.
1.
"1;2;3;5"
2.
"2;4;6;8"
3.
"1;
 ;
; ;
; "
" 4.
"1;3;9;27"
В первом ряду кинозала 28 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером n?
1.
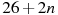
2.
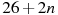
3.
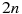
4.
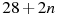
Дана арифметическая прогрессия: 42; 39; 36; … . Найдите первый отрицательный член этой прогрессии.
1.
-5
2.
-3
3.
-4
4.
-2
Последовательность задана условиями
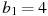 ,
, 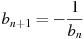 . Найдите
. Найдите 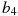 .
.
Выписано несколько последовательных членов арифметической прогрессии: …; 11; х; –13; –25; … . Найдите член прогрессии, обозначенный буквой х.
Между числами 2 и 32 вставьте такие три числа, которые вместе с данными числами образуют геометрическую прогрессию.
Найдите сумму семи первых членов геометрической прогрессии 4; 8;… .
Сколько положительных членов в последовательности Сn, заданной формулой Сn=23 – 3n?
В геометрической прогрессии сумма первого и второго членов равна -12, а сумма второго и третьего членов равна 16. Найдите первых три члена этой прогрессии.
Проверочная работа № 6 по теме «Функции».
1. На рисунке изображен график квадратичной функции у=f(x). Используя рисунок, выясните, какое утверждение неверно.
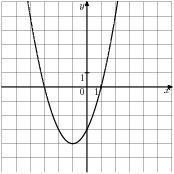
1.Если х= -3, то
2. f(-2)< f(1);
3.Нули функции
4. f(x)>0 при х>0
Ответ:__________
f(x)
=0;
-3 и 1;
2.Функция задана формулой у=4х3+2х2- 5х -15. Найдите значение функции при х=-2.
3.Найдите область определения функции у =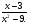
1)х‡3; 2) х‡-3; 3) х‡3 и х‡-3; 4) х - любое число.
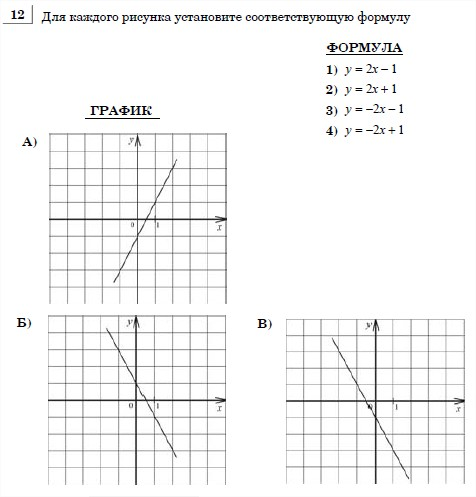
4. Установите соответствие между графиками функций и формулами, которые их задают.
А)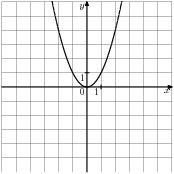 Б)
Б)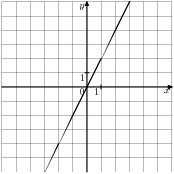 В)
В) 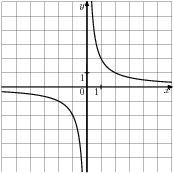
А
Б
В
1) 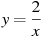 ; 2)
; 2) 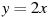 ; 3)
; 3) 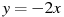 ; 4)
; 4)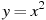 . Ответ:
. Ответ:
5. Какая из функций является возрастающей?
1) у = 6х2; 2) у = 2х-8; 3) у =-3х + 5; 4) у = -2х2.
6.Вычислите координаты вершины параболы у=3х3 – 6х +5.
7. В какой координатной четверти находится точка пересечения прямых 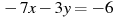 и
и 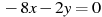 ?
?
1.
В I четверти
2.
В II четверти
3.
В III четверти
4.
В IV четверти
8. Длина лыжной дистанции составляет 20 км, спортсмен пробегает ее за 2ч. Расстояние до финиша у является функцией времени бега х . Задайте эту функцию формулой.
1) у = 20 - 10х; 2) у=20 - 2х; 3) у=10х – 20; 4) у = 20 -10/х.
9.График какой из приведенных ниже функций изображен на рисунке?
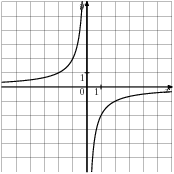
1.
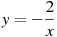
2.
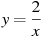
3.

4.
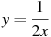
10.Постройте график функции у = 3х2 – х + 5. Укажите наименьшее значение этой функции.
11.Вычислите координаты точек пересечения параболы у = х2 + 3х – 4 и гиперболы у = 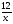
Обобщающая тестовая работа.

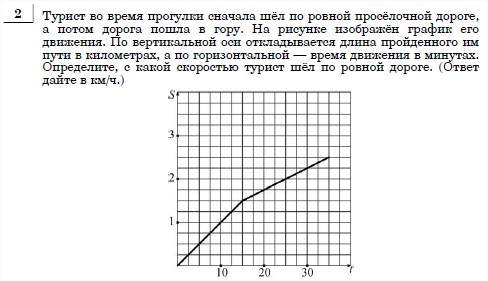


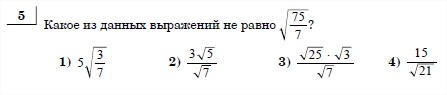
6 Геометрическая прогрессия задана несколькими первыми членами:
1; –2; 4; ... Найдите сумму первых пяти её членов.
Ответ: ___________________________.

8 Решите неравенство 4x2 + 3 + 7x < 0 .
1)(-1, - 0,75); 2) (-∞;-1)U(-0,75;+∞); 3) (-∞;-1); 4) (-0,75;+∞).
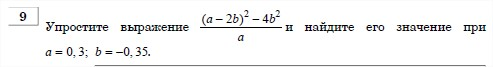
10 Из физической формулы P = I 2R выразите переменную I (все величины
положительны).
11 Из объявления фирмы, проводящей обучающие семинары:
«Стоимость участия в семинаре — 3000 р. с человека. Группам от организаций
предоставляются скидки: от 3 до 10 человек — 5%; более 10 человек — 8%».
Сколько рублей должна заплатить организация, направившая на семинар группу из 8 человек?
Ответ: ___________________________.

14 Для каждой арифметической прогрессии, заданной формулой n-го члена, укажите ее разность d.
А) аn= 4n + 3; Б) bn = 2n + 4; В) сn=3n – 2;
1) d = -2; 2) d = 4; 3) d = 2; 4) d = 3.
А
Б
В
Ответ:
15 Функции заданы формулами: А) у = х2 – 4; Б) у = - х2 + 3; В) у = - х2.
Какие из этих функций имеют наибольшее значение?
А,Б,В; 2) только А; 3) Б и В; 4) только Б.
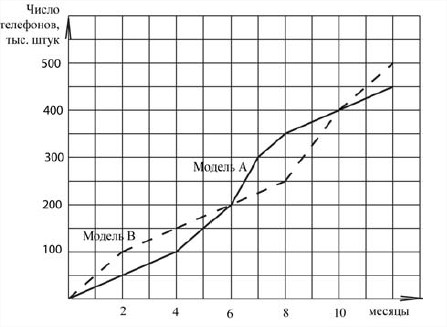
16 Фирма «Связь» выпустила в продажу две новые модели телефонов – модель А и модель В. На графиках показано, как эти модели продавались в течение года. (По горизонтальной оси откладывается время, прошедшее с начала продаж – в месяцах, а по вертикальной – число телефонов, проданных за это время – в тыс. шт.). На сколько телефонов модели В было продано больше, чем телефонов модели А за первые 4 месяца года? Ответ дайте в тыс. штук.
При выполнении заданий 17 – 19 запишите решение.
17 Сократите дробь 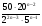 .
.
18 Решите систему уравнений 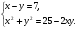
19 Найдите сумму отрицательных членов арифметической прогрессии: -10; -9,8;… ?
Используемая литература.
Алгебра: сборник заданий для подготовки к государственной итоговой аттестации в 9 кл./Л.В. Кузнецова и др. – М.:Просвещение, 2009.
ГИА 2010. Математика. Сборник заданий: 9 класс/М.Н. Кочагина, В.В. Кочагин. – М.: Эксмо, 2010.
ГИА 2010. Алгебра: тематические тренировочные задания. 9 класс/Л.В. Кузнецова и др. – М.: Эксмо, 2010.
Открытый банк заданий по математике: mathgia.ru:8080›or/gia12/