Разработка урока
алгебры по теме:
«Арифметическая
прогрессия»
Автор: учитель математики
Байтемирова Клара Низамуттеновна
с.Пресногорьковка
2014
Тип урока: урок обобщения и систематизации знаний.
Образовательные цели: создание условий на уроке для проверки и коррекции знаний, умений и навыков учащихся, связанных с решением задач по теме "Арифметическая прогрессия";
решения задач с использованием межпредметных связей;
преодоления в сознании учащихся представлений об оторванности данного материала от жизни и практики.
Развивающие цели: способствовать развитию исследовательских навыков учащихся, умений анализировать полученные данные и делать выводы;
умений осуществлять самопроверку и взаимопроверку, работу в группах;
внимания, зрительной памяти, математически грамотной речи, логического мышления, сознательного восприятия учебного материала.
Воспитательные цели:
формирование таких качеств личности, как ответственность, организованность, честность, дисциплинированность;
воспитание культуры общения, культуры диалога.
Задачи учителя на уроке:
проконтролировать знания основных формул арифметической прогрессии;
оценить умения решать ключевые задачи по данной теме;
проверить навыки учащихся по применению своих знаний в ходе решения нестандартных задач;
развить представления учащихся об использовании арифметической прогрессии в окружающей их жизни;
продолжить работу над развитием логического мышления, умением анализировать, сопоставлять и обобщать полученные знания.
Мотивация: мотивировать учащихся к осознанному восприятию и значимости материала для подготовки к контрольной работе и итоговой аттестации.
Задачи учащихся на уроке:
устранить пробелы в знаниях;
подготовиться к успешному решению контрольной работы;
применять знания в нестандартной ситуации (решение задач прикладного содержания).
Оборудование и материалы: мультимедийный проектор, индивидуальные конверты учащихся, индивидуальные карточки оценки работы ученика, карточки проверки знания формул, проверочная работа с кодированным ответом (по вариантам).
Все карточки смотреть в ПРИЛОЖЕНИИ.
Формы организации урока: фронтальная, индивидуальная, в парах, групповая.
Метод обучения: частично - поисковый, установление связи теоретических и практических знаний.
Методы ведения урока:
преобразовательный (при усвоении учащимися и творческом применении навыков и умений в процессе практической деятельности);
контрольный (при выявлении качества усвоения знаний, умений и навыков и их коррекция в процессе выполнения учащимися практических заданий);
методы стимулирования и мотивации, долга и ответственности;
методы наблюдения, сравнения, мини - диалога, самостоятельной работы, применения ТСО, наглядности;
нетрадиционные методы: самоанализа (применение взаимо - самоконтроля), личностного подхода (вселяется уверенность в свои силы).
ХОД УРОКА
I.Организационный этап.
Ознакомление учащихся с целью и задачами урока, инструктаж учащихся по организации работы на уроке.
Эпиграф урока: (мультимедийный проектор)
Желаю работать, желаю трудиться,
Желаю успехов сегодня добиться.
Ведь в будущем всё это вам пригодится.
И легче в дальнейшем вам будет учиться (слайд № 2)
II. Проверка знаний фактического материала и умение раскрывать элементарные внешние связи в предметах и явлениях. (слайд № 3)
Учащимся предлагается заполнить таблицу.
Арифметическая прогрессия аn
1. Определение
2. Формула n-первых членов прогрессии
3. Сумма n-первых членов прогрессии
4. Свойства
Проверка формул.
Через 5 минут на экране появляются формулы арифметической прогрессии. Ученики проверяют формулы. (Слайд №4)
Арифметическая прогрессия аn
1. Определение
an+1= an +d
2. Формула n-первых членов прогрессии
an=a1 + d(n-1)
3. Сумма n-первых членов прогрессии
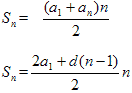
4. Свойства
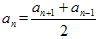
Самооценивание.
III. Устная работа:
Цель: проверить ЗУН по теме: «Прогрессии.
Метод: фронтальный опрос.
Задание: (Слайд №5)
1. Дать формулу n-го члена последовательности
1,2,3,4,5, . . . Ответ: n
1,4,9,16,25, . . . Ответ: n2
1,8,27,64,125, . . . Ответ: n3
2. Вычислить первые три члена последовательности: (Слайд №6)
An=4n-1
А1=3, А2=7, А3=11
Вn= -5n+4
В1= -1, В2= -6, В3= -11
Сn=-n
С1=-1, С2=-2, С3=-3
Самооценивание.
IV. Обратимся к страницам истории. (Слайд №7)
“Пусть властно по своей орбите нас ритм сегодняшний кружит – Вернее будущее видит лишь тот, кто прошлым дорожит”
Хочу рассказать вам об одном интересном эпизоде из жизни немецкого математика К.Ф.Гаусса (1777-1855).
Когда ему было 9 лет, учитель, стремясь надолго занять детей, задал на уроке следующую задачу.
“Сосчитать сумму всех натуральных чисел от 1 до 40”
На удивление учителя один из учеников (это был Гаусс) через минуту воскликнул: “Я уже решил”. В тетради Гаусса было только одно число, но зато верное.
Ребятам предлагается решить туже самую задачу, ведь 9 – летний Гаусс с ней справился. Рассуждения Гаусса – как проверка. (Слайд №9)

Решаем у доски.
Страницы Российской истории.
В первом учебнике “ Арифметика” Магницкого (конец 18 в.) имеется значительное количество задач на прогрессии. Приведем пример задачи аналогичной тем, что упоминаются в математическом учебнике. (Слайд №10)
“ Некто продавал коня. Просил за него 25 рублей. Пожелавший купить купец возмутился, что дорого. “Хорошо, - ответил продавец. Бери коня даром, а заплати только за гвозди на его подковах. А гвоздей во всякой подкове 6 штук. И будешь ты мне платить за них таким образом: за первый гвоздь 10 копеек, за второй гвоздь 20 копеек, за третий – 30 копеек и т.д.” Купец же, думая, что заплатит намного меньше, чем 25 рублей, согласился. Проторговался ли купец, и если да, то на сколько?”
Решение
А1=10,А2=20, А3=30,…А24=240
Сумма=(10+240)/2*24=250*12=3000=30рублей
Эту задачу решаем у доски.
Страницы современной школы. 1 группа (Слайд №11)
Задача 1 (физическая). "Свободно падающее тело проходит в первую секунду 4,9 м, а в каждую следующую секунду на 9,8 м больше, чем в предыдущую. Найдите глубину шахты, если свободно падающее тело достигло дна шахты через 5 секунд после начала падения".
Решение:

Ответ: глубина шахты 122,5 м.
Для 2-ой группы (Слайд №12)
Задача 2 (от строителя). При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основание положить 12 бревен?
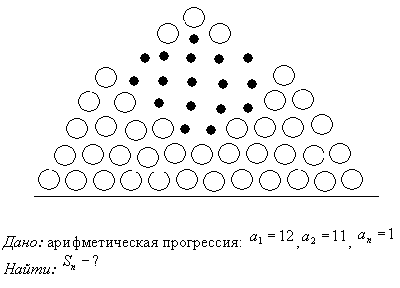
Решение:

Ответ: 78 бревен в одной кладке.
Задача 3 (Задача от будущего медика). 3 группа (Слайд №13)
Курс воздушных ванн начинают с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин?
Решение: Имеем арифметическую прогрессию а1=15, d=10, аn=105. Найти n.Решение:аn=a1 +(n-1)*d105=15+(n-1)*10105=15+10n-1010n=100n=10 Ответ: 10 процедур.
VII. Домашнее задание: (Слайд № 14)
а)Творческое: найти задачи, связанные с арифметической прогрессией из различных областей: физики, медицины и т.д.
б) Решить задачи на прогрессию из сборника по подготовке к ВОУД (по вариантам)
VIII. Итог урока.
В течение урока мы повторили основные формулы арифметической прогрессии.
Показывали применение этих формул в стандартных и нестандартных ситуациях, тем самым вели подготовку к контрольной работе и успешной сдачи итоговой ВОУД.
Что для вас наиболее значимым было на уроке?
Что у вас вызвало интерес?
Заключение: на мультимедийном проекторе (Слайд № 15)
"Да, путь познания не гладок,
Но знаем мы со школьных лет,
Загадок больше, чем разгадок
И поискам предела нет".
Желаю вам успехов в ваших дальнейших поисках!
Теоретически – практический тест
Вариант 1
Бесконечно упорядоченный набор чисел
а) порядок б) последовательность в) номер
2. Последовательность обозначается
а) аn б) аn в) ( аn )
3. Числа, образующие последовательность, называются:
а) членами б) номерами в) числами
4. Члены последовательности обозначаются:
а) а1, а2, а3,… б) 1а, 2а, 3а,… в) а1, а2,а3,….
5. Последовательности бывают:
а) параллельные б) конечные в) бесконечные
г) колеблющиеся д) постоянные е) квадратные
6. Способы задания последовательностей:
а) формулой n – го члена б) уравнением
в) рекуррентный способ г) словесно
7. Найдите первые 3 члена последовательности, заданной формулой n – го члена хn = 2n – 1
а) 2; 7; 8;… б) 1; 3; 5; … в) -1; 2; 6; …
8. Найдите седьмой член последовательности
( аn), заданной формулой: аn = n( n + 1 )
а) 5 б) 12 в) 56
9. Найдите второй член последовательности ( сn ),
если с1 = 8; сn+1 = cn – 1
а) 6 б) 7 в) 8
10. ( аn) – последовательность квадратов натуральных чисел. Выпишите первые 3 её члена.
а) 1; 4; 9; … б) 1; 2; 3; …. в) 1; 5; 12; …
Вариант 2
1. Способы задания последовательностей:
а) формулой n – го члена б) уравнением
в) рекуррентный способ г) словесно
2. Последовательности бывают:
а) параллельные б) конечные в) бесконечные
г) колеблющиеся д) постоянные е) квадратные
3. Члены последовательности обозначаются:
а) а1, а2, а3,… б) 1а, 2а, 3а,… в) а1, а2,а3,….
4. Числа, образующие последовательность, называются:
а) членами б) номерами в) числами
5. Последовательность обозначается
а) аn б) аn в) ( аn )
Бесконечно упорядоченный набор чисел
а) порядок б) последовательность в) номер
7. ( аn) – последовательность квадратов натуральных чисел. Выпишите первые 3 её члена.
а) 1; 4; 9; … б) 1; 2; 3; …. в) 1; 5; 12; …
8. Найдите второй член последовательности ( сn ),
если с1 = 8; сn+1 = cn – 1
а) 6 б) 7 в) 8
9. Найдите седьмой член последовательности
( аn), заданной формулой: аn = n( n + 1 )
а) 5 б) 12 в) 56
10. Найдите первые 3 члена последовательности, заданной формулой n – го члена хn = 2n – 1
а) 2; 7; 8;… б) 1; 3; 5; … в) -1; 2; 6; …
(учащиеся выполняют тест по вариантам, при проверке обмениваются тестами и выполняют взаимопроверку по предложенным ответам, выставляют оценки согласно критериям.)
Ответы: (Слайд 16)
В1: 1.б; 2.в; 3.а; 4.в; 5.б,в; 6.а,в,г; 7.б; 8.в; 9б; 10.а
В2: 1.а,в,г; 2.б,в; 3.в; 4.а; 5.в; 6.б; 7.а; 8.б; 9 .в; 10.б
Дополнительное задание:
Решите задачу: условия задачи на мультимедийном проекторе, там же и доказательство.
Найдите: (Слайд №17)
а) сумму 2 + 4 + 6 + : + 2n, слагаемыми которой являются все четные натуральные числа
от 2 до 2n;
Решение. (Слайд № 18)
Найдите: (Слайд № 19)
б) сумму 1 + 3 + 5 + : + (2n - 1), слагаемыми которой являются все не четные числа
от 1 до 2n - 1.
Решение. (Слайд № 20)