Решение задач по механике с использованием тригонометрии, 10 класс

Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа № 34 города Томска

Конспект интегрированного урока по алгебре и физики в 10 классе«Решение задач по механике с использованием тригонометрии»

Подготовили:

учитель математики

Пихтовникова Светлана Александровна,

Учитель физики

Бурлаков Алексей Дмитриевич

Томск 2010

«Решение задач по механике с использованием тригонометрии»

Интегрированный урок для профильного физико-математического класса.

10 класс.

Пихтовникова Светлана Александровна,

учитель математики

высшей категории,

Бурлаков Алексей Дмитриевич,

Учитель физики

МОУ СОШ № 34 города Томска

     Наука начинается тогда,когда начинают считать. Д.И.Менделеев

Слеп физик без математики. М.В.Ломоносов

Рано или поздно всякая

правильная математическая идея

находит применение в том

или ином деле.

А.Н.Крылов

Цель урока:

Закрепление и актуализация, и интеграция знаний по физике и математики.

Задачи урока:

1. Образовательные задачи:

   • Закрепить знания обучающихся по теме: «Механика», тригонометрические формулы и решение тригонометрических уравнений;

   • Продолжить формирования навыков решения задач, формировать умение решать нестандартные задачи

   • Показать на наглядном примере связь тригонометрии и механики.

2. Развивающие задачи:

   • Развитие логического мышления, актуализировать имеющиеся знания в новой нестандартной ситуации

3. Воспитание учащихся на уроке:

   • НОТ: обучение умению ставить цель, выделять существенное, главное, планировать работу, осуществлять самоконтроль, подводить итоги, работать в оптимальном темпе, беречь время.

Тип урока: интегрированный урок – практикум.

Оборудование: мультимедийный проектор, ватман, чертежные инструменты, математическая энциклопедия, раздаточный материал.

План урока:

1. Организационный момент. Вступительное слово учителя

2. Устная разминка

3. Работа по группам

4. Защита работ

5. Историческая справка

6. Практическая работа

7. Итог урока. Заключительное слово учителя.

Ход урока:

1. Вступительное слово учителя. Слайды: 2,3,4

Начало тригонометрии 10 класса.

2. Устно:

1. Вспомним формулы (Слайд 5)

• Уравнение скорости:

• Перемещение при равноускоренном движении:

• Тело брошено под углом к горизонту. Дальность полета, высота полета:

• (дальность)

• (высота)

• Формула для нахождения силы трения: (Слад 6)

• Закон сохранения импульса:

• Закон сохранения механической энергии(без учета трения)

• Найдите сторону х прямоугольного треугольника, изображенных на данных рисунках (Слайды7,8,9,10)

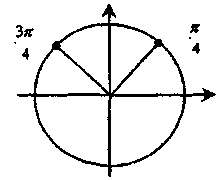
Выберите тригонометрическое уравнение, решения которого включают обе точки, отмеченные на единичной окружности. (Слайд 11)

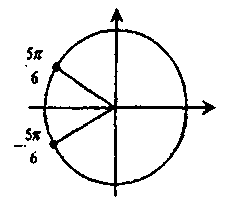
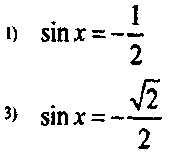
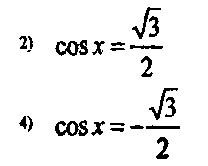
Выберите тригонометрическое уравнение, решения которого включают обе точки, отмеченные на единичной окружности. (Слайд 12)

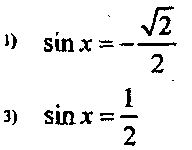
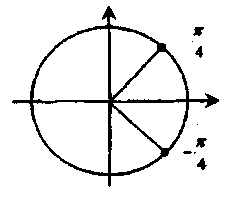
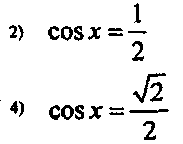
Выберите тригонометрическое уравнение, решения которого включают обе точки, отмеченные на единичной окружности. (Слайд 13)

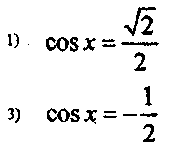
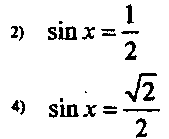
3. Работа по группам.

Каждой группе выдаются ватманы, задания, фломастеры, математическая энциклопедия.

Свой отчет о работе учащиеся оформляют на листах ватмана

1 группа (Слайд 14)

1.Под каким углом нужно бросить мяч , чтобы он улетел как можно дальше?

2. в справочнике найдите, что означает тригонометрия

2 группа (Слайд 15)

1. Летящая пуля ударяет в шар висящий на невесомой, нерастяжимой нити, ударяет и застревает в нем. Длина нити 1 м, m_пули =9г, m_шара= 9 кг, угол на который отклоняется шар с пулей 10⁰. Найти скорость летящей пули.

2. в справочнике найдите, что означает синус

3 группа (Слайд 16)

1. Найдите коэффициент трения между шариковой ручкой и бумагой.

Оборудование: линейка.

Силой тяжести ручки можно пренебречь.

2. в справочнике найдите, что означает косинус

4 группа.

1. Решите уравнение:

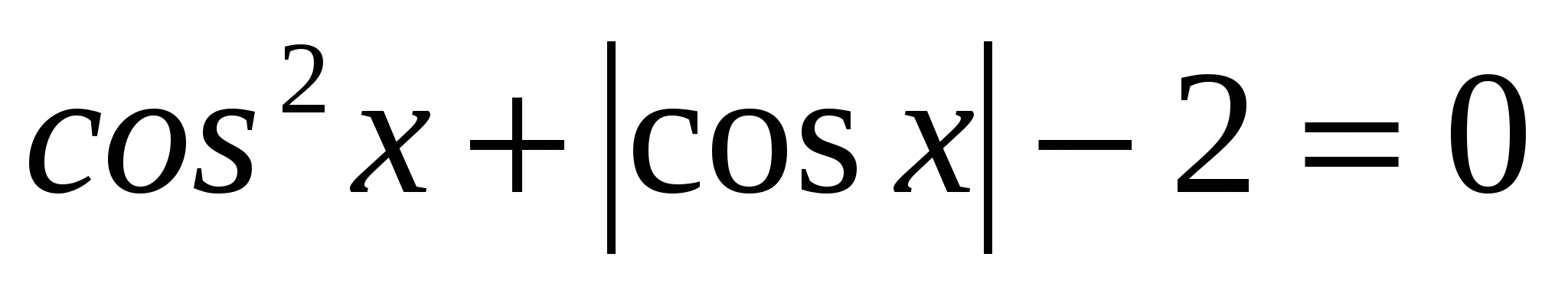
2. в справочнике найдите, что означает тангенс

5 группа.

1. Решите уравнение с параметром а:

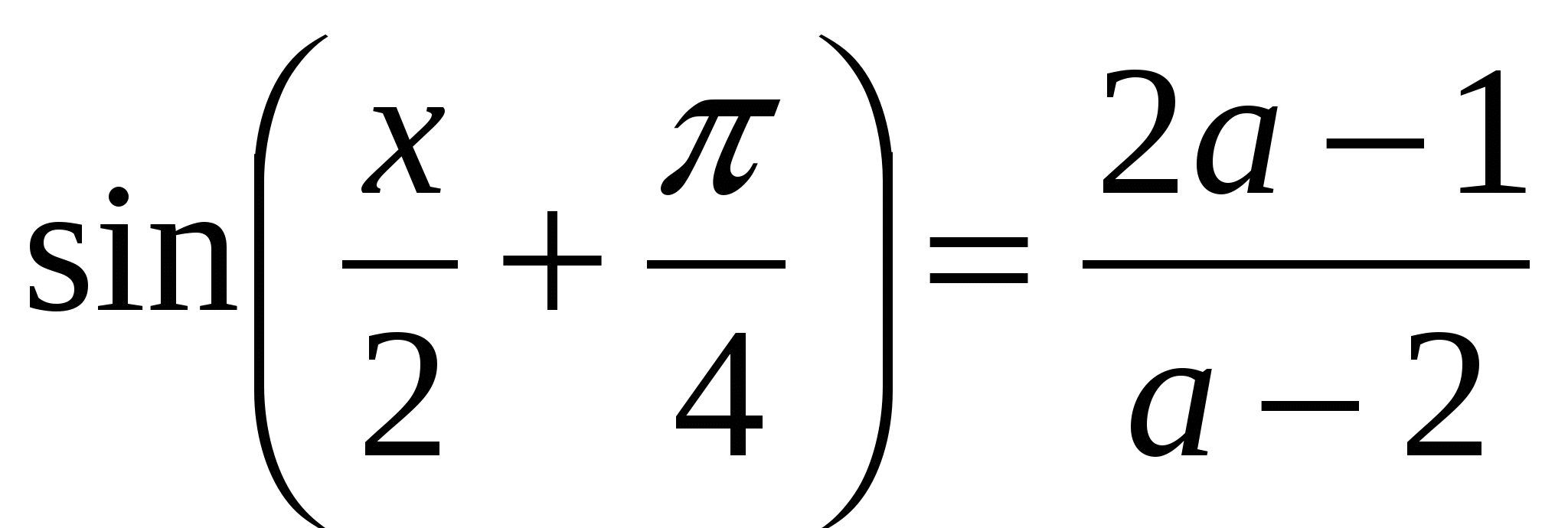
2. в справочнике найдите, что означает котангенс

4. Отчет групп сопровождается показом рисунков на экране (слайды 14-17)

Задача 1.

Под каким углом к горизонту нужно бросить мяч, чтобы он упал максимально далеко?

Y

_

А υ

_

υ_{0 _}

g

h

α

O X

l

Движение мяча можно описать в двухмерной системе координат, где движение вдоль оси ОХ – равномерное, а вдоль оси ОY – равноускоренное с ускорением g = 9,8м/с², t_п – время полета,

l - υ₀ cos α • t_п , дальность полета 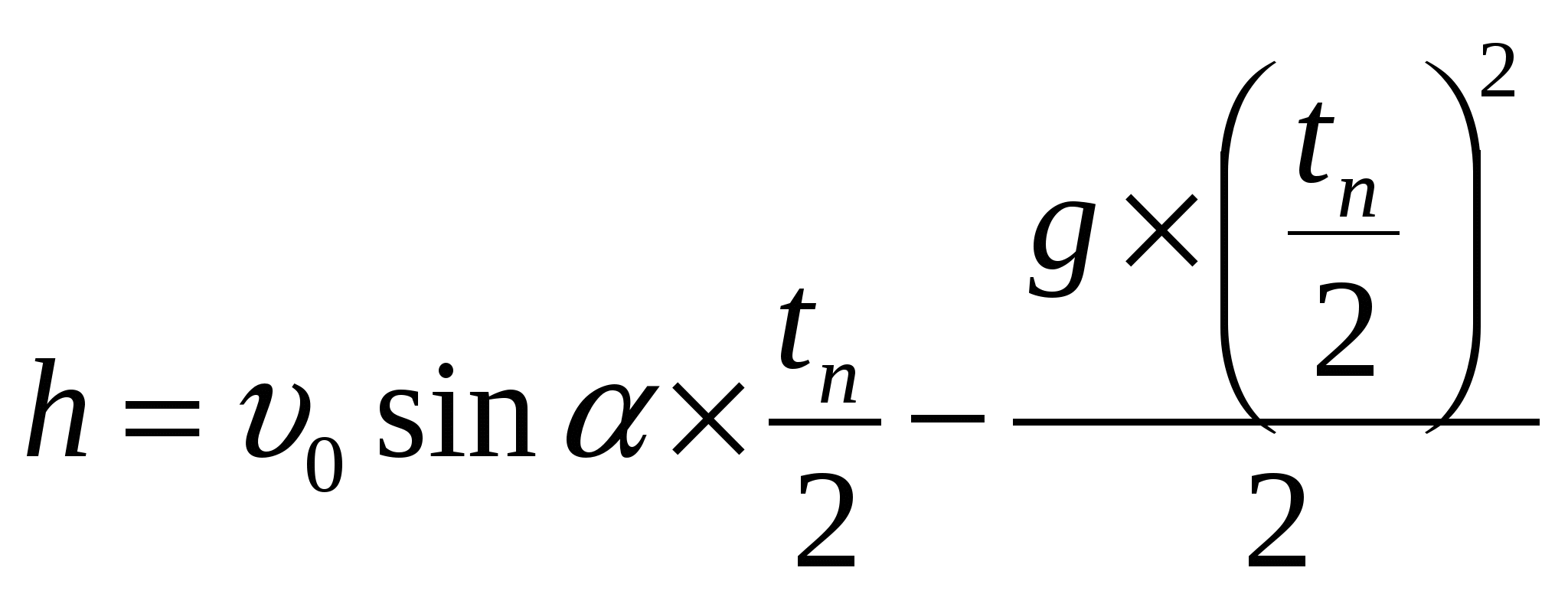- максимальная высота полета

в точке А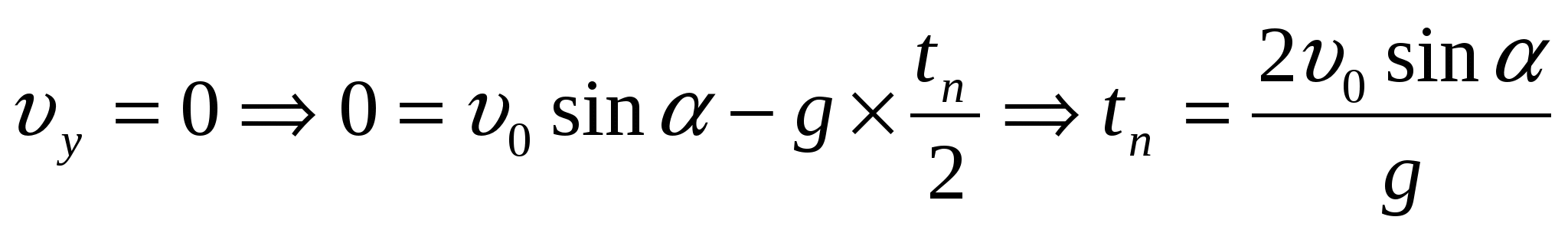

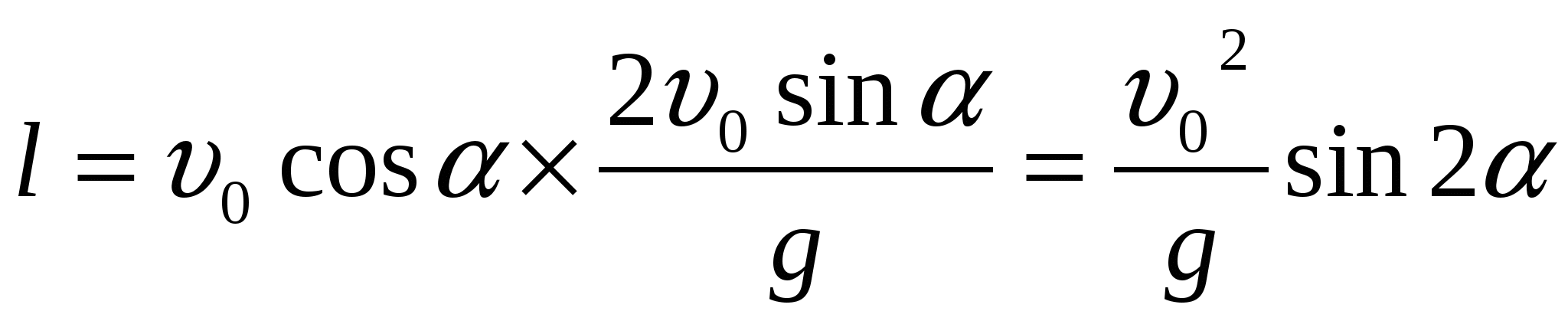
так как 2 sinα cosα = sin2α  l max когда sin 2α = 1  sin 2α = 1; 2α = 90; α = 45, то есть мяч надо бросить под углом 45 к горизонту и дальность полета будет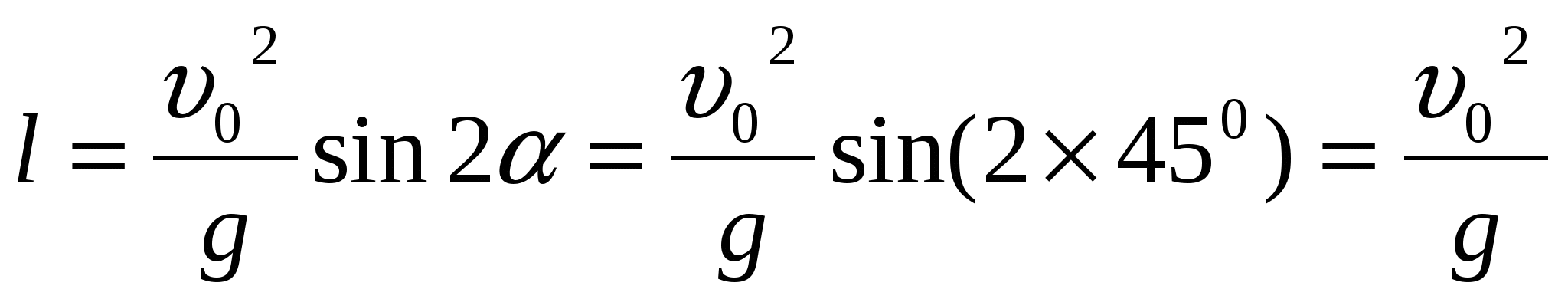

Задача 2. (Слайд 15)

С какой скоростью υ₁ должна лететь пуля, чтобы после абсолютно неупругого удара она отклонила шар, подвешенный на нити, на угол α? Масса пули m₁ , масса шара m₂, длина нити l ,угол отклонения α.

Закон сохранения импульса для пули и шара в проекциях m₁ υ₁= (m₁ + m₂)υ где υ – скорость пули и шара после удара, 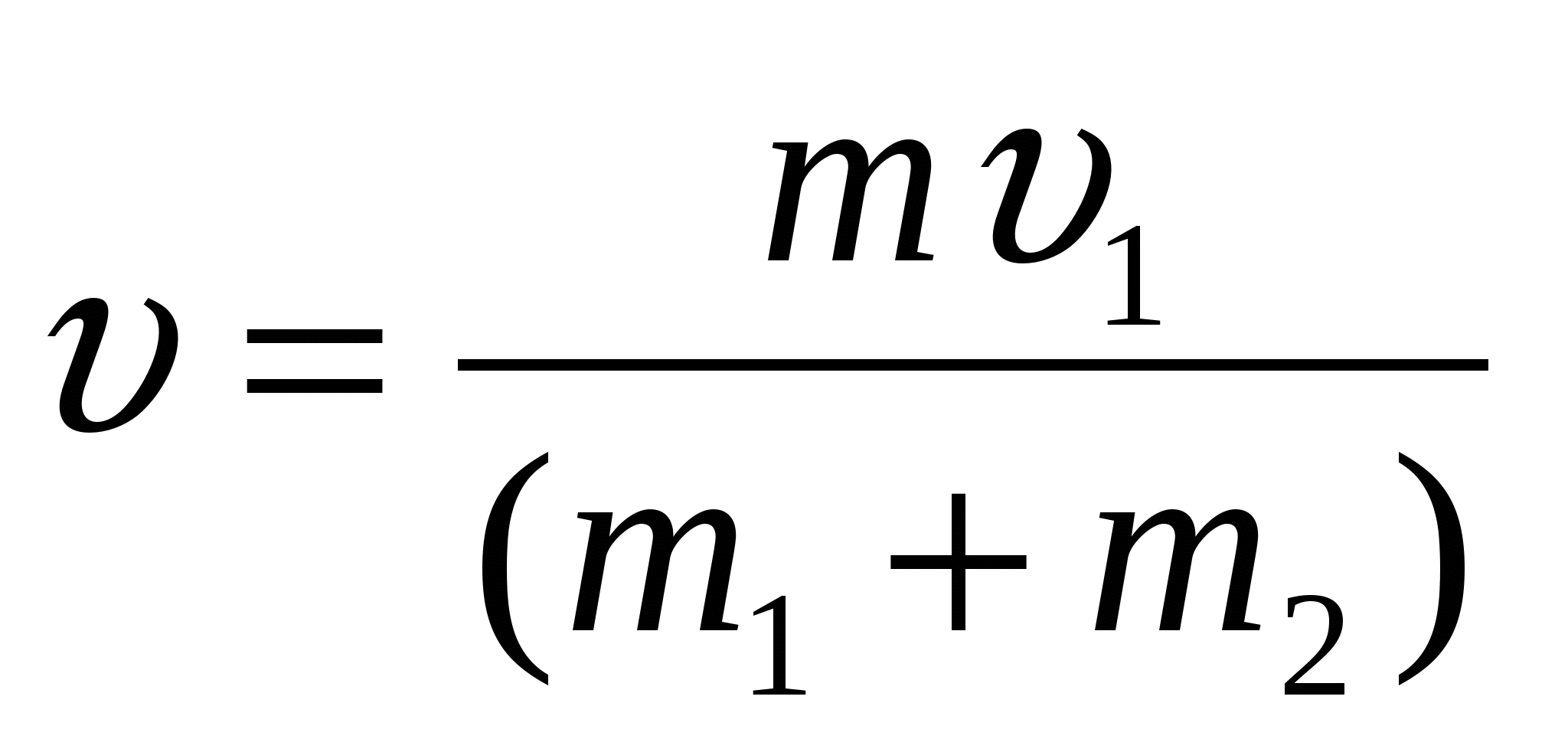(1)

Закон сохранения энергии для пули и шара, отклонившихся на угол α после удара, где h – высота подъема пули и шара после удара

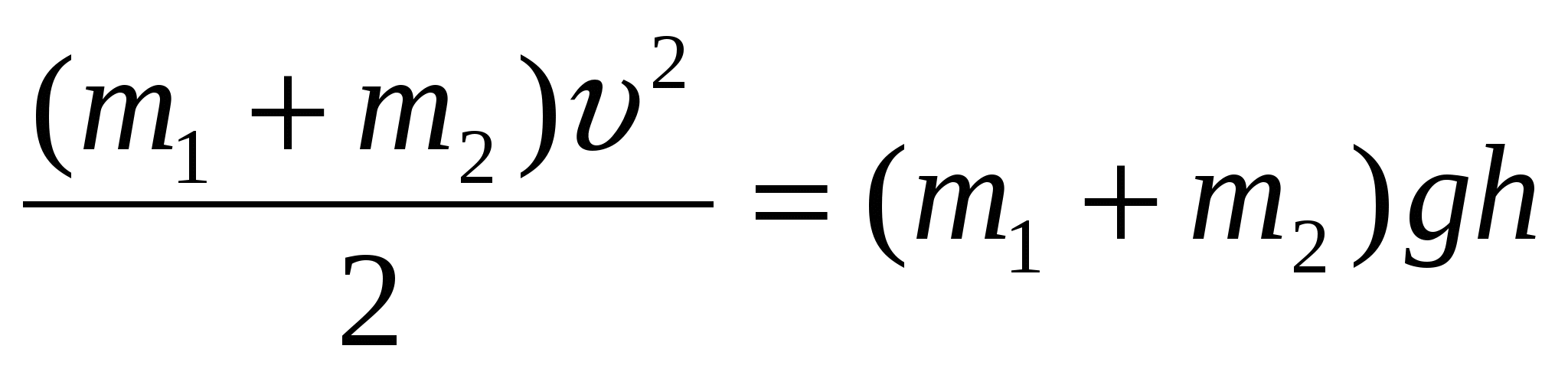
h = l – l cosα = l (1-cosα)  υ²=2gl(1-cosα) подставляя формулу (1) получаем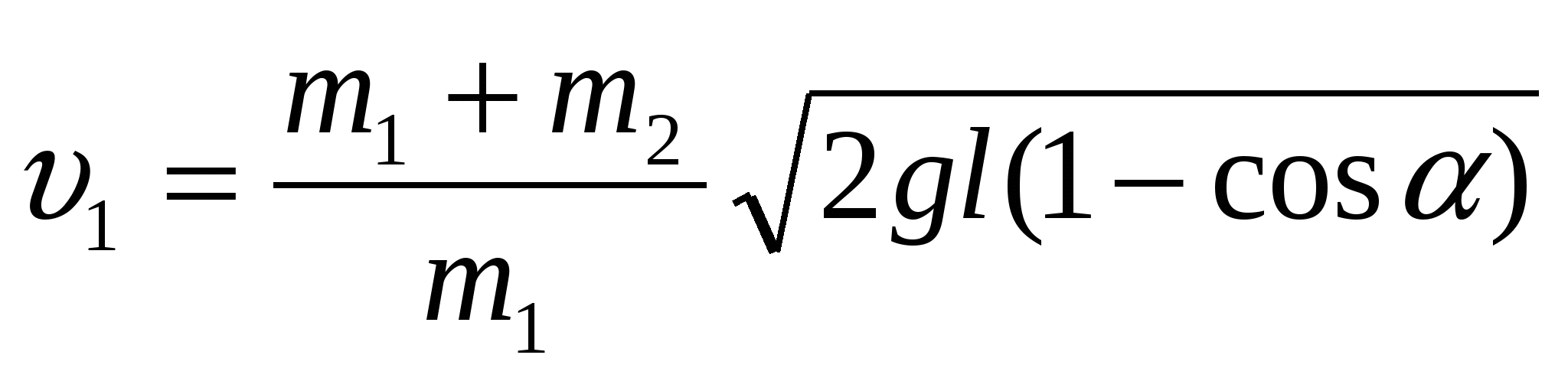, используя 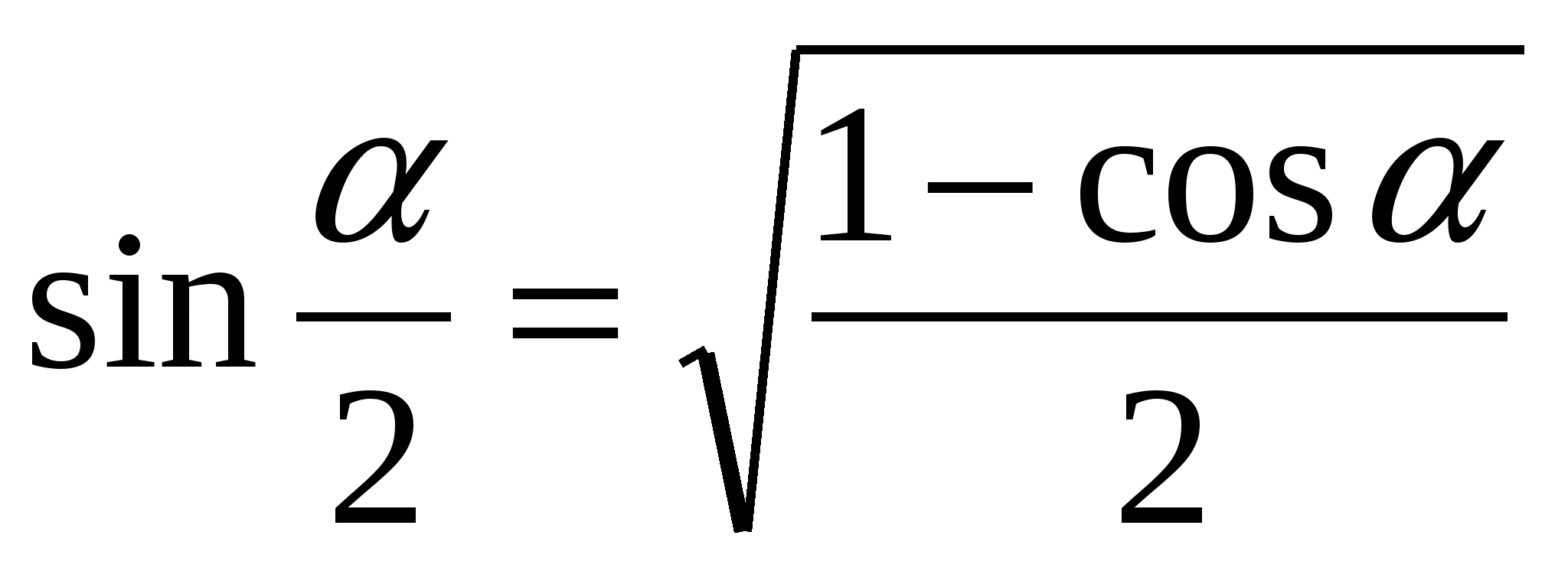, получаем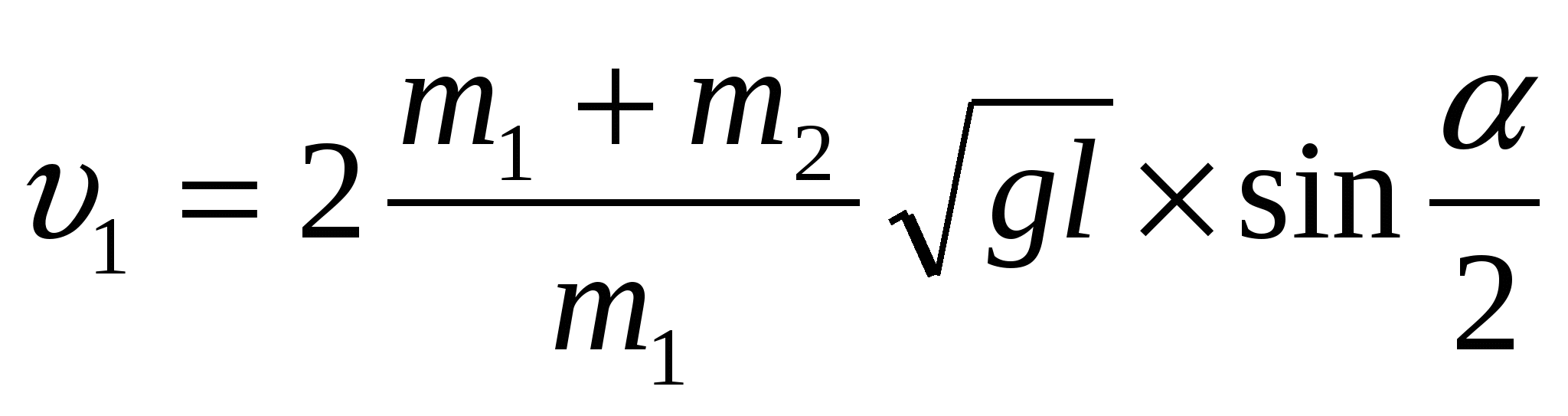

Задача 3.(Слайд 16)

Найдите коэффициент трения между ручкой и бумагой (массой ручки пренебрегите). Укрепитесь в бумагу вертикально поставленной ручкой, а затем постепенно наклоняйте ее, продолжая нажимать на верхний конец. При некотором угле наклона α ручка начнет скользить по бумаге. Это произойдет в тот момент, когда горизонтальная составляющая силы F станет больше максимальной силы трения покоя между ручкой и бумагой.

В момент начала скольжения Fcosα = (mg + Fsinα) где m – масса ручки.  = Fcosα /(mg + Fsinα)

Масса ручки невелика, сила F ограничена только возможностями экспериментатора и прочностью ручки, поэтому массой ручки можно пренебречь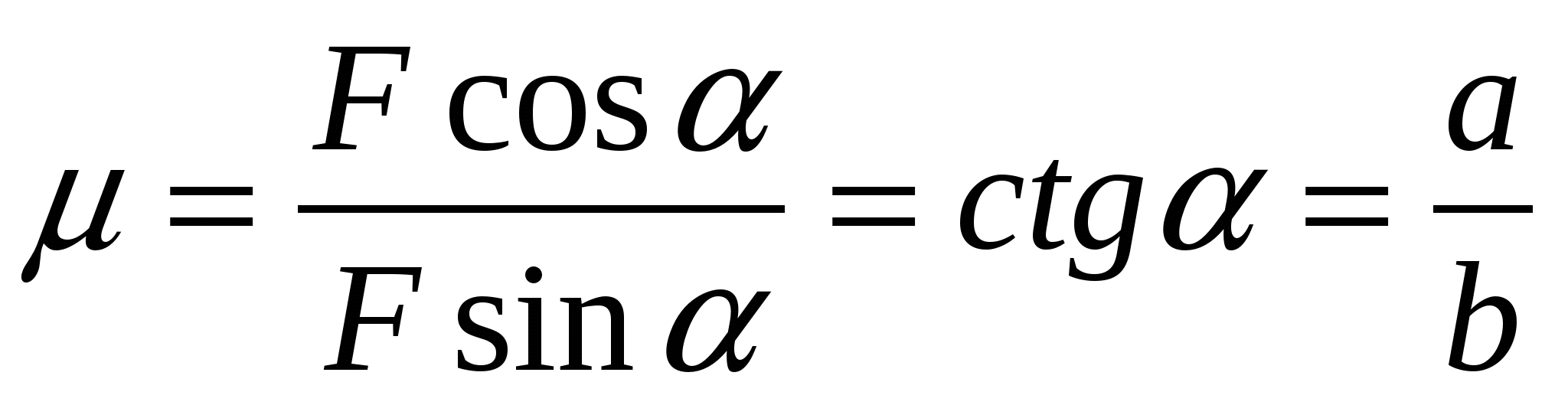

5. Немного истории:

«Кто впервые придумал рассматривать изу­чаемое математическое понятие и зачем?».

Впервые тригонометрические соотношения вводятся в курсе геометрии следующим образом. Рас­сматривается прямоугольный треугольник (рис. 1), и на уровне определений утверждается: (Слайд18)

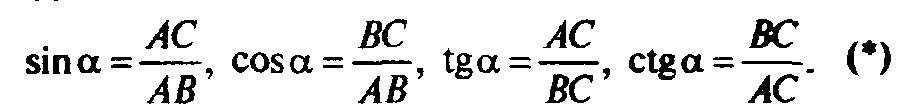
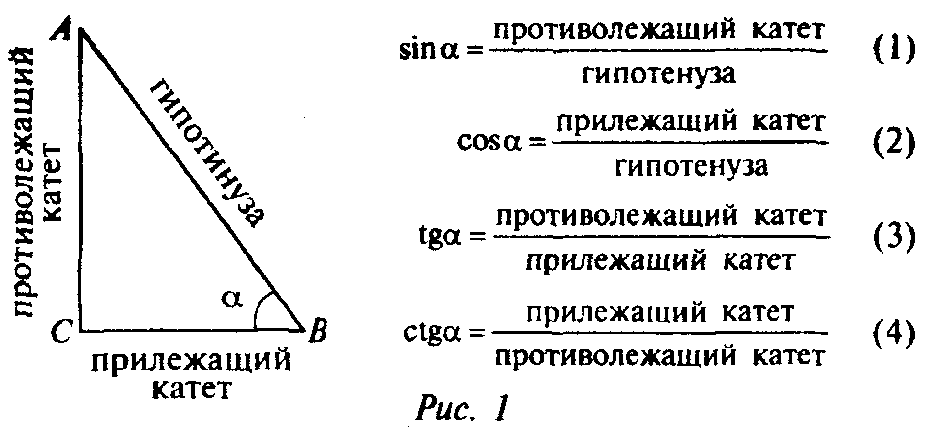
В первую очередь нас будут интересовать вопро­сы: «Откуда появилась необходимость рассматри­вать представленные выше соотношения сторон прямоугольного треугольника?» и «Как появилась символика, используемая в определениях (*)?».

Ключ к отгадке надо искать в практической де­ятельности людей, причем речь идет о временах настолько далеких (может второе тысячелетие до н.э., а может и ранее), что никакими письменными свидетельствами, позволяющими дать однозначный ответ, мы не располагаем. Поэтому позволим себе высказать некоторые догадки.

В древние времена строительство сооружений велось примерно таким образом и такими средст­вами, как и сегодня строят небольшие дома и под­собные помещения. При этом строители использу­ют нехитрые инструменты: веревку, отвес, колыш­ки и пр. Между прочим, в Древнем Египте сущест­вовали люди специальной профессии, которых на­зывали гарпедонапты, что значит, натягиватели веревки. С них начиналось любое строительство. А зачем нужна веревка строителям? Чтобы ровно в линию выкладывать кирпичи или камни.

Предложим учащимся вслушаться в слова «ли­ния» и «лен». Действительно, откроем этимоло­гический словарь:

Линия. Через посредство немецкого языка заим­ствовано в начале XVIII в. из латыни. Лат. linea -«нитка» — производное от linum — «лен». Еще веревка нужна для того, чтобы получить прямой угол, например в целях строительства при­вычного нам четырехугольного дома. Ведь такой дом построить легче всего. А строительство домов иных форм и сейчас является трудной архитектур­ной задачей.

Учащиеся уже знают, что одним из важнейших изобретений человечества было изобретение ко­леса. А почему? Да потому, что в природе колеса нет. Колесо — это именно человеческое изобре­тение. Теперь другой вопрос: а есть ли в природе прямой угол? Примеры привести можно (ветка, растущая перпендикулярно стволу дерева; само дерево, растущее перпендикулярно к земле и т.п.), но вряд ли перечисленное годится для того, чтобы создать шаблон прямого угла. Издавна строители научились получать прямой угол с помощью веревки. В Древнем Египте заме­тили, что если на веревке завязать узелки на рав­ном расстоянии друг от друга, и натянуть веревку так, чтобы, говоря современным языком, получал­ся треугольник со сторонами 3, 4, 5, то угол, ле­жащий против наибольшей стороны, окажется пря­мым. С тех пор треугольник со сторонами 3, 4, 5 называется египетским.

Треугольник с черными кружками, обозначаю­щими узлы, показан на рис. 2. Этот чертеж лучше всего поясняет суть дела. В вершинах треугольника мы видим древние египетские изображения жре­цов. У них в руках — инструменты, напоминающие измерители расстояний, какими пользуются и сей­час. В Древнем Египте измерения были священ­ным делом - уделом немногих образованных лю­дей — жрецов.

Историю с натягиванием веревки продолжают еще несколько древних терминов: катет — значит «отвес», гипотенуза — «натянутая», а другой катет прямоугольного треугольника не назывался кате­том (т.е. отвесом), о нем говорили как об основании (рис. 3). (Слайд 19)

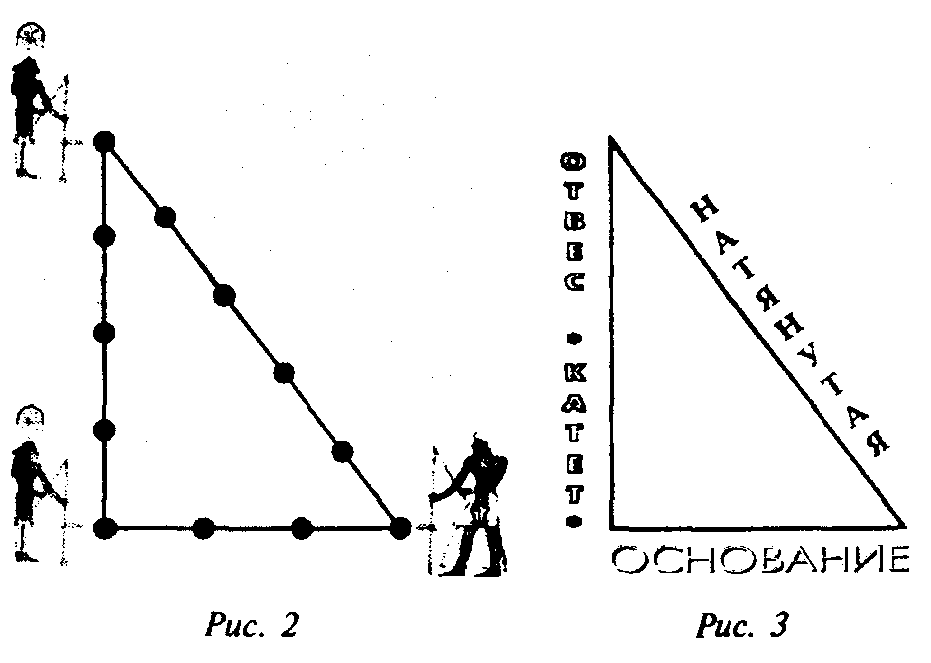
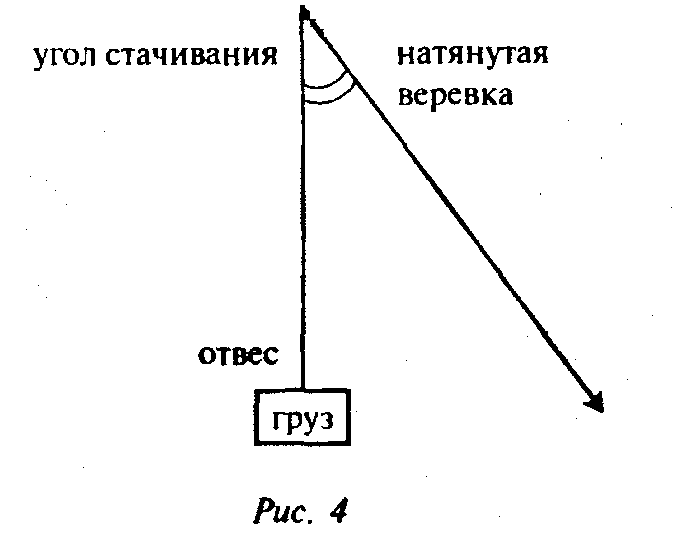
По натянутой веревке (другими словами, по ги­потенузе) можно проводить стачивание боковой грани строящейся пирамиды.

Теперь мы подошли к главному вопросу: «Как объяснить строителям, по какому углу стачивать грань пирамиды?» (В Древнем Египте пирамиду выкладывали из грубых крупных камней, и надо было ее отшлифовать или иным образом подкор­ректировать.) Один из способов: задать отношение высоты пирамиды к апофеме, или, если говорить о плоскости, задать отношение катета-отвеса к ги­потенузе. Вот и получается прообраз косинуса угла стачивания (рис. 4). А когда задавались другие от­ношения — отношение катета-основания к катету-отвесу или отношение катета-основания к гипоте­нузе — это были прообразы понятий тангенса и синуса угла.

(Слайд 20)

В самом деле, задавать указанные отношения сторон прямоугольного треугольника очень удоб­но. Так, если на макете пирамиды (рис. 5, а) опре­делить отношение высоты пирамиды к ее апофеме как 2:3, то и для самой пирамиды (рис. 5, 6) это отношение сохранится, ведь большая пирамида есть подобие маленькой (макета пирамиды). (Слайд 21)

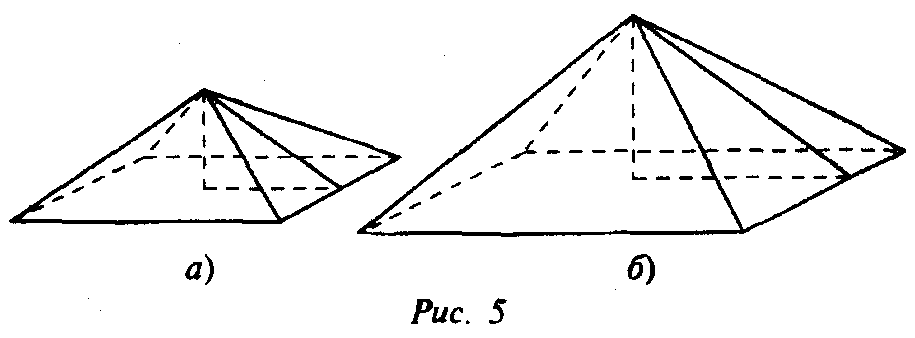
Теперь мы понимаем: рассматривать отношения длин строи прямоугольного треугольника очень удобно, так как для всех подобных прямоугольных треугольников эти отношения сохраняются (все правильно, как потом узнают учащиеся, у подоб­ных треугольников углы равны, а, значит, равны и тригонометрические функции углов).

Судя по всему, на идею подобных фигур люди обратили внимание достаточно давно. Одинаковые по форме, но различные по величине фигуры встре­чаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадра­тиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров (сво­его рода «палетка»).

В дальнейшем геометрические знания накапли­вались, а тригонометрические соотношения в пря­моугольных треугольниках стали все чаще исполь­зоваться для решения таких задач практики, как нахождение расстояний до недоступных объектов. Приведем несколько примеров.

Легенда гласит, что Фалес (философ и матема­тик, имя которого уже известно учащимся) привел в изумление египетского царя Амазиса, измерив высоту одной из пирамид по величине отбрасыва­емой ею тени. Догадка Фалеса заключалась в том, что в течение дня бывает момент, когда длина тени каждого предмета равна высоте самого этого пред­мета. Он дождался момента, когда длина его тени стала равна его росту, и тогда, измерив тень пира­миды, вычислил ее высоту. Сформулируем другую не менее известную задачу:

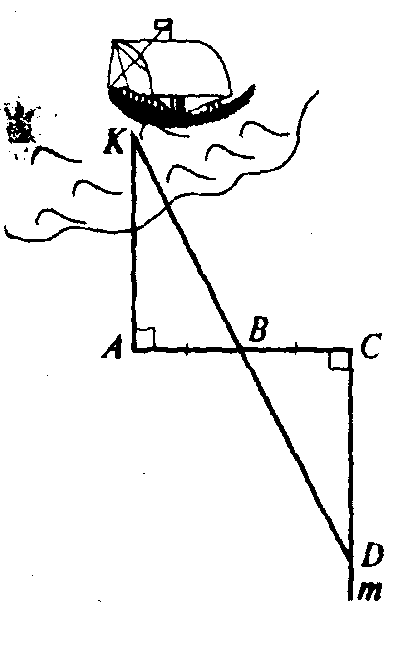
Задача 1. Определить расстояние от корабля, находящегося в море, до берега (Слайд 22)

Решение. Пусть корабль находится в точке К, а наблюдатель - в точке А (рис. 6). Построим прямой угол с вершиной в точке А, откладыва­ем на берегу отрезок АС и делим его пополам точкой В. Затем из точки С передвигаемся по прямой т, перпендикулярной ВС, до тех пор, пока не дойдем до точки D, из которой точки К и В видны лежащими на одной прямой. Отме­тим полученную точку как D. Прямоугольные треугольники BCD и ВАК рав­ны, следовательно, АК = CD, а длину отрезка CD можно непосредственно измерить.

Решение задач о нахождении расстояний до не­доступных объектов, а также задач на вычисление недоступных высот было одним из источников развития тригонометрического знания. К сожале­нию, на момент рассказа об этом учитель почти ничего не может показать учащимся, так как они еще не изучали подобие треугольников, теоремы синусов и косинусов и пр. Однако позже к этим задачам можно вернуться. Поэтому мы приведем дополнительно еще одну очень известную задачу. Ее текст можно найти в трактате китайского мате­матика III в. Лю Хуэя «Математика морского ост­рова». Несколько странное название трактата объ­ясняется тем, что в нем решены различные задачи на определение расстояний до недоступных объек­тов, расположенных на острове, причем точка на­блюдения находится вне его.

Задача Лю Хуэя.

Задача 2. Наблюдают недоступный морской ос­тров (рис.).(Слайд 23)

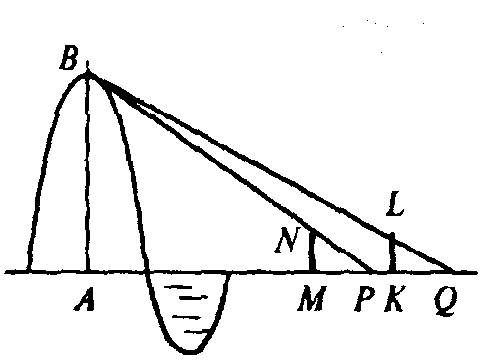
Для этого установили пару шестов MN и KL одинаковой высоты в 6 бу (6 шагов). Предыдущий шест от последующего удален на 1000 бу (Л/А). Пусть последующий шест (АХ) вместе с предыдущим (А/УУ) находится на одной прямой с островом. Если отойти от предыдущего шеста по прямой на 123 бу (МР), то глаз челове­ка, лежащего на земле, будет наблюдать верхний конец шеста совпадающим с вершиной острова

Если отойти по прямой от последую­щего шеста на 127 бу (KQ), то глаз человека, лежащего на земле, будет наблюдать верхний ко­нец шеста также совпадающим с вершиной остро­ва

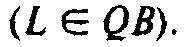
Какова высота острова (АВ) и его удаленность от первого шеста (AM).

Решение. Рассмотрим две пары подобных тре­угольников АВР, MNP и ABQ, KLQ. В совре­менных обозначениях запишем:

(*)

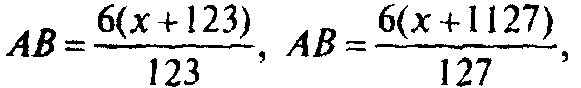где х = AM.

Приравнивая выражения для АВ, найдем

х = 30750 (бу), АВ= 1506 (бу). Заметим, что в выражениях (*) отношение

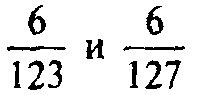
есть значения тангенсов углов NPM и

LQK, так что в манипулировании с подобными тре­угольниками уже содержатся предпосылки к пере­ходу к тригонометрическим понятиям.

До сих пор мы рассматривали самую глубинную предысторию зарождения тригонометрического знания, но именно она отразилась в самом слове «тригонометрия», которое буквально означает «из­мерение треугольника». Действительно, термин тригонометрия состоит из двух греческих слов: тригоном, что означает «треугольник» и метрейн, что означает «измерять». Кроме того, данный первич­ный исторический рассказ помогает объединить в сознании учащихся такие темы, как знакомство с прямоугольным треугольником, теорема Пифаго­ра, подобие треугольников, тригонометрические соотношения в прямоугольном треугольнике. И главное, у учащихся возникает желание посмотреть на эти темы как с исторической, так и с современ­ной точек зрения, т.е. повышается интерес к изу­чению геометрии.

Теперь мы перейдем собственно к моменту, ког­да мы можем обратиться непосредственно к исто­рии тригонометрии. Итак, тригонометрия, как и всякая наука, выра­стала из потребностей человеческой практики, поэтому потребности не ограничивались, как мы упо­минали выше, только лишь потребностями строи­тельства или нахождения расстояний до недоступ­ных объектов. Задачи мореплавания, требовавшие по звездам определять правильный курс корабля, задачи определения по звездам пути при движении караванов в пустыне, задачи земледелия, требовав­шие введения точного календаря, и многие другие обусловили развитие астрономии, а с ней и триго­нометрии. Причем сферическая тригонометрия развивалась наряду с плоской.

По сути, тригонометрия появилась в древности как один из разделов астрономии. Дело в том, что преобладающей гипотезой о строении Вселенной была геоцентрическая, согласно которой Земля есть шар, расположенный в центре небесной сферы, ко­торая равномерно вращается вокруг своей оси. Светила считаются расположенными на этой сфе­ре. При изучении их движения большое значение приобретают задачи о расположении точек и фигур на сфере. Работы, в которых подобные задачи ре­шаются, получили название сферики. Плоская три­гонометрия при таких условиях отнюдь не играла лишь второстепенную роль по сравнению со сфе­рической тригонометрией. У нее была своя область приложений: помимо решения задач на определе­ние расстояний до недоступных объектов, она яв­лялась частью практической астрономии — фигуры на сфере проектировались на плоскость горизонта, меридиана и т.д., и таким образом многие задачи сводились к плоским случаям.

Отдельные вопросы из тригонометрии уже ус­пешно решали древнегреческие астрономы, одна­ко они рассматривали хорды, а не синусы, косину­сы и другие, как говорили в древности, линии. Если говорить точнее, то греческие астрономы рассмат­ривали по сути только синус, вместо которого ис­пользовали хорду, равную удвоенной линии синуса половинной дуги.

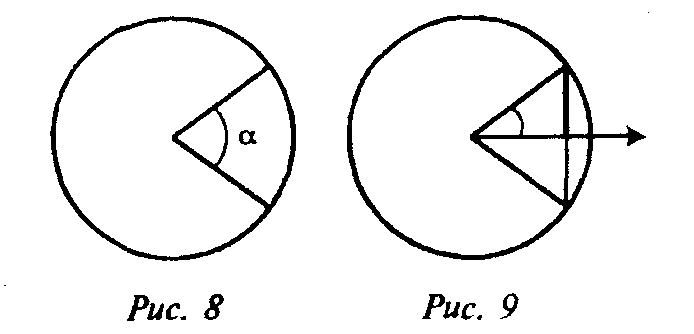
Метод составления тригонометрических таблиц состоял в следующем. В основе всех построений астрономов древности находится круг заданного диаметра. На нем рассматривалась единственная тригонометрическая характеристика: длина хорды, стягивающей дугу, соответстствующую данному центральному углу (рис. 8). Задача состояла в со­ставлении таблицы значений этой функции с наи­большей, по возможности, точностью и высокой частотой в последовательности значений аргумен­та. По существу таблицы хорд являются таблицами синусов.

Первые тригонометрические таблицы (таблицы хорд), которые положили начало вычислительной тригонометрии, составил еще во II в. до н.э. древ­негреческий астроном Гиппарх. Венцом же разви­тия астрономии и тригонометрии в Древней Греции можно считать работу «Большое математичес­кое построение астрономии в 13 книгах» («Альма­гест») знаменитого астронома Клавдия Птолемея (II в. н.э.). Сведения по прямолинейной и сфери­ческой тригонометрии изложены в первой книге «Альмагеста». Показывая, как вычислять хорды, Птолемей делил окружность на 360 частей (граду­сов). Он составил такую таблицу синусов (хорд), которая много веков была единственным пособи­ем при решении задач о треугольниках.

Начало учению о тригонометрических величинах было положено в Индии, начиная с IV-VI вв. Ин­дийские ученые впервые в науке стали употреблять линию синуса как половину хорды, и составили первые тригонометрические таблицы синусов (по­лухорд). Им были известны также основное триго­нометрическое тождество, формулы приведения, формула синуса половинного угла.

Заметим, что греческое слово хорде, от которого происходит наш термин «хорда», буквально озна­чает «тетива лука», «струна». Индийские ученые впервые предложили рассматривать величину по­лухорды (синуса), которую называли архаджива, что буквально означает «половина тетивы лука», но потом стали называть джива, что значит «тетива лука».

Как по примеру индийских математиков не уви­деть на рис. 9 лук с натянутой стрелой?

Арабские математики, которые позже (начиная с VIII в.) осваивали накопленные математичес­кие знания, писали слово джива в арабской транскрипции как джиба, что созвучно арабско­му слову джайб, которое дословно означает «па­зуха».

Вместе с военными завоеваниями арабов слово «пазуха» для обозначения полухорды в тригоно­метрии попало в Европу (X—XII вв.), где евро­пейские ученые перевели его на латынь как «си­нус». Поскольку латинский язык считался обще­признанным научным языком в Европе, то тер­мин «синус» нашел там широкое распостранение и сохранился до настоящего времени. Кста­ти, этот термин применяется не только в мате­матике: сейчас в медицине заболевание пазух носа называют синуситом. Индийские ученые рассматривали линии синуса BD и косинуса OD (рис. 10) только для острого угла.

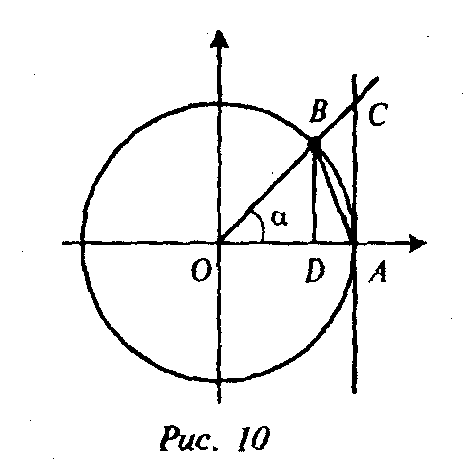
Интересно заметить, что европейские математики XII—XVI вв. часто называли синус sinus rectus (пря­мой синус), а радиус тригонометрической окружнос­ти sinus totus, т.е. весь (полный) синус. Слово «косинус» — это сокращение латинского выра­жения complementy sinus, т.е. «дополнительный синус» или, иначе, «синус дополнительной дуги»; вспомни­те: cos a = sin (90° - а).

В IX-X вв. центр математических исследований, значит, и центр развития тригонометрического зна­ния, переместился в Среднюю Азию, где трудами арабских математиков тригонометрия впервые вы­делилась из астрономии как самостоятельная на­ука. В частности, ученые стран ислама ввели новые тригонометричекие величины: тангенс и котангенс. В трактате «Плоские четырехсторонники» ученого-энциклопедиста и государственного деятеля XIII в. Насирэддина Туей плоская и сферическая тригоно­метрия выступают как самостоятельные предметы. Для сравнения, в Европе тригонометрия достигла 'этого уровня, стала успешно развиваться и тракто­ваться как самостоятельная наука лишь в XV в., и начало этому было положено трудами немецкого ас­тронома и математика, профессора Региомонтана.

Понятия «тангенс» и «котангенс», как и первые таблицы этих новых тригонометрических величин, родились не из рассмотрения тригонометрической окружности, а из учения о солнечных часах — гномоники. Солнечные часы первоначально представ­ляли собой шест, вертикально воткнутый в землю (греческое слово гномон - название этого шеста - означает «распознаватель»). Время отсчитывалось подлине и направлению тени, отбрасываемой ше­стом (рис. 1П.

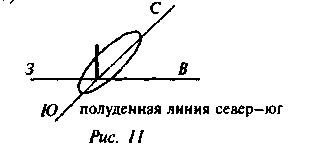
Один из современников ал-Хорезми (IX в.)' математик и астроном Ахмед ал-Мазави, названный «Вычислитель» (ал-Хабаш, ал-Хасиб), занимаясь гномоникой, констатировал, что отношение дли­ны тени и к постоянной длине / гномона солнеч­ных часов меняется в зависимости от высоты Солн­ца, измеряемой углом <р. Он принял / за 1 и со­ставил таблицу значений теней (и), соответствую­щих значениям углов 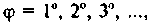т.е. (в со­временной символике) u = /ctgq>, или (если учесть, что 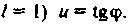Эта таблица дала возможность определять высоту Солнца по длине тени. Отно­шение длины тени к длине шеста определяет высо­ту солнца над горизонтом (рис. 12, а).

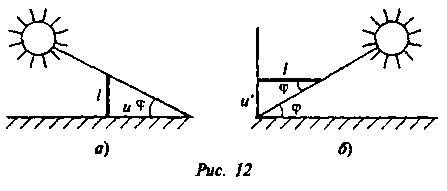
Для случая горизонтального гномона, перпенди­кулярного к вертикальной стене (рис. 12, ff), ал-Хабаш составил таблицу обращенных теней:

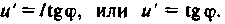
Живший в конце X в. в Багдаде Абу-ль-Вафа в сво­ей «Совершенной книге» — своем «Альмагесте»² — вводил тригонометрические линии не через пря­моугольный треугольник, а с помощью окружнос­ти, определяя, например, тангенс как отрезок ка­сательной к окружности. В некоторых местах Абу-ль-Вафа принимал радиус окружности за единицу.

Начиная с XIV—XV вв. центр математических исследований перемещается в Европу. В XIII— XIV вв. при переводе арабских произведений на ла­тинский язык новые тригонометрические функции котангенс и тангенс были названы umbra recta -прямая тень, и umbra versa — обратная тень. Изве­стно, что линию тангенсов уже использовал в сво­их работах английский математик Томас Брадвар-дин (1290-1349).

Термин tangens (от лат. касающийся [отрезок ка­сательной]) был введен только в 1583 г. датским математиком Томасом Финком в связи с ролью этой линии на тригонометрической окружности. Термин «котангенс» образован по аналогии с тер­мином «косинус», и встречается впервые в 1620 г. у английского ученого Эдмунта Гутера.

В Европе первое сочинение, в котором тригономе­трия рассматривалась как самостоятельная математическая дисциплина, написал в 1462—1464 гг. немец­кий математик и астроном Региомонтан. Он называл свой труд «Пять книг о треугольниках всех видов». В это время тригонометрия no-прежнему продолжала формироваться и развиваться под определяющим влиянием астрономии. В XV—XVI вв. усовершенствовались таблицы тригонометрических функций, которые были необходимы астрономам, разрабаты­вались все новые вычислительные приемы³, рассма­тривались все более сложные задачи решения плос­ких и сферических треугольников, оттачивалась тех­ника работы с тригонометрическими линиями.

В XVI в. французский математик Франсуа Виет (1540—1603) использовал тригонометрию для ре­шения кубического уравнения. В некоторых его результатах устанавливалась связь между тригоно­метрией и алгеброй. Кроме того, он положил на­чало буквенным обозначениям в тригонометрии. Таким образом, на пороге XVII в. в развитии тригонометрии наметилось новое направление — ана­литическое. Если до этого главной целью триго­нометрии считалось решение треугольников, вы­числение элементов геометрических фигур, а уче­ние о тригонометрических функциях строилось на геометрической основе, то развитие нового (ана­литического) направления привело к тому, что тригонометрия постепенно стала одной из глав математического анализа. Начало этого преобра­жения тригонометрии связано с именем знамени­того ученого много лет работавшего в Петербурге Леонарда Эйлера (1707—1783). Эйлер усовершен­ствовал как символику, так и содержание триго­нометрии. Перечислим некоторые его нововведе­ния в этой области.

1. До Эйлера совсем редко рассматривались три­гонометрические функции дуг, превышающих л. Лишь в его трудах разрабатывается учение о триго­нометрических функциях любого аргумента и впер­вые ясно изложен вопрос о знаках тригонометри­ческих функций в каждом квадранте.

2. В отличие от своих предшественников Эйлер исключил из своих формул R - целый синус (sinus totus), принимая R = 1 и упрощая, таким образом, записи и вычисления.

3. Понимая аргумент тригонометрической функ­ции не только как угол или дугу, а как любую чис­ловую величину, Эйлер впервые стал систематиче­ски излагать тригонометрию аналитическим путем. До него каждая тригонометрическая теорема дока­зывалась отдельно на основании соответствующе­го каждому случаю геометрического чертежа. Эй­лер же выводил теоремы, исходя из небольшого числа основных соотношений.

4. Для обозначения тригонометрических функ­ций Эйлер использовал символы sinx, cosx, tangx, cotjf и т.д., а также ввел употребляемые поныне обозначения а, Ь, с для сторон и А, В, С для соответствующих противоположных углов треуголь­ника ABC, что способствовало появлению единой символики в тригонометрии.

5. Эйлер стал рассматривать тригонометрию как науку о тригонометрических функциях и придал ей современный вид.

Таким образом, именно имя Эйлера должен по­мнить учащийся, который учится работать с триго­нометрической окружностью, выводит формулы тригонометрии, учится решать тригонометрические уравнения и неравенства, изучает свойства триго­нометрических функций.

В наше время тригонометрия больше не рассма­тривается как самостоятельная ветвь математики. Важнейшая ее часть — учение о тригонометричес­ких функциях — является частью более общего, по­строенного с единой точки зрения учения о функ­циях, изучаемых в математическом анализе. Другая же часть — решение треугольников — рассматрива­ется как глава геометрии.

Третья часть-это широкое применение в других областях, например, в физике.

6. Практическая работа.

Н

айдите коэффициент трения между вашей ручкой и бумагой

7. Итог урока. Задание на дом:

Это хорошо решить!

1. Решите уравнение:

а) (2х-3)│sin x│=sin x;

б)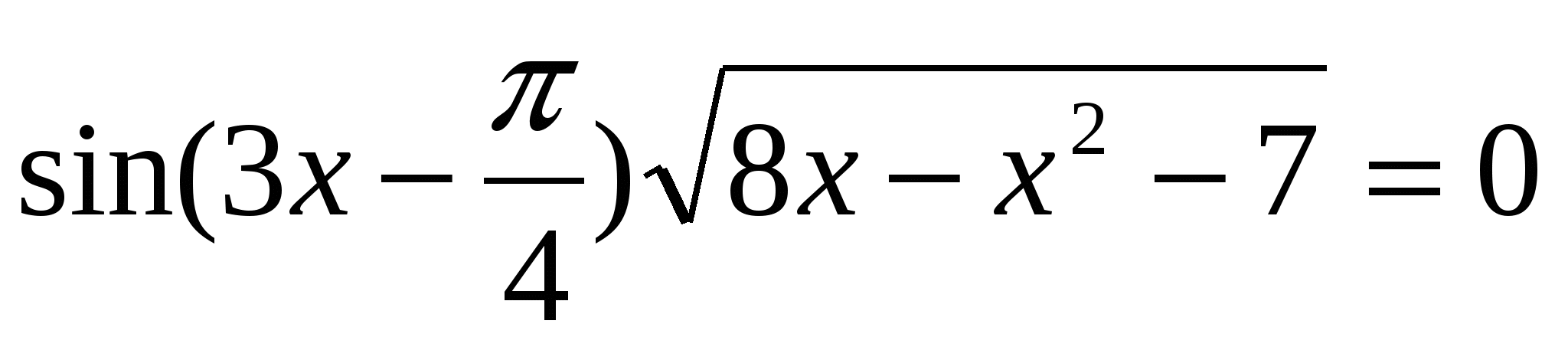

2. Как влияет разбег на дальность полета мяча брошенного под углом к горизонту?

Домашнее задание.

Как влияет разбег на дальность полета мяча, брошенного под углом к горизонту? Пусть Δl –увеличение дальности полета за счет разбега. Полагая, что за счет разбега мячу сообщается дополнительная горизонтальная скорость, а вертикальная составляющая практически не меняется, получаем 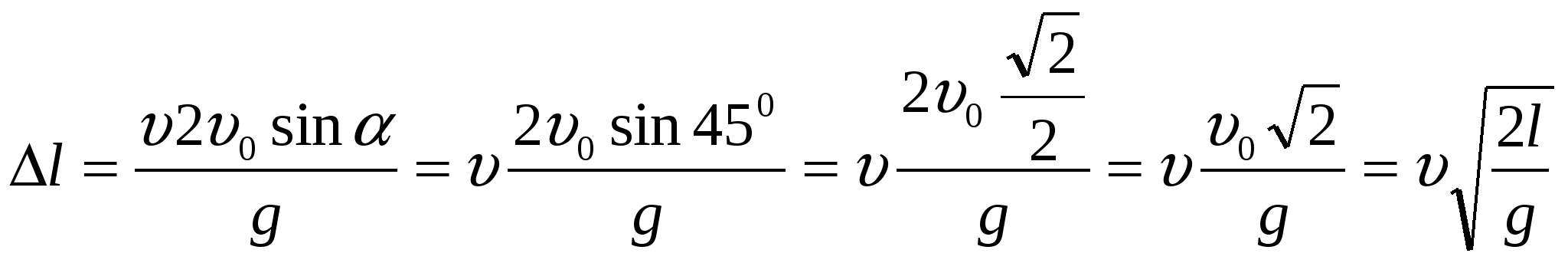где υ₀ – начальная скорость броска, l дальность полета без разбега вся дальность полета будет l+Δl.

Используемая литература:

1. Власова И.Н., Малых А. Е. Очерки по истории эле­ментарной геометрии. (Материалы для спецкурса по геометрии.) - Пермь, 1998.

2. Глейзер Г.И. История математики в школе: VII-VUI кл. - М: Просвещение, 1982.

3. Глейзер Г.И. История математики в школе: IX— X кл. - М.: Просвещение, 1983.

4. Рыбников К.А. История математики: Учебник. - М.: Изд-во МГУ, 1994.

5. Чистяков В.Д. Материалы по истории математики в Китае и Индии. - М.: Учпедгиз, 1960.

6. Мордкович А.Г., П.В. Семенов Алгебра и начала анализа 10 класс (профильный уровень)М: Мнемозина 2005

7. Б.И. Вершинин, С.Н. Постников. Сборник задач по физике .Томск. Пеленг,1997

8. В.А. Касьянов . Физика 10 (профильный уровень)

Список использованной литературы

1. Иванов Б.А., Петров В.И. Литература. 10-11 класс. Ч.2.- М.: ООО «Обучение», 2006

2. Григорьев М.И. Анализ стихотворного текста – М.: «Ученик», 2003.

Использованные материалы и Интернет-ресурсы

1. Видеокассета «Культура России. Серебряный век», 2006 г.2. Иванов И.С. «Великая Россия», CD, 2007 г.3. Петров Т.И., песня «Россия» 4. http://sitename.ru