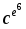
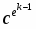
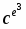
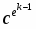
Реферат на тему:
RSA – алгоритмів кодування з відкритим ключем
Перший алгоритм кодування з відкритим ключем (Public Key Encryption, далі PKE) було запропоновано Вітфілдом Діффі та Мартіном Хелманом у Стендфордському університеті. Вони, а також незалежно від них Ральф Меркл, розробили основні його поняття у 1976 році. Перевага PKE полягає у відсутності потреби секретної передачи ключа.
PKE базується на нерозв’язності проблеми розкладу натурального числа на прості множники.
RSA схему шифрування було запропоновано у 1978 році та названо іменами трьох його винахідників: Роном Рівестом (Ron Rivest), Аді Шаміром (Adi Shamir) та Леонардом Адлеманом (Leonard Adleman). RSA належить до класу алгоритмів кодування з відкритим ключем.
У 80-х роках криптосистема переважно використовувалася для забезпечення секретності та достовірності цифрових даних. У сучасному світі RSA використовується в web – серверах та браузерах для зберігання таємності даних що передаються по мережі, .
Схема RSA базується на обчисленні виразів зі степенями. Відкритий текст шифрується блоками, довжина кожного із яких менша за деяке число n.
Алгоритм генерації ключа
A повинен згенерувати відкритий та секретний ключі:
1. Згенерувати два великих простих числа p та q приблизно однакової довжини;
2. Обчислити n = p * q, fi = (p – 1) * (q – 1);
3. Вибрати натуральне e, 1 < e < fi, взаємно просте з fi;
4. Використовуючи розширений алгоритм Евкліда, розв’язати рівняння
d * e 1 (mod fi).
Відкритий ключ: (n, e). Секретний ключ: d.
Схема шифрування RSA
B шифрує повідомлення m та надсилає A.
1. Шифрування. В робить наступні дії:
а) отримати відкритий ключ (n, e) від А;
б) представити повідомлення у вигляді натурального числа m з проміжку [1..n];
в) обчислити c = me mod n;
г) надіслати шифротекст c до А.
2. Дешифрування. Для отримання повідомлення m із шифротксту c А робить наступні дії:
а) використовуючи секретний ключ d, обчислити m = cd mod n.
Теорема. Шифр c декодується правильно.
Оскільки p та q – прості числа, то (p * q) = (n) = (p - 1) * (q - 1), де – функція Ейлера. З умови вибору ключа d маємо: d * e mod (n) = 1, або d * e = (n) * k + 1 для деякого натурального k.
cd mod n = (me)d mod n = m (e * d) mod n = m ^ ( (n) * k + 1) mod n = (m (n) mod n) k * m = 1 k * m = m, оскільки за теоремою Ейлера m (n) mod n = 1.
Означення. RSA системою називають функцію RSAn,e(x) = xe mod n та обернену їй RSA-1n,e(y) = yd mod n, де e – кодуюча, а d – декодуюча експонента, x, y Zn*.
Приклад
1. Оберемо два простих числа: p = 17, q = 19;
2. Обчислимо n = 17 * 19 = 323, fi = (p - 1) * (q - 1) = 16 * 18 = 288;
3. Оберемо e = 7 (НСД(e, fi) = 1) та розв’яжемо рівняння 7 * d 1 (mod 288), звідки d = 247.
Побудовано RSA систему: p = 17, q = 19, n = 323, e = 7, d = 247.
Відкритий ключ: n = 323, e = 7, секретний ключ: d = 247.
1. m = 4. Кодування: 47 mod 323 = 234. Декодування: 234247 mod 323 = 4.
2. m = 123. Кодування: 1237 mod 323 = 251. Декодування: 251247 mod 323 = 123.
Циклічна атака
За відомим шифром c (c = me mod n) злодій, маючи відкритий ключ e та n, бажає знайти повідомлення m. Він починає будувати послідовність чисел
c, ce,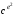 
, , …
Оскільки обчислення відбуваються в групі Zn*, то елемпнти послідовності знаходяться в межах від 0 до n - 1. Отже існує таке натуральне k, що с =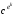 
. Враховуючи що c = me mod n, маємо: me = 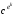або m = .
Таким чином для знаходження повідомлення m за його шифром c необхідно побудувати послідовність c, ce, 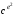, , …, , 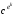= c, і взяти її передостаннє число.
Приклад
Розв’язати рівняння: m7 mod 323 = 251.
e = 7, n = 323, c = 251.
-
k
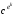
0
251
1
310
2
47
3
4
4
234
5
123
6
251
З таблиці маємо: c = = 251. Оскільки me =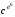 
, то m = 
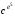= 123.
Атака методом осліплення
Припустимо, А має секретний ключ RSA системи, а Z – злодій, який перехопив шифр c і хоче декодувати його. При цьому А відмовляє видати Z вихідний текст m. Тоді Z обирає деяке значення b Zn*, обчислює c’ = be * c і просить А дешифрувати його. А погоджується дешифрувати c’ своїм секретним ключем d, оскільки зміст повідомлення c’ йому ні про що не говорить і виглядає невинним. Отримавши m’ = c’d mod n, злодій Z обчислює m = m’ / b і отримує шукане m. Шифром m дійсно є c, оскільки me = m’e / be = c’de / be = c’ / be = c.
Така атака можлива, оскільки А не знає повної інформації про шифр c’, який дає йому злодій Z.
Приклад. Нехай А має RSA систему: p =17, q = 19, n = 323, e = 7, d = 247.
Злодій Z перехопив шифр c = 234 і хоче знайти таке m, що m7 = 234 mod 323.
1. Z обирає b = 10 Z323*, обчислює c’ = 107 * 234 mod 323 = 14 і просить А дешифрувати його.
A обчислює m’ = 14247 mod 323 = 40 і передає його Z.
3. Z знаходить шукане повідомлення обчислюючи
m = 40 / 10 = 40 * 10-1 = 40 * 97 = 4 mod 323.
Таким чином 47 = 234 mod 323.
Прискорення дешифрування
За допомогою китайської теореми про лишки можна прискорити процес дешифрування, знаючи секретні прості числа p та q.
Алгоритм
Дешифрування. А має декодуючу експоненту d, а також p та q (n = p * q). А отримує від В шифр с та повинен виконати операцію cd (mod n).
1. Обчислити dp = d mod (p - 1), dq = d mod (q - 1)
2. Обчислити mp =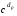 
mod p, mq = 
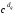mod q.
3. Розв’язати систему лінійних порівнянь
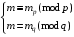
Розв’язком системи буде декодоване повідомлення: m = cd (mod n).
Приклад
Нехай RSA система має вигляд: p = 17, q = 19, n = 323, e = 7, d = 247.
Для розв’язку рівняння m7 mod 323 = 251 (c = 251) обчислимо 251247 mod 323:
1. dp = 247 mod 16 = 7, dq = 247 mod 18 = 13;
2., mp = 2517 mod 17 = 4, mq = 25113 mod 19 = 9;
3. Розв’яжемо систему лінійних порівнянь
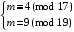
Розв’язуючи її методом Гауса, отримаємо m = 123.
Отже 1237 mod 323 = 251.
Мала декодуюча експонента
Приклад. Виберемо аовідомлення m = 13 та зашифруємо його трьома різними RSA системами.
1. p = 5, q = 17, n = 85, e = 3, d = 57,
m3 mod 85 = 72;
2. p = 11, q = 23, n = 253, e = 3, d = 169,
m3 mod 253 = 173;
3. p = 17, q = 23, n = 391, e = 3, d = 261,
m3 mod 391 = 242;
Для знаходження повідомлення m за відкритими ключами (ni, ei ) та перехопленими шифрами ci складемо систему порівнянь
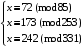
Одним із її розв’язків буде x = 2197 = 133. Тобто шуканим повідомленням буде m = 13.
Неприховані повідомлення
Означення. Повідомлення m називається неприхованим, якщо його шифр дорівнює самому повідомленню, тобто me = m (mod n).
Наприклад, повідомлення m = 0 та m = 1 завжди є неприхованими для довільних значень e та m.
Твердження. Кількість неприхованих повідомлень в RSA системі дорівнює
(1 + НСД(e - 1, p - 1)) * (1 + НСД(e - 1, q - 1))
Оскільки значення e - 1, p - 1 та q - 1 – парні, то НСД(e - 1, p - 1) 2, НСД(e - 1, q - 1) 2, а отже кількість неприхованих повідомлень завжди не менша за 9.