Ряди динаміки 2

Ряди динаміки

План

1. Статистичні ряди динаміки та їх види.

2. Показники для характеристики ряду динаміки.

3. Основні прийоми аналізу та перетворення рядів динаміки.

1. Суспільні явища безперервно змінюються, розвиваючись у просторі і часі. Протягом певного часу – місяць за місяцем, рік за роком – змінюються чисельність населення, обсяг випущеної продукції, структура суспільного виробництва.

Поступальний розвиток, зміна явищ у часі називаються динамікою. Вивчення динаміки змін суспільно-економічних явищ – одне з найголовніших завдань статистики.

Для зручності систематизують дані про розвиток явищ у часі систематизують у вигляді рядів динаміки.

Ряд динаміки – це ряд розміщених у хронологічній послідовності статистичних показників.

Ряд динаміки складається з двох елементів: рівнів ряду – статистичних показників; моментів (періодів) часу, до яких належать ці рівні.

Показники завжди записуються під періодами часу.

Приклад 1. Дано показники новонароджених у 1999 р.

Приклад 2. Дано залишки вкладів населення в Ощадбанку у 1998 р.

Розрізняють два види рядів динаміки: інтервальні – рівні ряду характеризують явище за певні періоди часу; моментні – показники ряду характеризують явище на певний момент часу.

Прикладом інтервального ряду є приклад 1, моментного ряду – приклад 2.

Рівні динамічного ряду можуть бути абсолютними, відносними та середніми величинами. В обох наведених прикладах статистичні показники є абсолютними величинами. Періоди часу інтервального ряду динаміки можна збільшувати або розкладати на частини, якщо рівні ряду – абсолютні величини. Так, у прикладі 1 можна зменшити кількість періодів і обчислити кількість новонароджених у І та ІІ півріччі.

Підсумовування рядів інтервального ряду абсолютних величин є важливою властивістю цього виду рядів динаміки. Водночас сума показників моментного ряду не має реального змісту, оскільки це призводить до повторного рахунку.

Не можна додавати рівні рядів динаміки відносних та середніх величин, оскільки вони є величинами похідними і отримана сума не матиме економічного змісту.

2. Для рядів динаміки економічних показників характерним є відображення динамічності економіки. Збільшення виробничих ресурсів, підвищення технічного рівня, продуктивності праці, поліпшення соціальних умов виробництва ведуть за собою нарощення виробництва, економічне зростання. Водночас ряд інших об’єктивних і суб'єктивних факторів (інфляція, затримки планшетів і т.п.) гальмують це зростання, призводить до зниження виробництва й економічного спаду.

На основі рівнів ряду динаміки визначають систему показників, які дають всебічну характеристику напряму та інтенсивності змін явища у часі.

Ця система включає такі показники:

абсолютний приріст;

темп зростання;

темп приросту;

абсолютне значення 1% приросту.

Абсолютний приріст – це різниця між наступним і попереднім, або базисним, рівнями ряду. Він показує, на скільки одиниць наступний рівень відрізняється від попереднього, що прийнятий за базу порівняння (швидкість зміни).

Абсолютний приріст може бути додатнім (динаміка зростання), від’ємним (зменшенням) або нульовим (без змін).

Абсолютний приріст призначається буквою ∆, вимірюється в одиницях виміру ознаки та обчислюється за формулами:

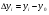- базисні абсолютні прирости;

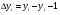- ланцюгові абсолютні прирости.

Базисні та ланцюгові прирости адитивно пов'язані: сума ланцюгових приростів дорівнює загальному базисному приросту за весь період:

.

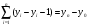Коефіцієнт зростання – це відношення наступних показників до попередніх, з якими їх порівнюють. Він збігається з поняттям, вивченим раніше, - відносною величиною динаміки і показує інтенсивність зміни рівнів ряду.

Коефіцієнти зростання позначають буквою К і вимірюють у коефіцієнтах або у відсотках множенням коефіцієнта на 100%.

Якщо коефіцієнт зростання певного рівня більший за одиницю (К>1), то це свідчить про зростання рівня, якщо К< 1 – про зниження.

Коефіцієнти зростання обчислюються за формулами:

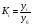- базисні коефіцієнти зростання,

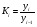- ланцюгові коефіцієнти зростання.

Між ланцюговими і базисними коефіцієнтами зростання існує мультиплікативний зв'язок.

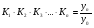, де К₁, К₂, К₃,…, К_п – ланцюгові коефіцієнти зростання.

Отже, базисний коефіцієнт зростання 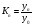можна обчислити як добуток п ланцюгових коефіцієнтів зростання.

Темп приросту – це відношення абсолютного приросту до попереднього рівня ряду (або базисною), виражене у відсотках. Він є вимірником відносної швидкості зростання і показує, на скільки відсотків збільшився (зменшився) показник (наступний рівень) порівняно з попереднім чи базисним.

Додатне значення темпу приросту свідчить про зростання рівня, а від’ємне – про зниження (темпи падіння). Позначається він буквою Т (темп).

Згідно із визначенням, темпи приросту обчислюються за формулами:

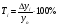- базисні темпи приросту;

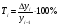- ланцюгові темпи приросту.

Але у практиці використовують більш зручну формулу

.

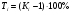Отже, темп приросту визначаємо як різницю темпу зростання “мінус” “1”, а результат множимо на 100%. А якщо коефіцієнт зростання обчислений у відсотках, то від нього віднімають 100%.

Слід пам’ятати, що ланцюгові темпи приросту можна отримати лише віднімаючи 1 (чи 100%) від ланцюгових темпів зростання. Аналогічно визначаємо базисні темпи.

Абсолютне значення 1% приросту – це відношення абсолютного приросту за певний час до темпу приросту цього самого періоду. Цей показник розкриває вагомість 1% приросту, його вираження в абсолютній величині. Він показує, що означає підвищити або знищити рівень певного суспільного явища на один відсоток. Абсолютне значення 1% приросту вимірюється в одиницях рівнів ряду, позначається |1%| і обчислюється за формулою:

.

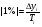Показник абсолютного значення одного відсотка приросту (|1%|) модна також одержати, якщо поділити абсолютний рівень попереднього періоду на 100:

.

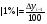Обчислені показники аналізу рядів динаміки зручно подавати у вигляді таблиць. Це допомагає виявити тенденції у динаміці явища, порівняти окремі показники.

Для узагальнення оцінок швидкості та інтенсивності зростання використовують середні значення показників аналізу.

Середній абсолютний приріст обчислюють за формулою середньої арифметичної простої з ланцюгових приростів

,

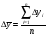де п – кількість ланцюгових абсолютних приростів.

Якщо відомі базисні прирости, то зручніше обчислювати 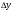за формулою

.

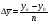Середній темп зростання (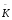)обчислюють за формулою середньої геометричної:

,

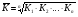де К₁, К₂,…, К_п – ланцюгові темпи зростання, п – кількість ланцюгових темпів зростання.

Середній темп приросту обчислюють як різницю між середнім темпом зростання (у %) і 100 % за формулою

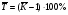
Середнє значення 1% приросту обчислюються як відношення середнього абсолютного приросту до середнього темпу приросту

.

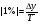3. При вивченні динаміки соціально-економічного розвитку статистика вивчає інтенсивність розвитку за допомогою показників, які ми розглянули, виявляє тенденції розвитку, оцінює структурні зрушення, виявляє фактори економічного зростання.

Тенденція – повний напрямок розвитку, тривала еволюція (тенденція до росту, стабільності або до зниження рівнів явища).

Щоб виявити тенденція ряду динаміки, статистика використовує певні прийоми обробки рядів динаміки.

Найпростіший прийом - збільшення періодів часу, до яких відносяться рівні динамічного ряду. Замість щоденних рівнів обчислюються декади (10 днів), щомісячні, квартальні, замість щорічних обчислюються п’ятирічні рівні.

Другий прийом обробки – метод плинної середньої. Суть методу у тому, що обчислюється середній рівень спочатку з повного числа перших за лічбою рівнів ряду, потім з того ж числа рівнів, але починаючи з другого за лічбою, далі починаючи з третього і т.д.

Більш складними прийомами виявлення тенденції розвитку є “трендові криві”, тобто на основі фактичних даних ряду динаміки підбирається математична функція, за допомогою якої описується основна тенденція f(А). рівні ряду динаміки розглядаються як функція часу, і завдання зводиться до визначення виду функції, обчислення її параметрів за емпіричними даними та розрахунку теоретичних рівнів за формулою.

Третій прийом – екстраполяція та інтерполяція. Якщо треба обчислити декілька відсутніх, невідомих проміжних рівнів ряду динаміки, застосовують прийом інтерполяції. Інтерполяція – приблизний розрахунок, що базується на закономірності розвитку явища за період, що аналізується. Точність обчислення залежить від того, що аналізується. Точність обчислення залежить від того, наскільки ця закономірність стійка, а також від стабільності показників динаміки.

Обчислення проводять на основі середнього абсолютного приросту або середнього темпу росту.

Екстраполяція – обчислення рівня ряду динаміки в майбутньому. При екстраполяції виходять з припущення, що характер динаміки, що мала місце протягом певного періоду, збережеться і в майбутньому. Екстраполяція на короткий період можлива на основі середнього абсолютного приросту, середнього темпу росту та приросту.

Екстраполяція на довгий період повинна будуватися на більш складних прийомах математичної статистики, оскільки тенденції, що мали місце в минулому, в майбутньому можуть змінитися.

Основні поняття

Руд динаміки

Абсолютний приріст

Абсолютне значення 1% приросту

Екстраполяція

Інтерполяція

Темп росту

Темп приросту

Контрольні запитання.

1. Що таке ряд динаміки?

2. З яких елементів складається динамічний ряд?

3. Назвіть види рядів динаміки.

4. Яку властивість мають рівні інтервального ряду абсолютних величин?

5. Чи можна підсумовувати рівні моментного ряду динаміки?

6. Назвіть основні показники аналізу рядів динаміки.

7. Що таке абсолютний приріст?

8. Як обчислити абсолютний приріст?

9. Що таке коефіцієнт зростання і як його обчислити?

10. Що таке темп приросту?

11. Яка практична формула для обчислення темпу приросту?

12. Що таке абсолютне значення 1% приросту і як його обчислити?

13. Як вирахувати середній абсолютний приріст?

14. Як знаходять середній коефіцієнт зростання та темп приросту?

15. Як знаходять середнє значення 1% приросту?

16. Які основні прийоми аналізу рядів динаміки?