Спецификация
итоговой работы (теста) учащихся 8 класса
общеобразовательных учреждений
по алгебре.
1. Назначение работы
Данный тест предназначен для учащихся 8 класса (УМК авторы А.Г.Мордкович и др.).
На проведение работы отводится 120 мин.
Цель работы: оценить уровень общеобразовательной подготовки по алгебре учащихся VIII классов общеобразовательных учреждений.
2. Документы, определяющие содержание работы
Содержание работы определяется на основе следующих документов:
Федеральный компонент государственного стандарта общего образования. Математика. Основное общее образование (Приказ Минобразования России от 05.03.2004 №1089 «Об утверждении федерального компонента государственных образовательных стандартов общего, основного общего и среднего (полного) общего образования»).
3. Характеристика структуры и содержания работы.
Работа состоит из двух частей.
Часть 1 направлена на проверку овладения содержанием курса на уровне базовой подготовки. Эта часть содержит 9 заданий, предусматривающих три формы ответа: задания с выбором ответа из четырех предложенных вариантов (4 задания), с кратким ответом (4 задания), задания на соотнесение (1 задание).
При выполнении заданий первой части учащиеся должны продемонстрировать определенную системность знаний и широту представлений по курсу алгебры 8 класса.
Часть 2 направлена на проверку владения материалом на повышенных уровнях. Основное ее назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленную часть учеников, составляющих потенциал предпрофильных классов.
Эта часть содержит 4 задания (с 10 по 13) разного уровня сложности, требующих развернутого ответа (с записью решения). Задания во второй части расположены по нарастанию сложности.
4.Критерии оценивания результатов выполнения работы.
Для оценивания результатов выполнения работ учащимися применяются два количественных показателя: традиционные отметки «2», «3», «4» или «5» и общий балл за верно выполненные задания первой и второй частей.
Общий балл формируется путем подсчета общего количества баллов, полученных учащимися за выполнение первой и второй частей работы. В итоге за первую часть можно получить 9 баллов, за вторую – 12 баллов, в целом за работу – 21 балл.
Система формирования общего балла
Задания
Часть 1
(задания с выбором ответа и кратким ответом)
Часть 2
(задания с развернутым ответом)
За всю работу
Задания 1-9
10
11
12
13
Максимальное число баллов
1 балл
2
3
3
4
21
Правильное выполнение каждого задания 1 части работы оценивается 1 баллом, если ответ неверный или отсутствует – 0 баллов.
Учащийся, демонстрирующий умение решить ту или иную задачу второй части работы, получает установленный балл, или балл, на 1 меньше установленного (в случае, если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения); поэлементарное оценивание не предусматривается.
Схема перевода рейтинга в отметку.
Общий балл
Выполнено менее 5 заданий
При выполнении минимального критерия
5 - 9
10 - 15
16 - 21
Отметка
«2»
«3»
«4»
«5»
5. Время выполнения работы
На проведение итоговой работы (теста) отводится 120 минут.
Текст итоговой работы (теста)
Вариант I
I часть
1. Найдите значение выражения 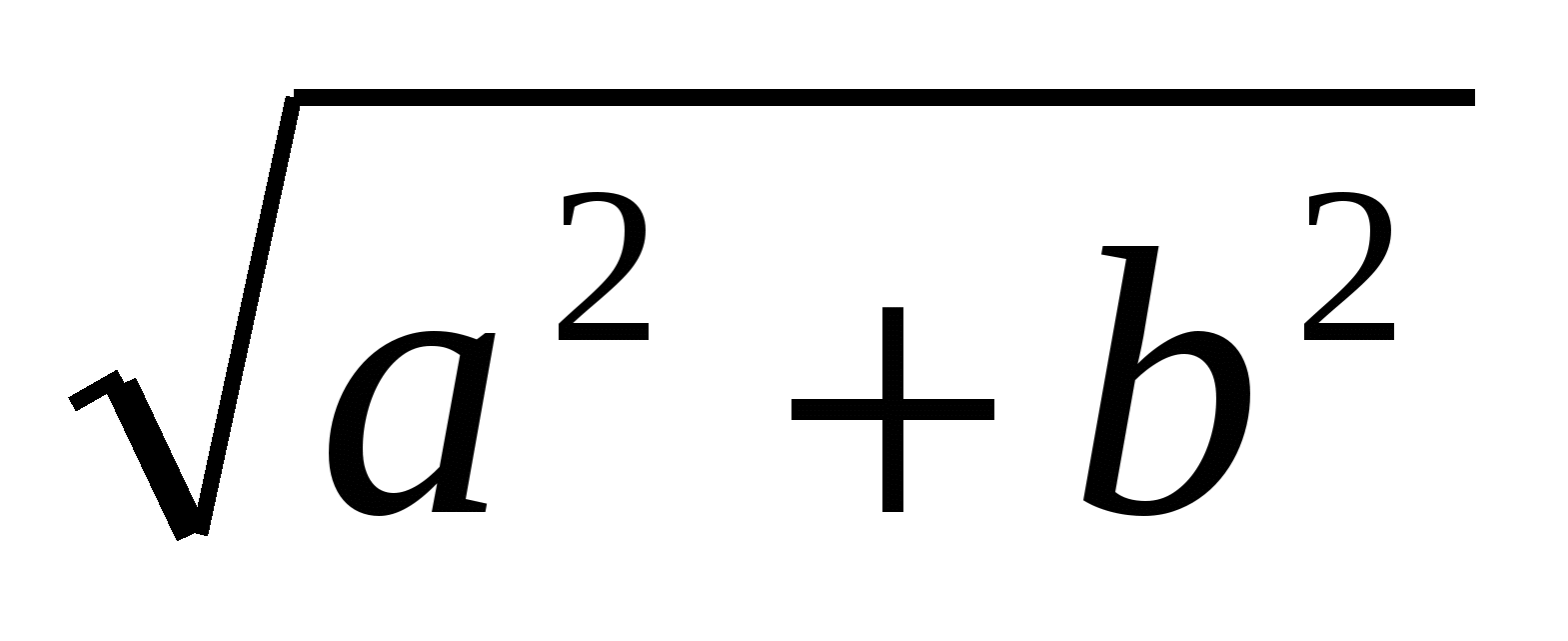 при а=12 и b= -5.
при а=12 и b= -5.
Ответ ________________
2. Упростите выражение 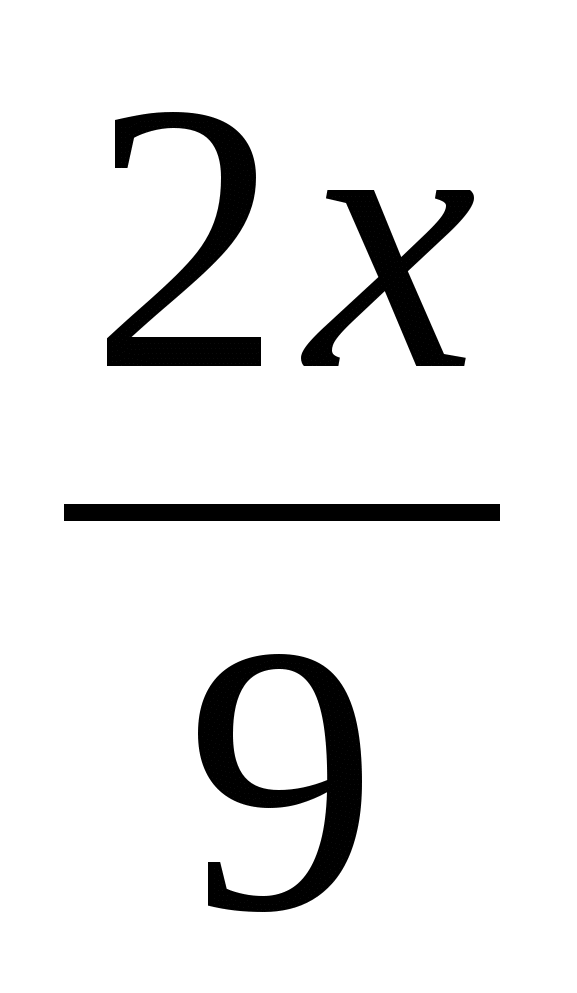 +
+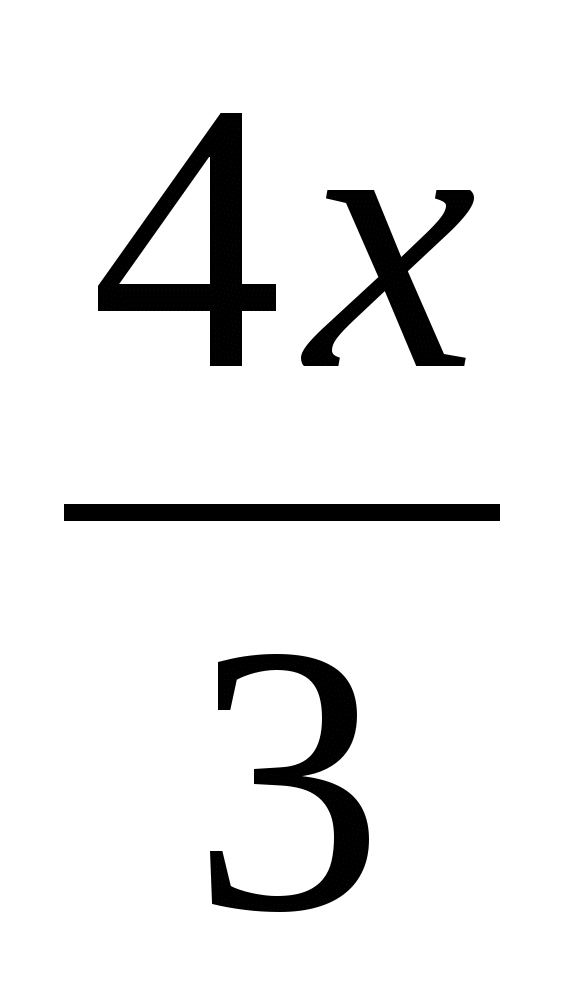 .
.
1) 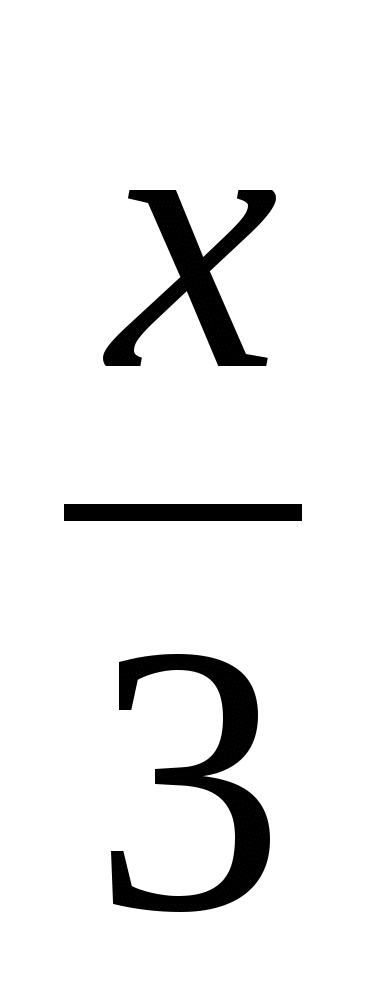 ; 2)
; 2) 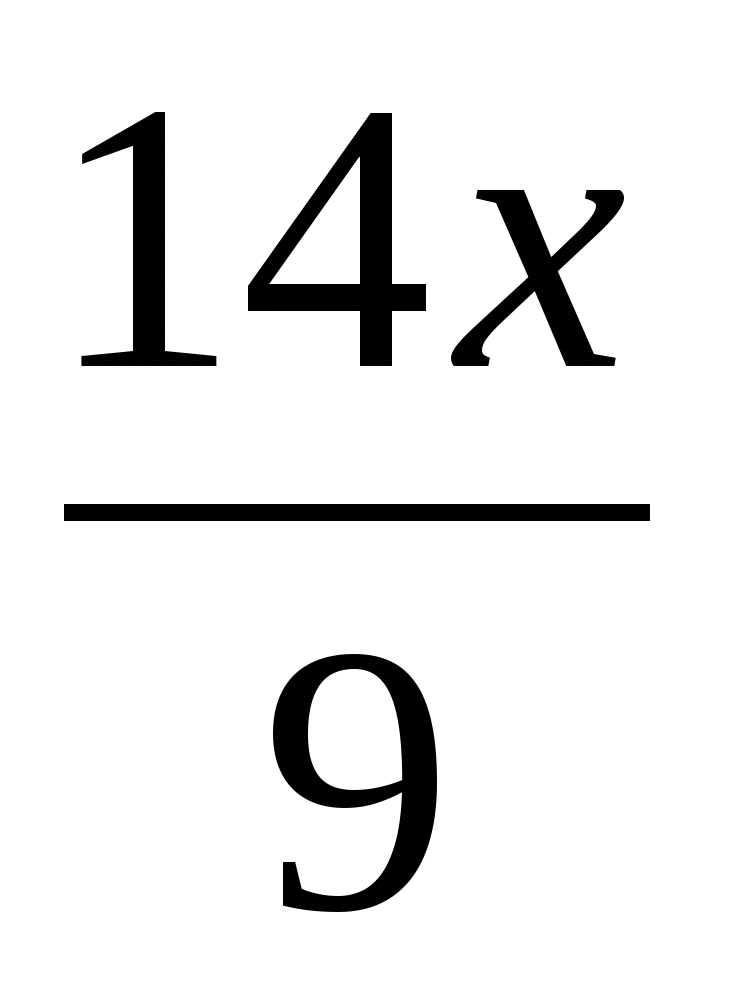 ; 3)
; 3) 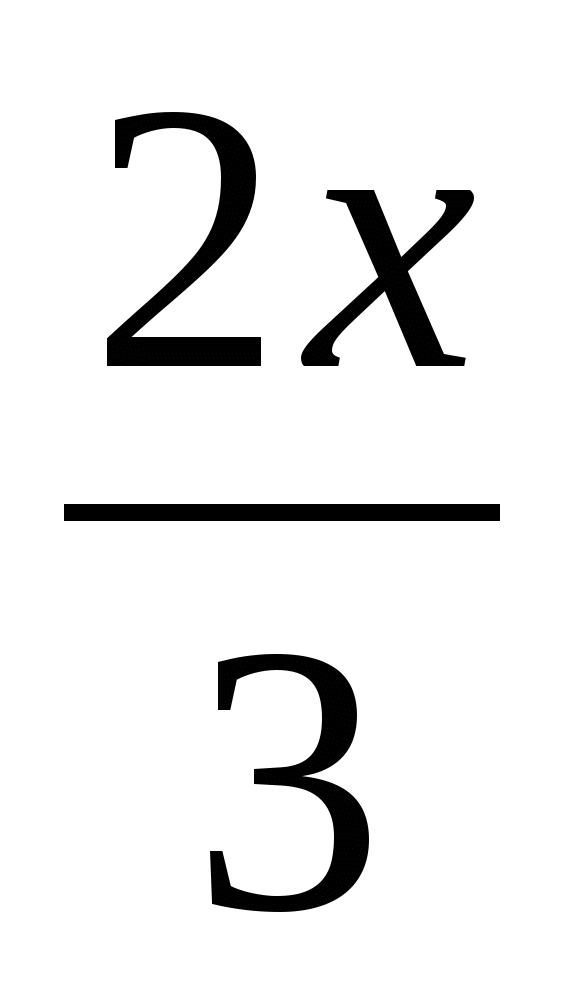 ; 4)
; 4) 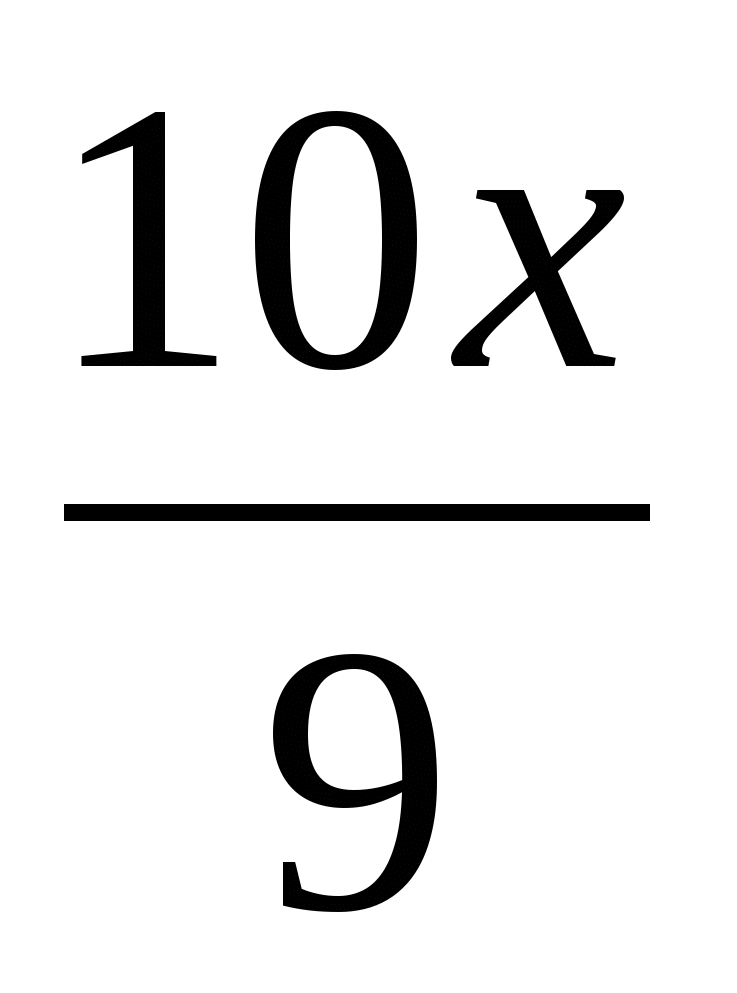 .
.
3. Решите уравнение: 2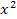 +3х-2=0.
+3х-2=0.
Ответ _______________
4. Для каждого выражения из верхней строки укажите равное ему выражение из нижней.
1) (а2)3а2; 2) (а2а3)2; 3) 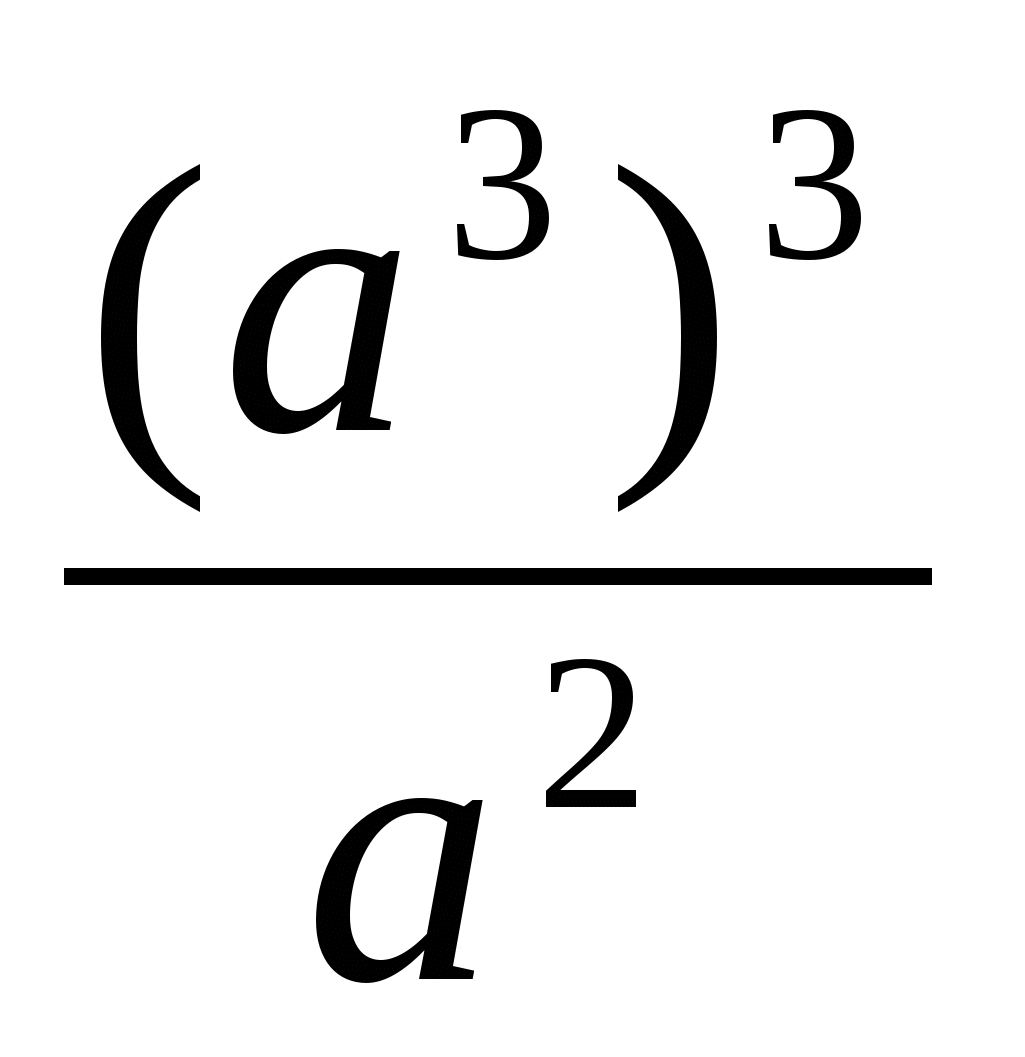 .
.
а) а7; б) а8; в) а10; г) а12.
1
2
3
5. Функции заданы формулами: а) у=х2+1; б) у=х2-1; в) у=-х2+1; г) у=-х2-1.
Графики каких из этих функций не пересекают ось х?
1) а и г; 2) б и г; 3) а и в; 4) б и в.
6. Упростите выражение 4b(b+2)-(4+b)2.
Ответ _______________
7. Составьте квадратное уравнение, корнями которого являются числа
х1=4; х2=2:
1) х2+6х-8=0; 2) х2-6х+8=0;
3) х2+6х+8=0; 4) х2-6х-8=0..
8. От города до поселка автомобиль проехал за 3 часа. Если бы он увеличил скорость на 25 км/ч, то затратил бы на этот путь на 1 ч меньше. Чему равно расстояние от города до поселка?
Пусть х км/ч – расстояние от города до поселка. Какое уравнение соответствует условию задачи?
1) 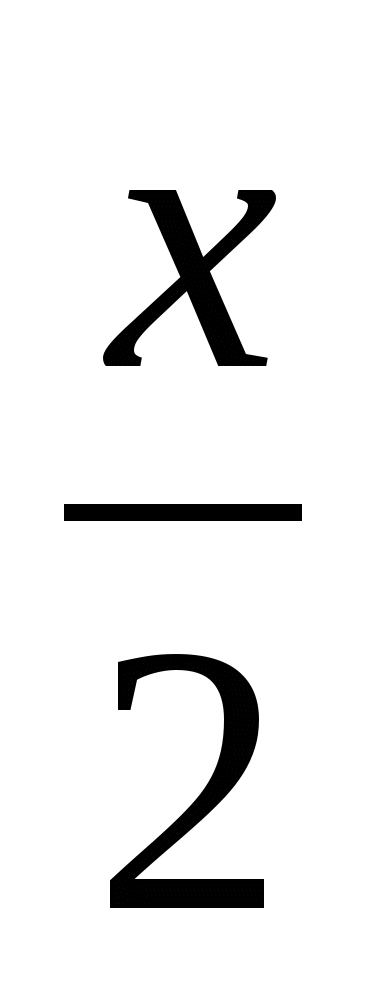 -
-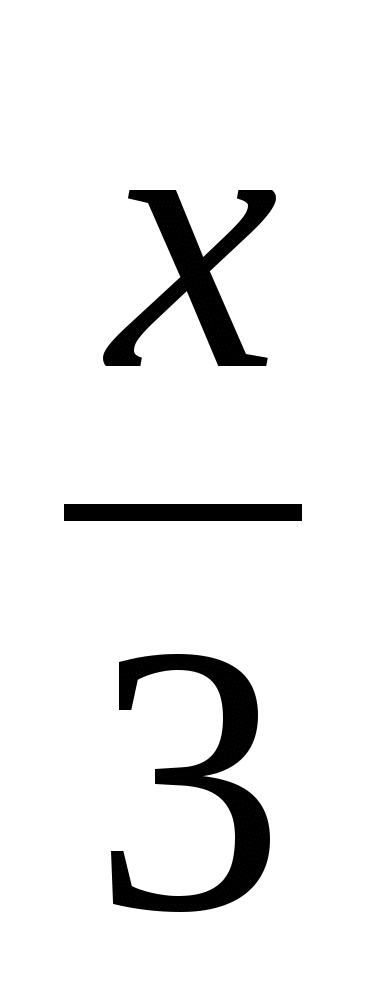 =25; 2)
=25; 2) 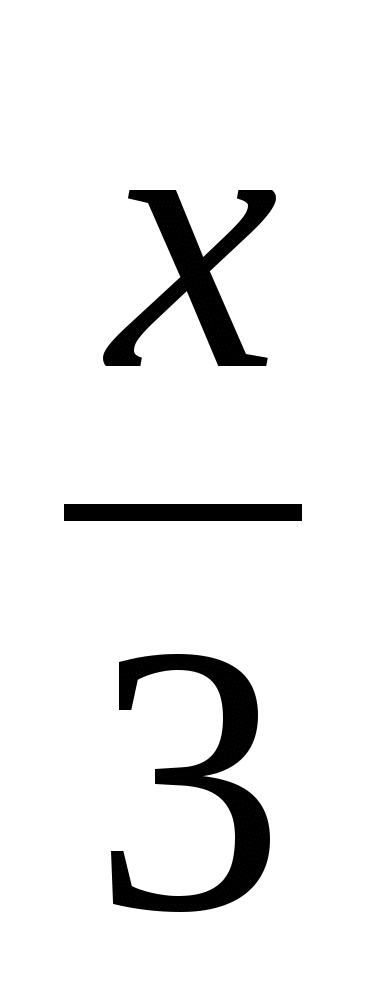 -
-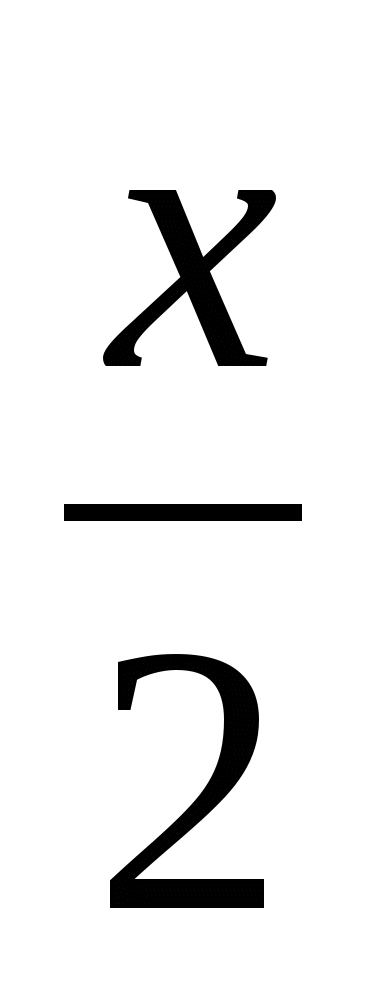 =25; 3)
=25; 3) 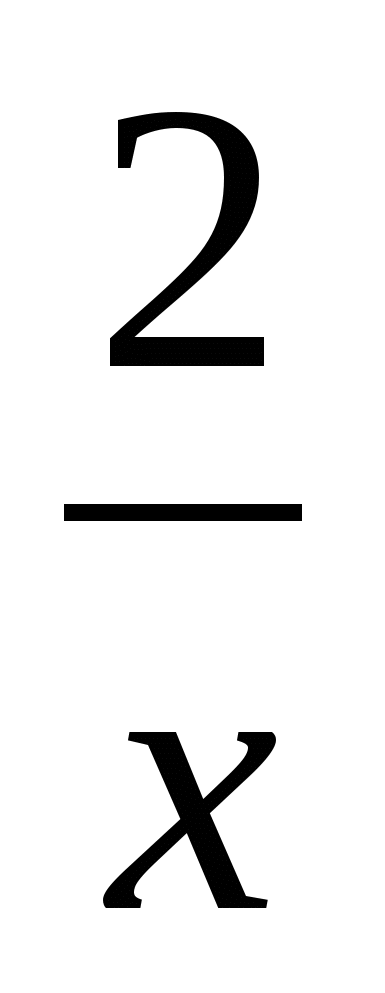 -
-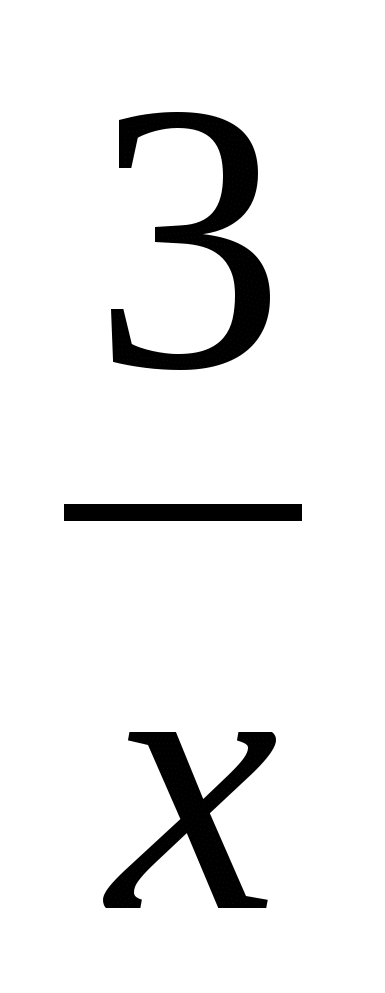 =25; 4)
=25; 4) 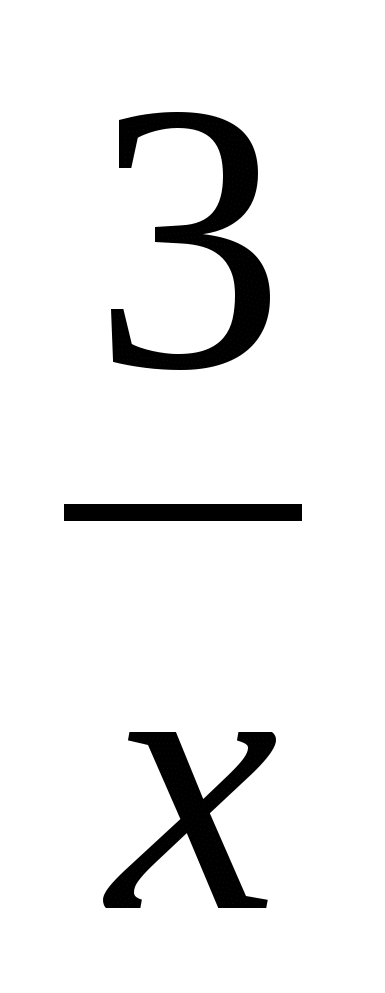 -
-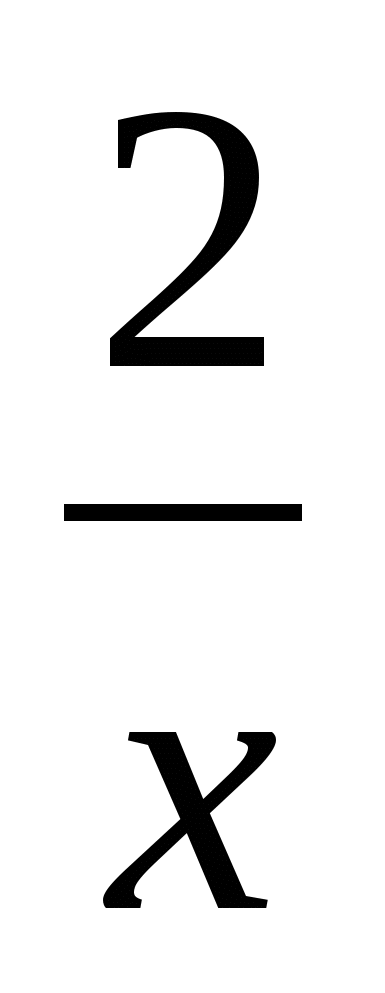 =25.
=25.
9. Решите неравенство: 3(3х-1)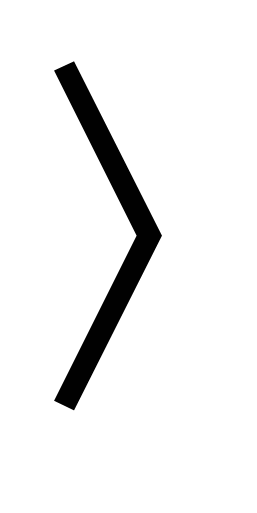 10х-14.
10х-14.
Ответ ________________
II часть
10. Укажите наибольшее целое число, принадлежащее решению неравенства -3х+х2-4≤0.
11. Решите графически систему уравнений:
у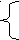 =
=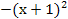 ;
;
у= х-1.
12. Решите задачу:
Бригада трактористов к определенному сроку должна была вспахать 1800 га. Ежедневно перевыполняя план на 25 га, уже за 4 дня до срока бригада не только выполнила задание, но и вспахала дополнительно 200 га. Сколько гектаров должна была ежедневно вспахивать бригада по плану?
13. Постройте график функции у=|х-2|-3.
С помощью графика найдите:
а) наименьшее значение функции;
б) промежутки возрастания, убывания функции;
в) значения х, при которых у=0, у>0,у<0;
г) множество значений функции.
Вариант II
I часть
1. Найдите значение выражения 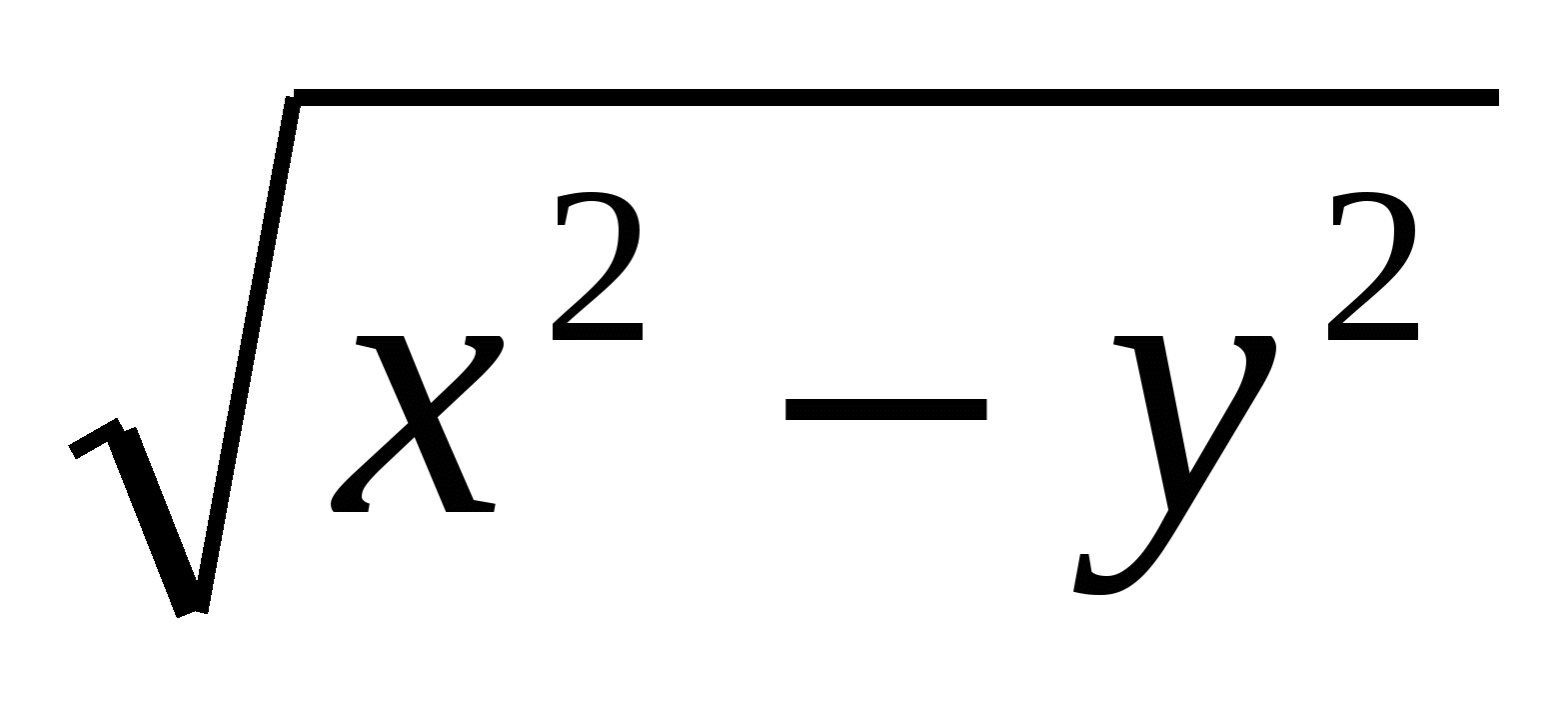 при х=10 и у= -6
при х=10 и у= -6
Ответ ________________
2. Упростите выражение а-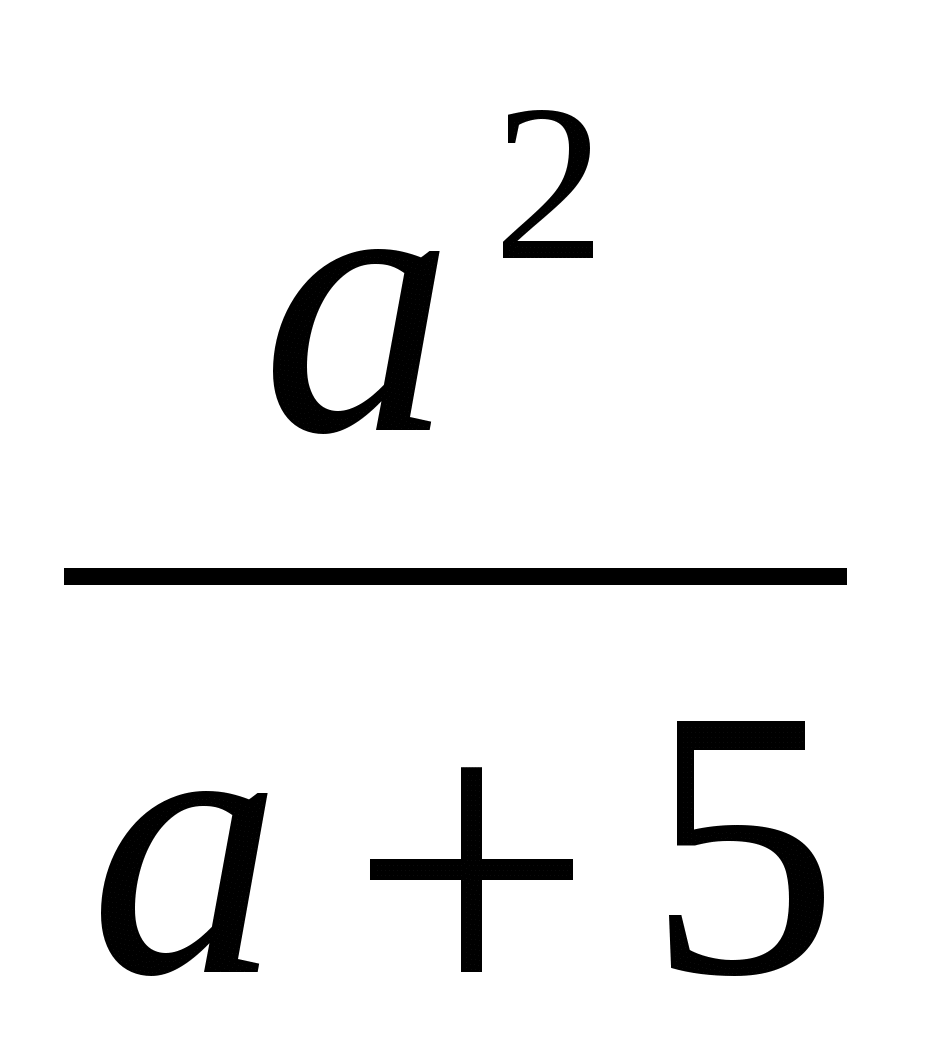 .
.
1) 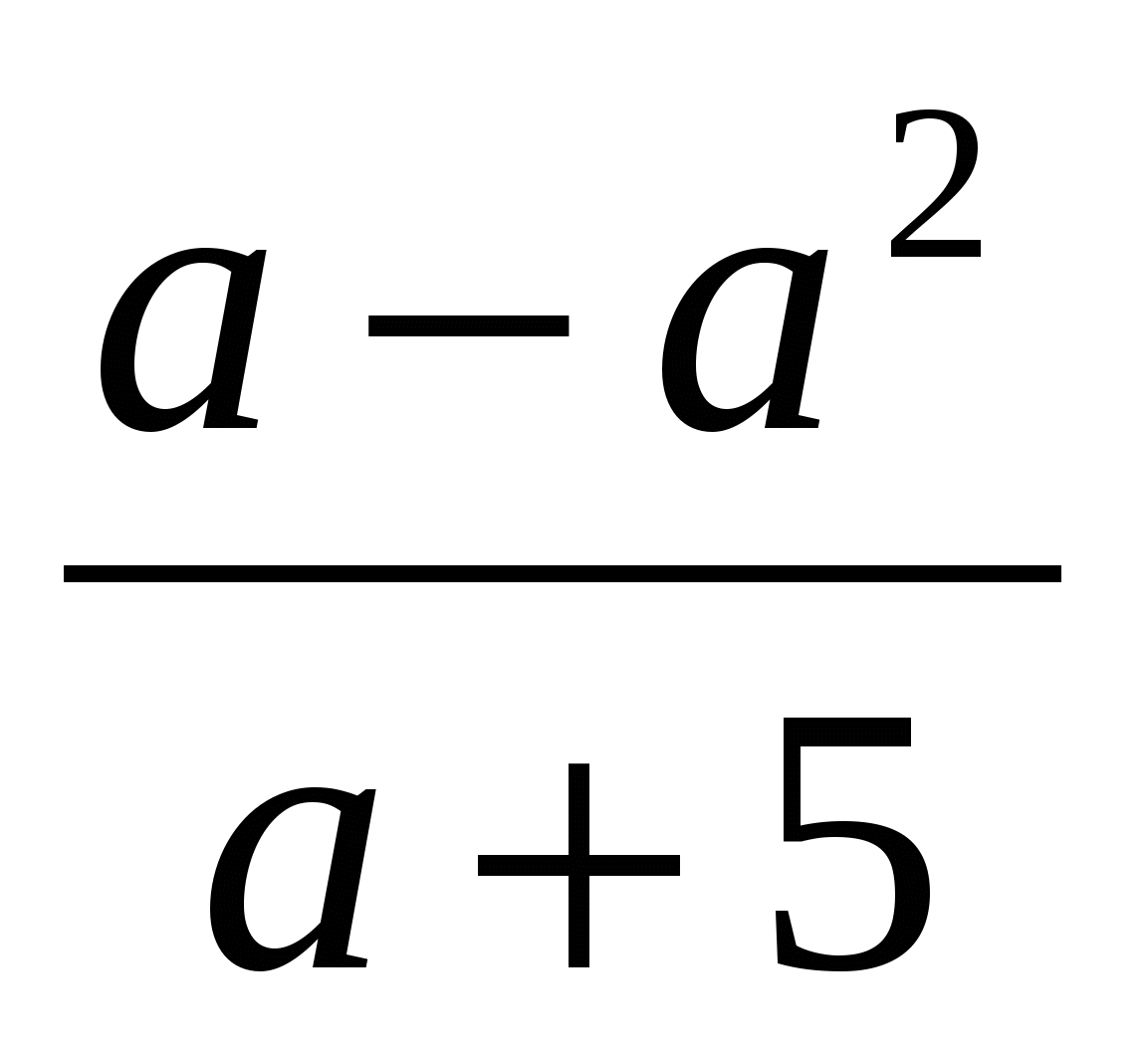 ; 2)
; 2) 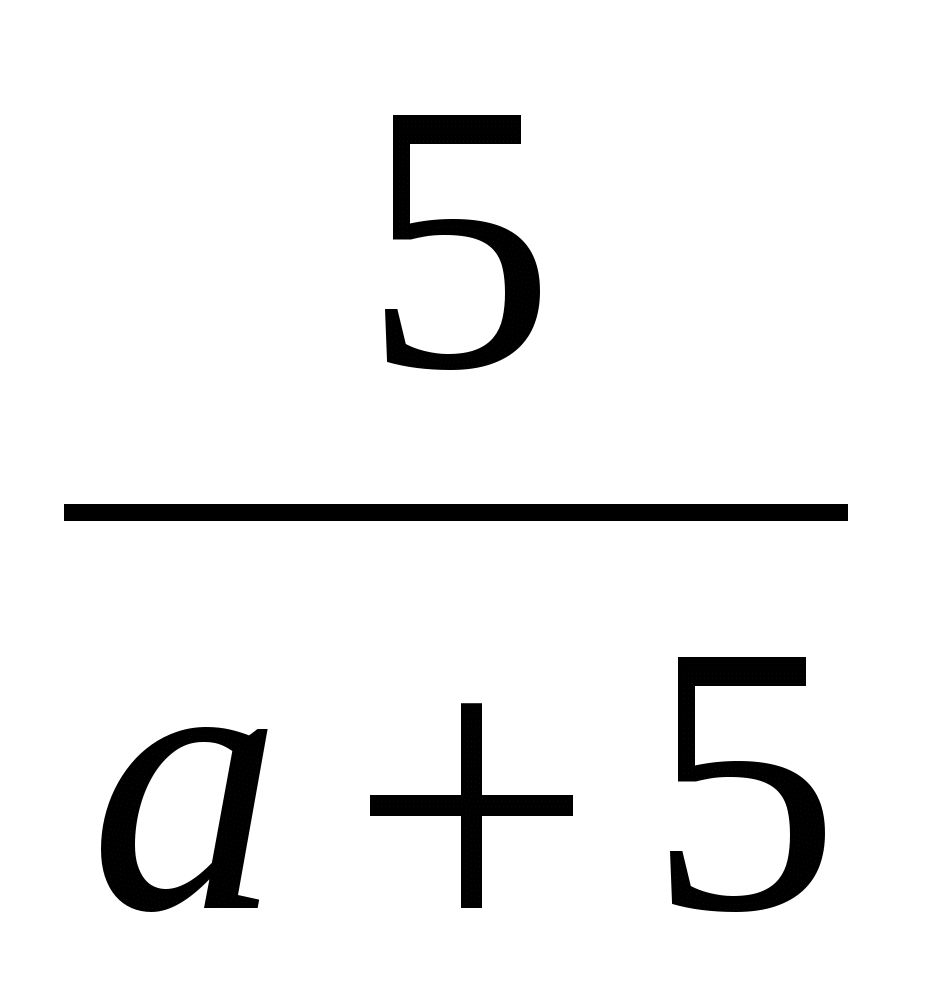 ; 3)
; 3) 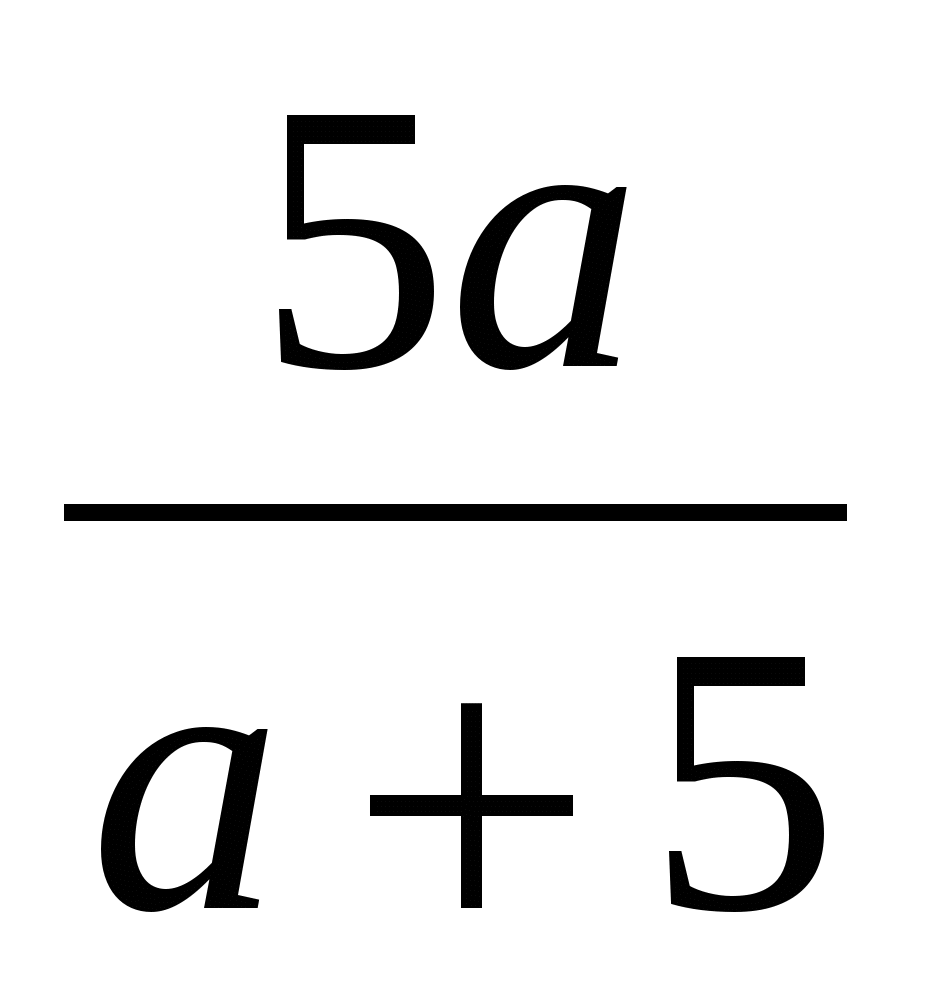 ; 4)
; 4) 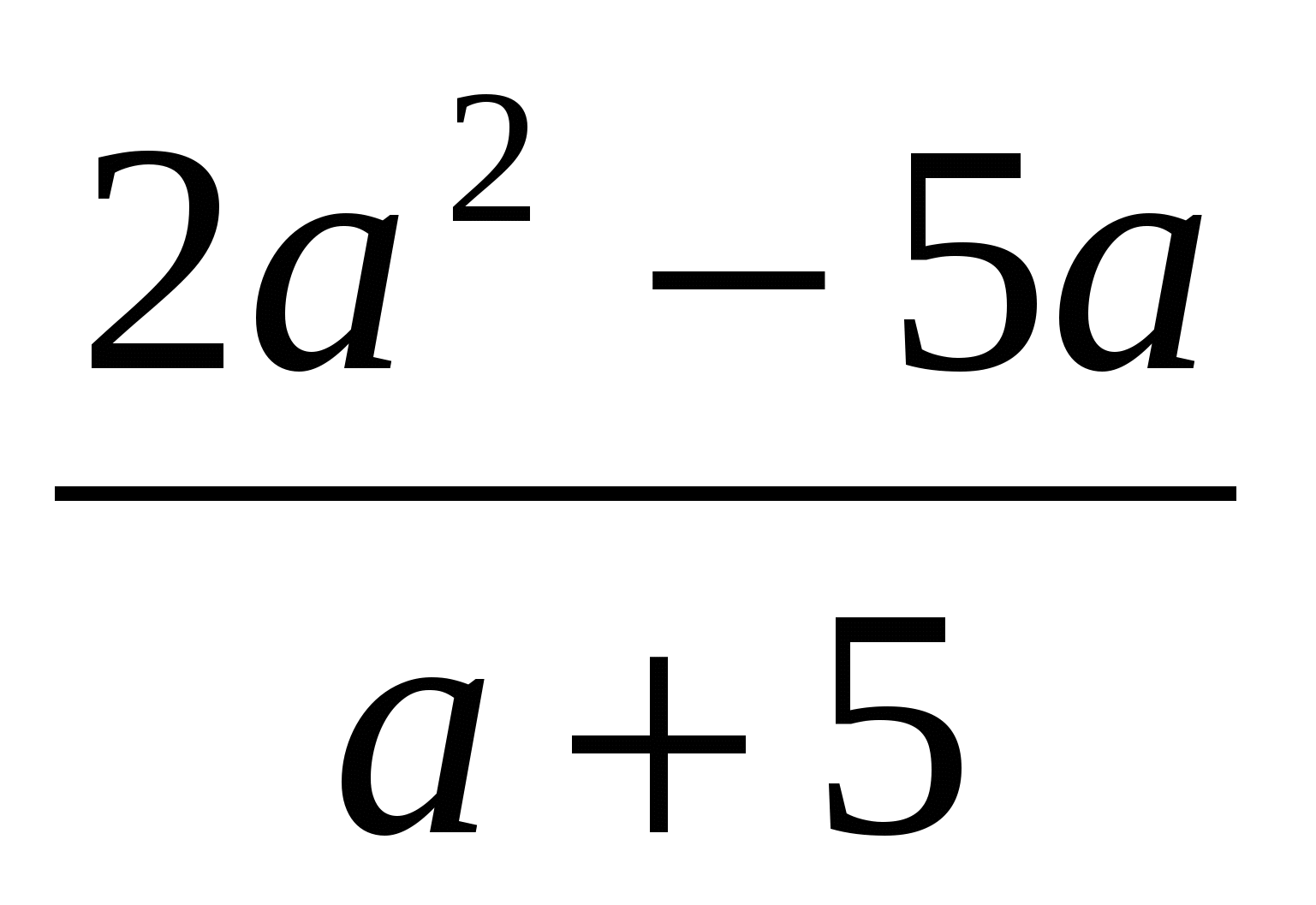 .
.
3. Решите уравнение: 3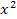 +8х-3=0
+8х-3=0
Ответ ________________
4. Для каждого выражения из верхней строки укажите равное ему выражение из нижней.
1) (с4с2)2; 2) (с3)2с4; 3) 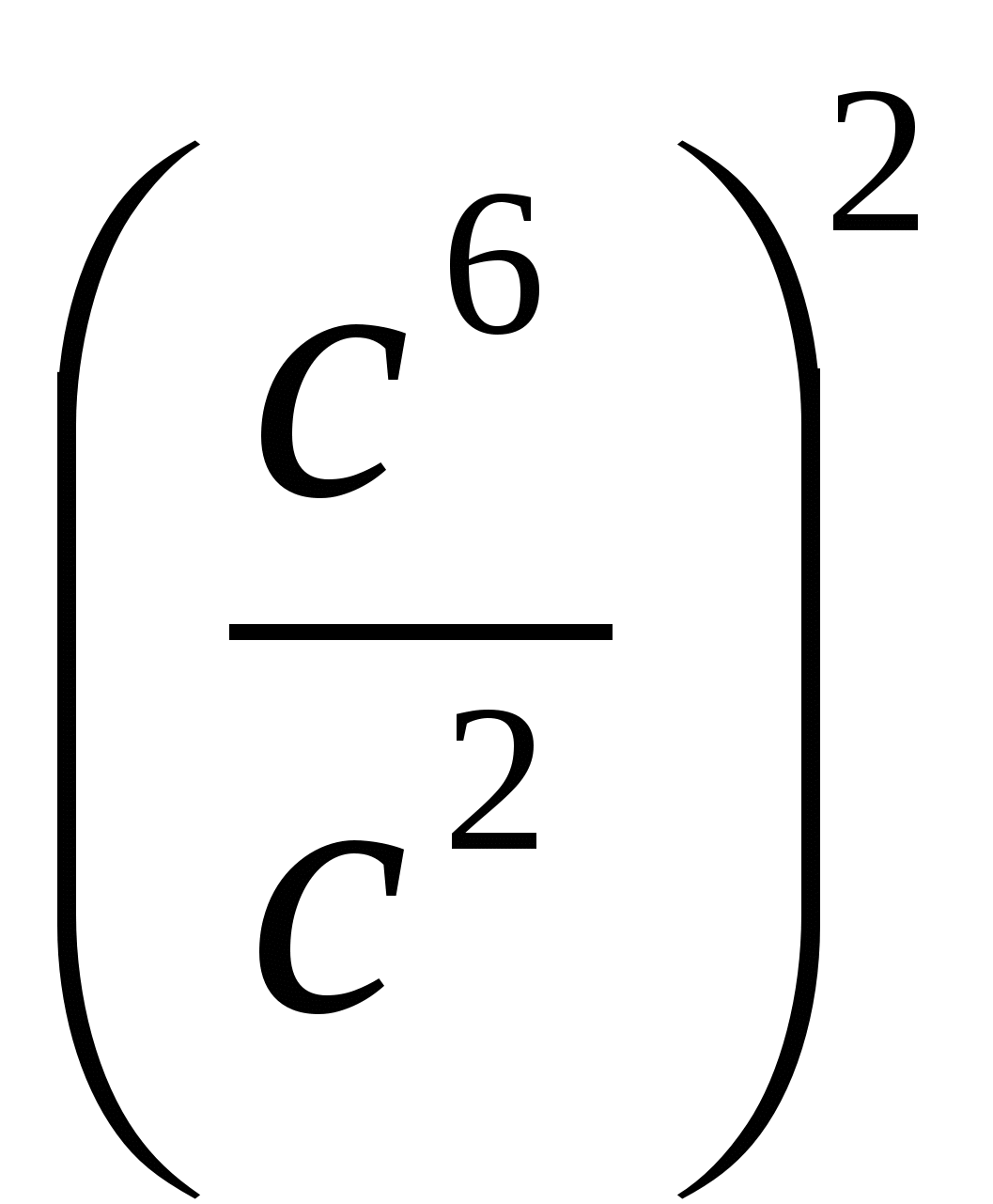
а) с6; б) с8; в) с10; г) с12
1
2
3
5. Функции заданы формулами: а) у=х2-1; б) у=х2+1; в) у=-х2-1; г) у=-х2+1.
Графики каких из этих функций не пересекает ось х?
1) б и в; 2) в и г; 3) а и г; 4) а и б.
.
6. Упростите выражение 4b(b+2)-(4+b)2.
Ответ _______________
7. Составьте квадратное уравнение, корнями которого являются числа х1=3; х2=5:
1) х2-8х+15=0; 2) х2+8х-15=0;
3) х2-8х-15=0; 4) х2+8х+15=0.
8. От дома до школы Коля обычно едет на велосипеде со скоростью 10 км/ч. Чтобы приехать в школу раньше на 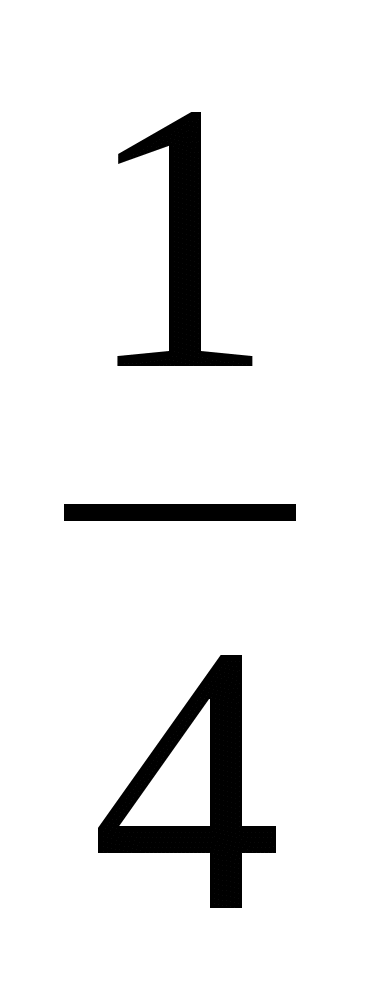 ч, ему надо ехать со скоростью 12 км/ч. Чему равно расстояние от дома до школы?
ч, ему надо ехать со скоростью 12 км/ч. Чему равно расстояние от дома до школы?
Пусть х км – расстояние от дома до школы. Какое уравнение соответствует условию задачи?
1) 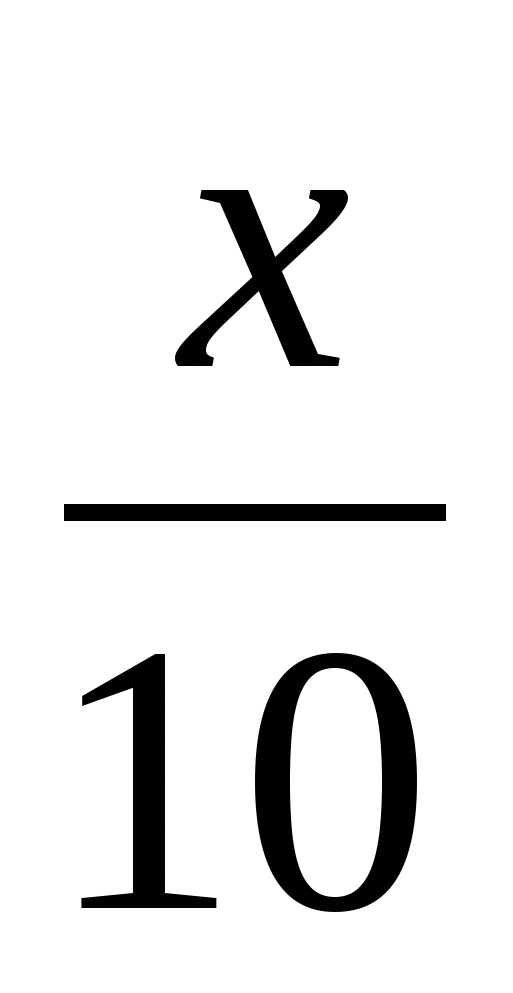 -
-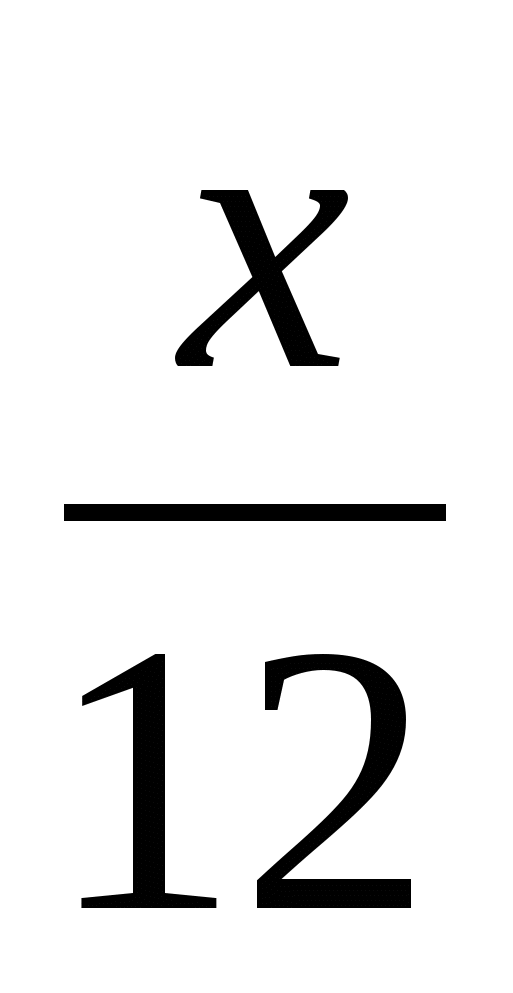 =
=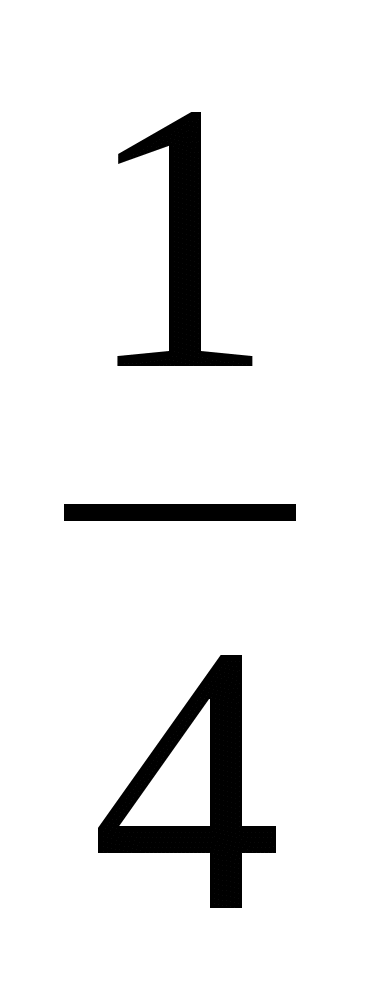 ; 2)
; 2) 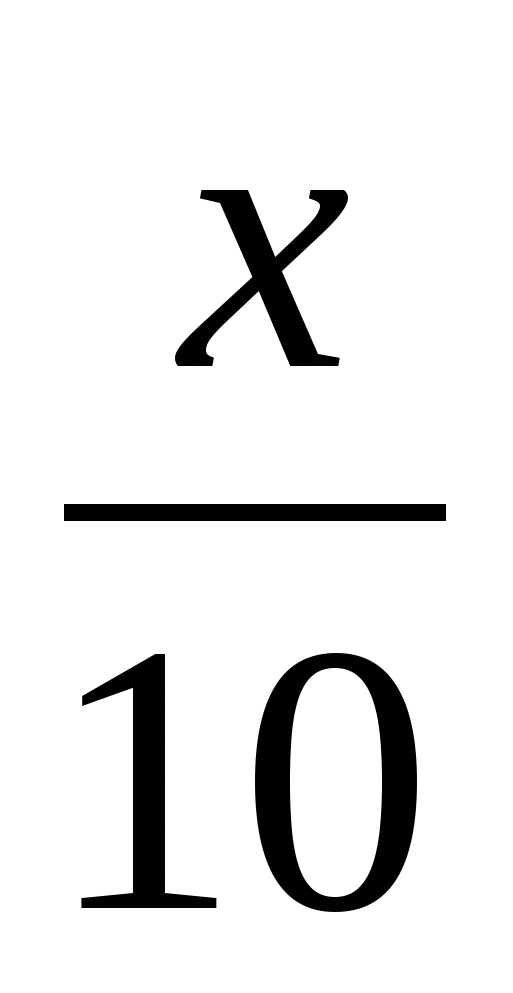 -
-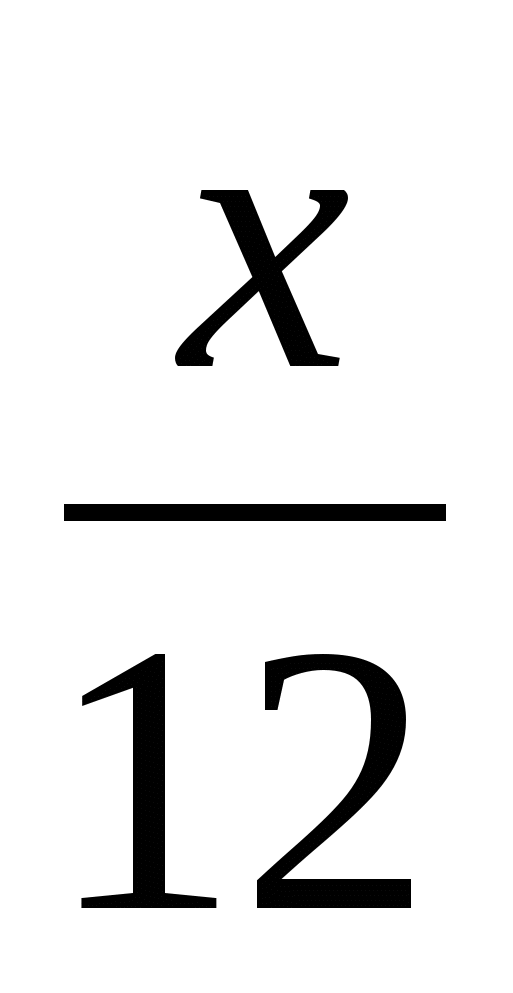 =15; 3)
=15; 3) 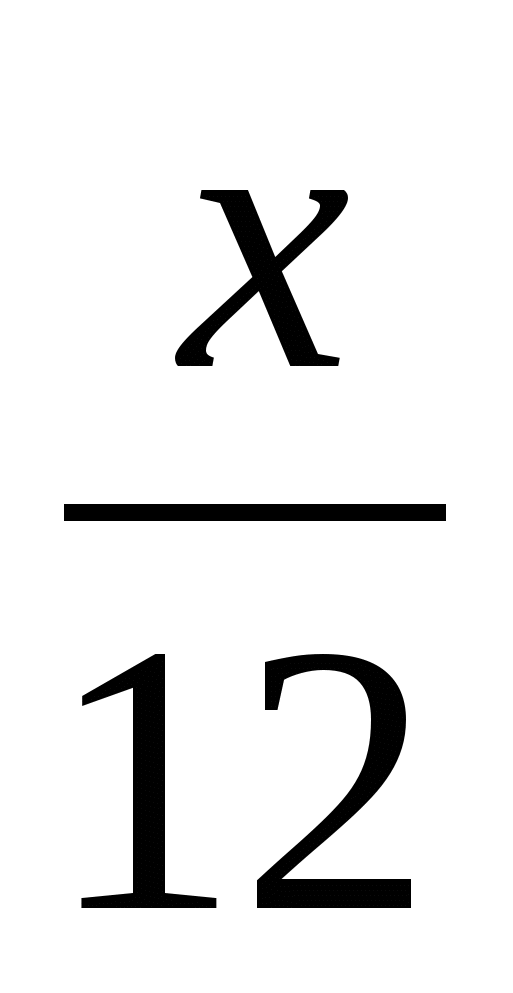 -
-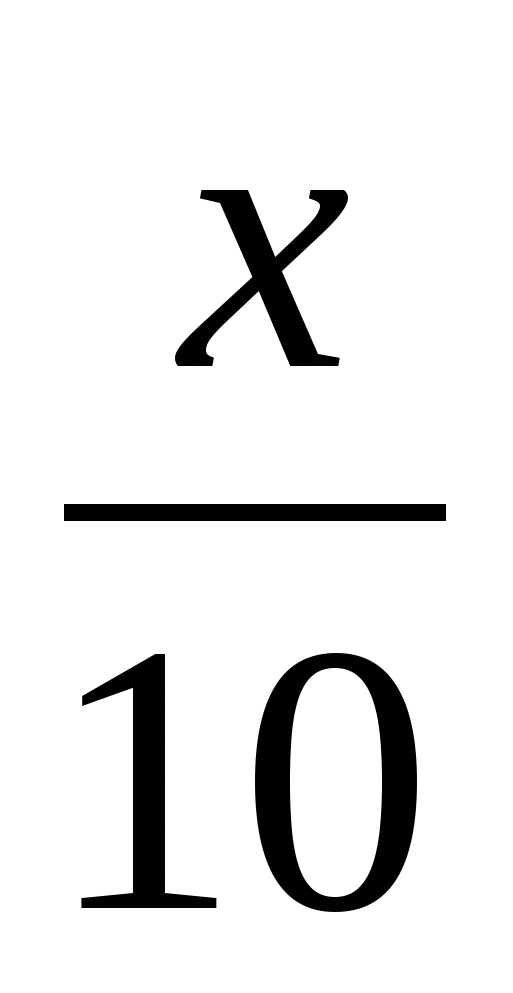 =
=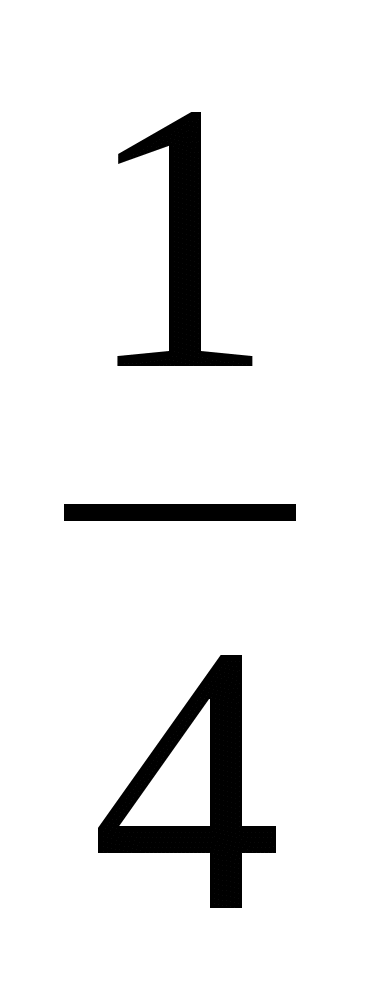 ; 4)
; 4) 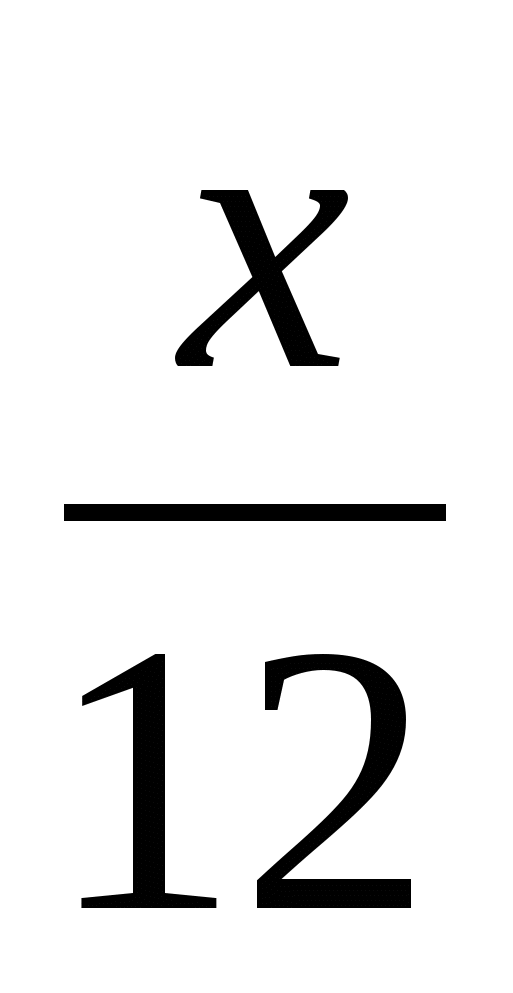 -
-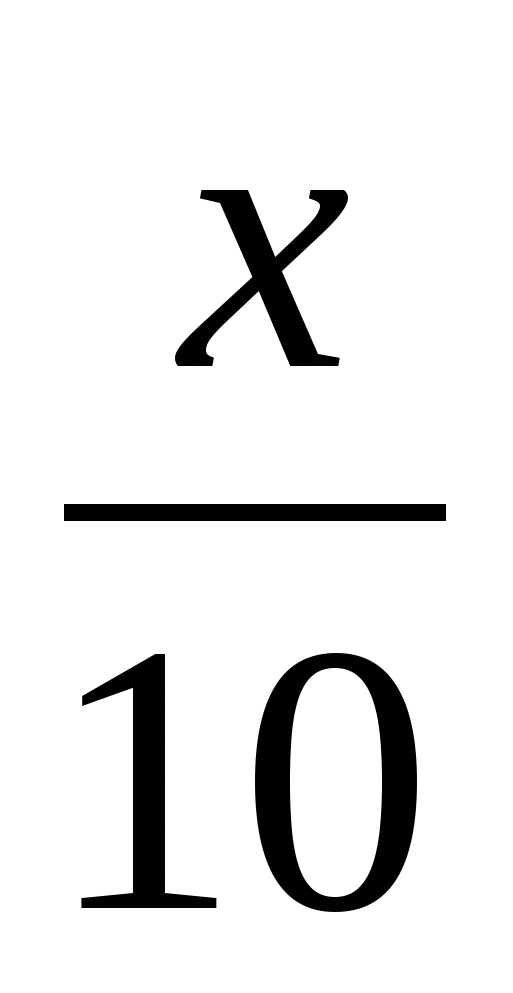 =15.
=15.
9. Решите неравенство: 5х+20<2(4х-5).
Ответ ________________
II часть
10. Укажите наименьшее натуральное число, принадлежащее решению неравенства
-3+х2--2х≤0.
11. Решите графически систему уравнений:
у =
=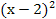 ;
;
у=х.
12. Решите задачу:
Для перевозки 180 туристов было заказано несколько автобусов. Однако два автобуса не прибыли, а туристов приехало на 8 человек больше, чем ожидалось. Поэтому пришлось в каждом автобусе разместить на 17 человек больше, чем требовалось. Сколько туристов было размещено в каждом автобусе?
13. Постройте график функции у=5-|х+2|.
С помощью графика найдите:
а) наибольшее значение функции;
б) промежутки возрастания, убывания функции;
в) значения х, при которых у=0, у>0,у<0;
г) множество значений функции.