





 Муниципальное бюджетное учреждение
Муниципальное бюджетное учреждение
средняя школа №82
г.о. Тольятти Самарской области
Тематическая разработка
«Внимание, параметр»
(различны методы решения задач с параметром)
Класс: 10 -11
Автор: Родионова Галина Михайловна,
учитель математики
МБУ СШ № 82 г.о. Тольятти
Самарской области
2014
Различные способы решения задач с параметрами
Задачи с параметром вызывают у многих если не панический страх, то по крайней мере, чувство неудобства. Между тем задачи с параметром можно одолеть различными способами. Покажем на примере несколько из них.
Задача 1. Найти все значения параметра а, при которых не имеет корни уравнение
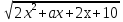 = x – 1. (1)
= x – 1. (1)
Решение: Данное уравнение равносильно ситстеме
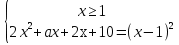
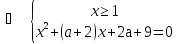
Уравнение (1) не имеет корней тогда и только тогда, когда не имеет решения эта система. Это возможно в двух случаях :
а) квадратное уравнение не имеет корней;
б) корни этого уравнения не удовлетворяют условию x ≥ 1.
Найдем все значения параметра, при котором выполняется хотя бы один случай:
а) уравнение 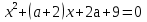 не имеет корней, если D < 0, т.е.
не имеет корней, если D < 0, т.е. 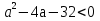 и, значит, a
и, значит, a 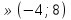 ,
,
б) корни уравнения 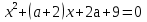 меньше 1.
меньше 1.
Рассмотрим три случая решения этой задачи:
1 способ. Корни уравнения меньше 1, если больший корень уравнения меньше 1(достаточное условие):
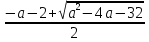 < 1
< 1 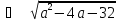 < a + 4
< a + 4 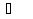
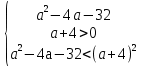
 a
a 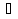 [8; + ∞ ).
[8; + ∞ ).
Объединяя ответа а) и б) получим ответ: a 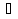 [- 4; + ∞ ).
[- 4; + ∞ ).
Ответ: a ϵ (- 4; + ∞ ).
2 способ решения (б). Рассмотрим квадратичную функцию
f (x) = 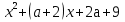 .
.
Её корни (нули функции) меньше 1 тогда и только тогда, когда одновременно выполняются условия: D 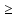 0, f(1) > 0, x0 < 1, где точка минимума данной функции (вершина параболы). Отсюда
0, f(1) > 0, x0 < 1, где точка минимума данной функции (вершина параболы). Отсюда
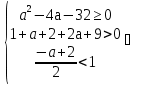 a
a 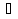 [8; + ∞ ).
[8; + ∞ ).
3способ. Пусть t = x – 1. Тогда x < 1 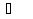 t +1 < 1
t +1 < 1 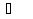 t < 0. В таком случае уравнение примет вид
t < 0. В таком случае уравнение примет вид
t2 + (a +4) t + 3a +12 = 0.
Корни уравнения отрицательны, если их сумма отрицательна, а произведение положительно. По теореме Виета заключаем:
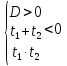
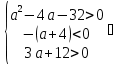 a
a 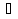 [8; + ∞ ).
[8; + ∞ ).
Объединяя ответа а) и б) получим ответ: a 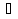 [- 4; + ∞ ).
[- 4; + ∞ ).
Ответ: a ϵ (- 4; + ∞ ).
4 способ . Возведем в квадрат обе части уравнения (1)
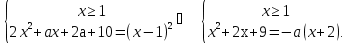
Последняя система позволяет графически найти все значения а, при которых система не имеет решения. Мы ищем все такие значения параметра а. при которых прямые пучка = - a (x + 2) на имеют общих точек с параболой
у = х2 +2х + 9 на промежутке [1;+ ∞). Для прямой у = 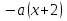 угловой коэффициент равен - а0 . Прямая и парабола имеют общие точки на промежутке [1; +∞) при а
угловой коэффициент равен - а0 . Прямая и парабола имеют общие точки на промежутке [1; +∞) при а 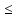 a0 . При a > a0 общих точек нет (сделай рисунок). Значение a0 найдем из того условия, что прямая у =
a0 . При a > a0 общих точек нет (сделай рисунок). Значение a0 найдем из того условия, что прямая у = 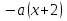 проходит через точку М(1;12), а0 = - 4.
проходит через точку М(1;12), а0 = - 4.
Ответ: а > - 4.
Возможна и несколько иная графическая интерпретация. Из уравнения (1) получим систему:
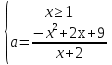
Далее находим, при каких значениях параметра а прямая у = а не имеет общих точек с графиком функции у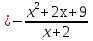 .
.
График можно построить, применяя производную.
Задача 2. Найти все значения параметра а , при которых уравнение
a |x - 1| = x + 2 имеет ровно один корень . Укажите этот корень.
Решение:
Если х 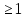 , то x =
, то x = 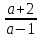 . Преобразуем эту дробь: x =
. Преобразуем эту дробь: x = 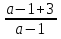 = 1 +
= 1 + 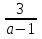 . Отсюда видно, что x > 1 при a >1.
. Отсюда видно, что x > 1 при a >1.
Если x < 1, то исходное уравнение примет вид a(1 – x) = x + 2 . Отсюда
x = 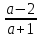 . Эта дробь меньше 1 при a > - 1.
. Эта дробь меньше 1 при a > - 1.
Изобразим найденные значения а на координатной прямой.
а
- 1 1
По рисунку видны два случая. В первом случае при а > 1 уравнение имеет два корня: x = 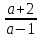 и x2 =
и x2 = 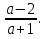
Промежуток а 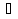 (1; + ∞) показан двойной «штриховкой». Второй случай показан одной «штриховкой». При a
(1; + ∞) показан двойной «штриховкой». Второй случай показан одной «штриховкой». При a 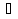 (-1 ; 1] имеет один корень. Подчеркнём, что а = 1 относится ко второму случаю, а в первом исключается.
(-1 ; 1] имеет один корень. Подчеркнём, что а = 1 относится ко второму случаю, а в первом исключается.
Ответ: при a 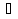 (-1; 1] один корень x =
(-1; 1] один корень x = 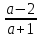 .
.
Задача 3 . Найти все значения параметра а , при которых уравнение
x4 + (3a + 1) x2 + a +3 = 0 имеет ровно четыре различных действительных корня .
Решение: Введем обозначение х2 = у и запишем данное уравнение в виде
у2 + (3а + 1)у + а +3 = 0.
Из условия х2 = у следует, что у 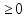
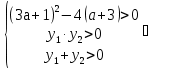
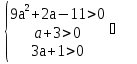 -3 < a < -
-3 < a < - 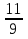 .
.
Ответ: a 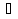 (- 3; - 1
(- 3; - 1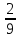 ).
).
Задача 4. Найти все значения параметра а , при которых уравнение
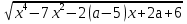 = x2 – 4 имеет хотя бы один корень . Решение:
= x2 – 4 имеет хотя бы один корень . Решение:
данное уравнение равносильно системе :
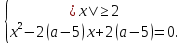
Первое условие не выполняется при х 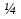 (-2; 2). Условие второе не выполняется в двух случаях. Первый: уравнение не имеет корней, т.е. дискриминант D меньше 0.Тогда
(-2; 2). Условие второе не выполняется в двух случаях. Первый: уравнение не имеет корней, т.е. дискриминант D меньше 0.Тогда 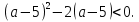 Отсюда
Отсюда
a 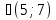 . Второй случай: уравнение системы имеет корни, но не те, что требуются, они не удовлетворяют условию
. Второй случай: уравнение системы имеет корни, но не те, что требуются, они не удовлетворяют условию 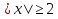 , т.е. принадлежат интервалу (-2; 2). Этот случай опишем системой неравенств, обозначив через f(x) подкоренное выражение в исходном уравнении :
, т.е. принадлежат интервалу (-2; 2). Этот случай опишем системой неравенств, обозначив через f(x) подкоренное выражение в исходном уравнении :
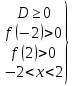
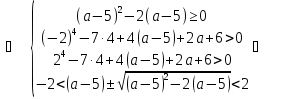
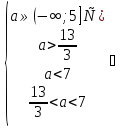
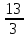 < a
< a 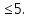
Поскольку a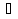 (
(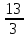 ;
; 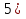
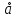 (
(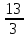 ;
; 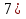 , утверждаем, что при a
, утверждаем, что при a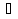 (
(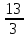 ;
; 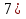 решений нет. Значит, при всех других значениях а решение есть.
решений нет. Значит, при всех других значениях а решение есть.
Ответ: a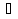 (-
(- 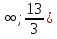
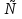 [
[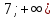 .
.
Задача 5. Найти все значения параметра а, при которых уравнение
(a - 3) 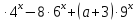 = 0 не имеет корней.
= 0 не имеет корней.
Решение:
Путем замены y = ( 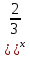 (где у >0) приведем данное уравнение к виду
(где у >0) приведем данное уравнение к виду
(a - 3) 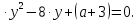
Если в последнем уравнении а =3, то у = 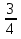 > 0,
> 0, 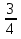 = (
= ( 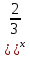 – это уравнение имеет корень.
– это уравнение имеет корень.
Если в последнем уравнении, а 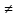 3, то исходное уравнение не имеет корней в двух случаях:
3, то исходное уравнение не имеет корней в двух случаях:
а) когда дискриминант D уравнения отрицателен;
б) когда у1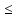 у2
у2 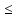 0. Рассмотрим каждый случай.
0. Рассмотрим каждый случай.
а) D < 0, 25 – a2 5, либо a < - 5;
б)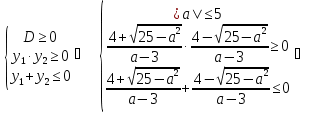
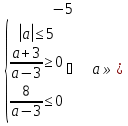 ; - 3].
; - 3].
Объединяя случаи а) и б), получим : а 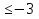 или а > 5.
или а > 5.
Ответ: 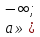 - 3]
- 3]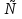 [5; +
[5; + 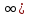 .
.
Список использованной литературы:
Алгебра и начала анализа 10: учебник для общеобразоват. учреждений Колягин Ю. М., Сидоров Ю.В., Ткачева М.В, Федорова Н. Е.: –М.: Мнемозина, 2011
Журнал «Математика в школе» 1998 №3, стр.9
Отличник ЕГЭ. Математика. Решение сложных задач: ФИПИ.-М. Интеллект- Центр, 2012.