Тест для 9 класса по алгебре
для проведения дифференцированного итогового зачета
по темам «Функция и ее свойства. Квадратный трехчлен и его корни.
Квадратичная функция и ее график».
Цель: установление уровня сформированности предметных, метапредметных и личностных результатов обучающихся по данной теме.
Инструкция по выполнению работы
На выполнение всей работы отводится 45 минут.
Работа состоит из 11 заданий. Среди них 9 заданий с выбором одного верного ответа из четырех предложенных (задания 1-9) и 2 задания, требующее подробное решение (задания 10,11).
Задания 1 -9. К каждому заданию приводится 4 варианта ответа, один из которых верный. За каждое верно выполненное задание выставляется один балл.
Задания 10, 11 предусматривают подробное решение. Максимальный балл за задание 3.
Максимальное количество баллов за всю работу – 15.
Критерии оценки тестовых заданий
Оценка «отлично»
Правильно выполнены все задания или допущена 1 вычислительная ошибка в заданиях 10 или 11, или 11задание выполнено наполовину
14 –15 баллов
Оценка «хорошо»
46 – 85 % правильных ответов
7 – 13 баллов
Оценка «удовлетворительно»
26 – 45 % правильных ответов
4– 6 баллов
Оценка «неудовлетворительно»
25% или менее 4 правильных ответов (задания 1-9)
0 – 3 балла
Вариант 1
1.Какова область определения функции?
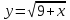а) [-9;+∞);
б) (-∞;-9];
в) (-9;+∞);
г) (-∞;-9).
y
2.График какой функции изображен на рисунке?0
а) y= -x2-14
б) y= -x2+1;
x
1
-1
в) y= x2+1;
-1
г) y= x2-1.
3.Функция задана формулой
f(x)= -x2+1.
Найдите f(4).
а) -15; в) -3;
б) 174 г) 5.
4.Укажите область значений функции
y=121-x2
а) (-∞;+∞); в) (-∞;121];
б) [-121;121]; г) [-11;11].
5.Функция задана графически.
y
Укажите промежутки убывания функции:
3
0
2
-1
x
1
-3
-1
а) [-3;1]; в) [-1;0];
б) [-3;0]; г) [0;1].
6.Найдите координаты вершины параболы
y=6x-x2
а) (6;0); в) (3;9);
б) (-3;-9); г) (0;6).
7. Какой квадратный трехчлен имеет 2 корня?
а) 4x2-4x+1; в) 2x2-x-3;
б) 3x2+2; г) 3x2-2x+1.
y
8. По графику функции y=ax2+bx+c определите знаки дискриминанта D и коэффициента а
0
б0;D<0;
x
в) a<0;D<0; г) a<0;D>0.
9. Сколько нулей имеет функция, график которой изображен на рисунке?
y
0
x
-2
4
7
а) 1; б) 4; в) 2; г) 3.
10.Решите неравенство:
x2≤9
11.Сократите дробь:
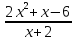
Вариант 2
1.Какова область определения функции?
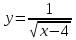а) (4;+∞);
б) [4;+∞);
в) (-∞;4);
г) (-∞;4].
2.График какой функции изображен на рисунке?
y
а) y=(x-1)2
x
-1
0
г) y= x2-1.
3.Функция задана формулой
f(x)=2-x2 .
Найдите f(-1).
а) 3; в) 0;
б) 1; г)-1.
4.Укажите область значений функции
y=49-x2
а) (-∞;+∞); в) (-∞;49];
б) [-7;7]; г) [-49;49].
5.Функция задана графически
y
Укажите промежутки возрастания функции:
0
x
4
-2
1
-1
а) [-1;4]; в) [-1;1];
б) [0;4]; г) [-2;-1]U[1;4].
6.Найдите координаты вершины параболы
y= -x2-4x+1
а) (-2;5); б) (2;-3); в) (4;1); г) (0;1).
7.Какой квадратный трехчлен не имеет корней?
а) 4x2-3x; в) x2+4x+3;
б) 9x2+6x+1; г) 5x2-x+1.
y
8. По графику функции y=ax2+bx+c определите знаки дискриминанта D и коэффициента аа) a<0;D>0
б0;D<0
в) a<0;D<0
0
x
г0;D>0
9. Сколько нулей имеет функция, график которой изображен на рисунке?
0
x2>4x
11. Сократите дробь:
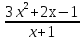
-4
-3
а)1 б)3 в)5 г)4
2
10.Решите неравенство:
x
y
4
Ответы к заданиям:
Номер
задания
1
2
3
4
5
6
7
8
9
10
11
1 вариант
а
г
а
в
в
в
в
б
б
[-3;3]
2х-3
2 вариант
а
б
б
в
б
а
г
а
в
(-∞;0)U(4;+ ∞)
3х-1