Тест за первое полугодие 11 класс алгебра
2 вариант
1. Вычислите : 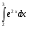 .
.
A) 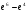 . B)
. B) 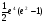 . C)
. C) 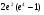 . D)
. D) 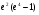 .
.
E) 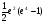 .
.
2. Вычислите: 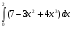 .
.
A) 11. B) 24. C) 16. D) 14. E) 22.
14. E) 22.
3. Вычислите: 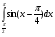 .
.
A) 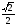 . B)
. B) 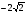 . C)
. C) 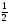 . D)
. D) 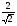 . E)
. E) 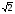 .
.
4. Вычислите:  .
.
A) 18,5. B) 18,25. C) 18,5. D) 18,75. E) 18.
18,75. E) 18.
5. Вычислите:  .
.
A) 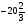 . B)
. B) 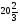 . C)
. C) 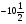 . D)
. D) 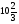 . E)
. E)  .
.
6. Вычислите: 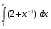 , где
, где  .
.
A) 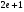 . B)
. B) 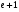 . C)
. C) 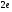 . D)
. D) 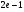 . E)
. E) 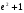 .
.
7. Вычислите площадь фигуры, ограниченной линиями: у= 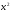 , у=0, х=2.
, у=0, х=2.
A) 2. B) 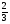 . C) 2
. C) 2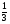 . D) 2
. D) 2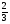 . E) 3.
. E) 3.
8. Вычислите площадь фигуры, ограниченной линиями: у= 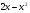 , у=0, х=2.
, у=0, х=2.
A) 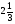 . B)
. B) 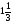 . C)
. C) 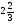 . D)
. D) 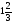 . E)
. E) 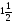 .
.
9. Вычислите площадь фигуры, ограниченной линиями: у=  , у=0, х=2.
, у=0, х=2.
A) 3. B) 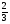 . C) 2. D)
. C) 2. D) 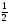 . E) 4.
. E) 4.
10. Найдите площадь фигуры, ограниченной линиями: у= 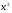 , у=0, х=1, х=2.
, у=0, х=1, х=2.
A)  . B)
. B) 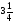 . C)
. C) 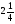 . D)
. D) 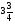 . E)
. E) 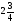 .
.
11. Найдите все первообразные для функции у(х) = х3−3х2+7х – 1.
A) 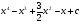 . B)
. B) 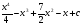 .
.
C) 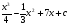 . D)
. D) 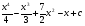 .
.  E)
E) 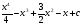 .
.
12. Какая из данных функций является первообразной для f(х)=  .
.
A) 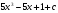 . B)
. B) 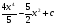 . C)
. C) 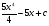 .
.
D) 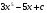 . E)
. E)  .
.
13. Найдите первообразную для функции у(х) = 3 – х3, график которой проходит
через точку (−2; −5)
A) 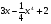 . B)
. B) 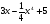 . C)
. C) 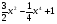 . D)
. D) 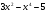 . E)
. E) 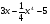 .
.
14. Функция F(х) = х4 – 4х2 + х +с является первообразной:
A) f(х)= 4х3−8х +1. B) u(х)= 4(х3−2) + 1. C) h(х)= 4х(х2 −2) + 1.
D) g(х)= 4х4−8х2+ 1. E) у(х)= 4(х4−2х +1).
15. Найдите первообразную функции 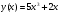 , значение которой равно
, значение которой равно 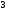 при
при
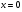 .
.
A) 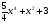 . B)
. B) 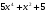 . C)
. C) 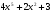 .
.
D) 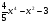 . E)
. E) 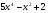 .
.
16. Найдите все первообразные для функции 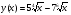 .
.
A) 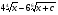 . B)
. B) 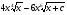 . C)
. C) 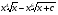 .
.
D)  . E)
. E) 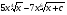 .
.
17. Найдите все первообразные для функции  , при всех
, при всех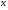 >0 .
>0 .
A)  . B)
. B) 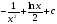 . C)
. C) 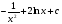 .
.
D) 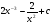 . E)
. E) 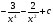 .
.
18. Найдите все первообразные для функции f(х)= 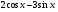 .
.
A) 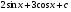 . B)
. B) 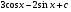 . C)
. C) 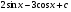 .
.
D) 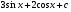 . E)
. E) 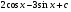 .
.
19. Найдите все первообразные для функции f(х)=  .
.
A) 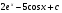 . B)
. B) 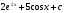 . C)
. C) 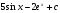 .
.
D) 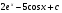 . E)
. E) 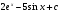 .
.
20. Найдите у′(0) + у′(1), если у(х) = 2х3 – 3х2 +5.
A) – 5 . B) 4. C) – 3 . D) 0. E) 3.
21. Дана функция у = 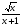 . Вычислите у′ (2).
. Вычислите у′ (2).
A) 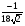 . B)
. B) 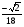 . C)
. C) 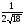 . D)
. D)  . E)
. E) 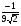 .
.
22 Дана функция у(x) =(4х+7)17, найдите у′(−2).
A) 68. B) – 86. C) – 68. D) 76. E) 67.
23. Решите неравенство у′(х)< 0, если у(х) = 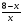 .
.
A) (0; +∞). B) (−∞; +∞). C) (−∞; 0). D) [−1; 1]. E) (0; 1).
24. Напишите уравнение касательной к графику функции у= 2х4 – х2 + 4 в точке с
абсциссой х0=−1.
A) у= 6х + 1. B) у – 2х+1=0. C) у +6х + 1=0. D) у= 1 – 6х. E) у= 1 – 2х
25. Напишите уравнение касательной к графику функции у= 2 –2 х2 в точке х0= 2.
A) у = − 8х + 10 B) у – 8х+10=0 C) у=10+6х. D) у + 6х+10=0. E) у = 10х – 8.