Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа №10
Урок алгебры для 7 класса
«Взаимное расположение графиков линейных функций»
Выполнила Марченко
Татьяна Григорьевна
учитель математики и физики
МОУ СОШ №10
2009г.
Тема: Взаимное расположение графиков линейных функций.
Тип урока: Урок изучения нового материала.
Технология: Личностно–ориентированная.
Цели урока :
Образовательные:
отработка навыков построения графиков функции вида y = kx +b;;
выяснение влияния значений k и b на положение графиков;
выяснение влияния значения параметра k на взаимное расположение графиков линейных функций.
Развивающие:
развитие познавательной активности;
развитие осмысленного отношения к своей деятельности;
развитие самостоятельности мышления: выделять главное, видеть общую закономерность и делать обобщенные выводы;
развитие культуры учебной деятельности.
Воспитательные:
воспитание аккуратности;
воспитание ответственного отношения к учению;
воспитание культуры общения.
Методы:
Наблюдение;
Эвристическая беседа;
Диалог;
Педагогической поддержки;
Создание ситуации успеха;
Проверка по образцу;
Формы: Фронтальный опрос, самостоятельная работа, индивидуальная работа.
Структура урока:
1.Организационный момент. (1 мин.)
2. Актуализация опорных знаний. (6 мин.)
3. Введение в тему. Постановка учебных задач. (3 мин.)
4. Ознакомление с новым материалом. (14 мин.)
5. Первичное осмысление и закрепление изученного. (10 мин.)
6. Рефлексия. (2мин.)
7. Домашнее задание. (2 мин.)
8. Итог. (2 мин.)
Ход урока:
1.Организационный момент.
Цель: Обеспечить рабочую обстановку на уроке, включить учащихся в учебную деятельность.
Учитель приветствует учащихся, проводит проверку готовности класса к уроку. Настраивает учащихся на работу.
2. Актуализация знаний.
Цель: Организовать познавательную деятельность учащихся.
Слайд №1. Задание 1.
График функции у = - 2х + 7 проходит через точку,
а) абсцисса которой - 3. Какова ордината этой точки?б) ордината точки равна – 3. Найти абсциссу точки. Открывается слайд № 2. Задание 2. Распределить данные функции по группам: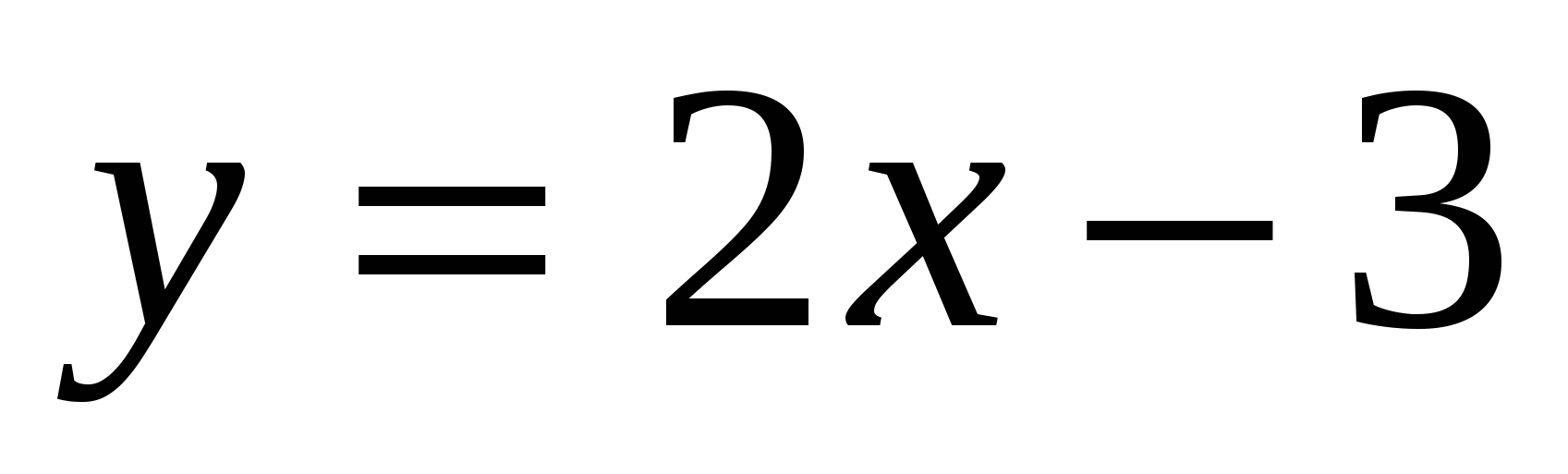 ;
; 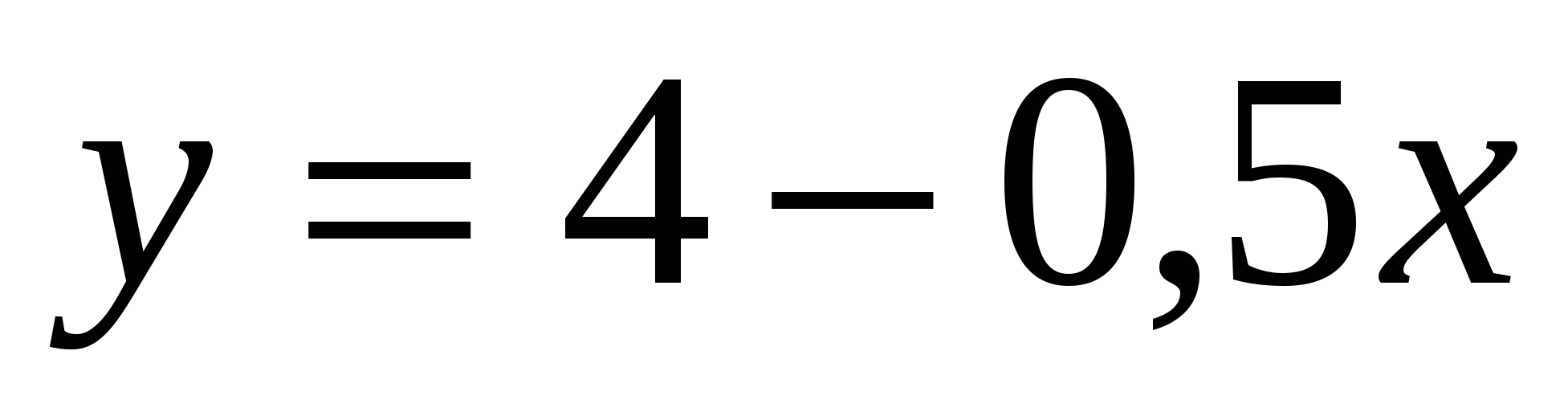 ;
; 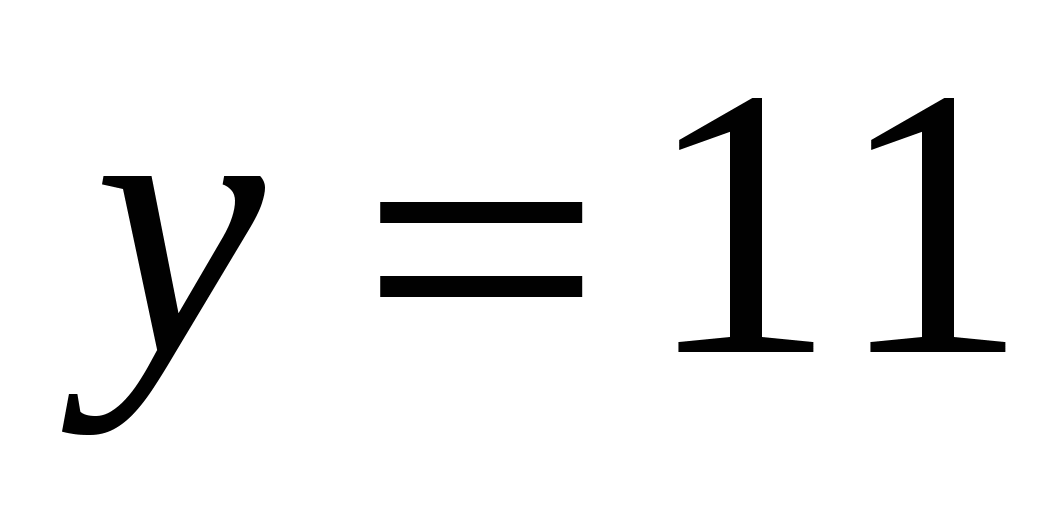 ;
; 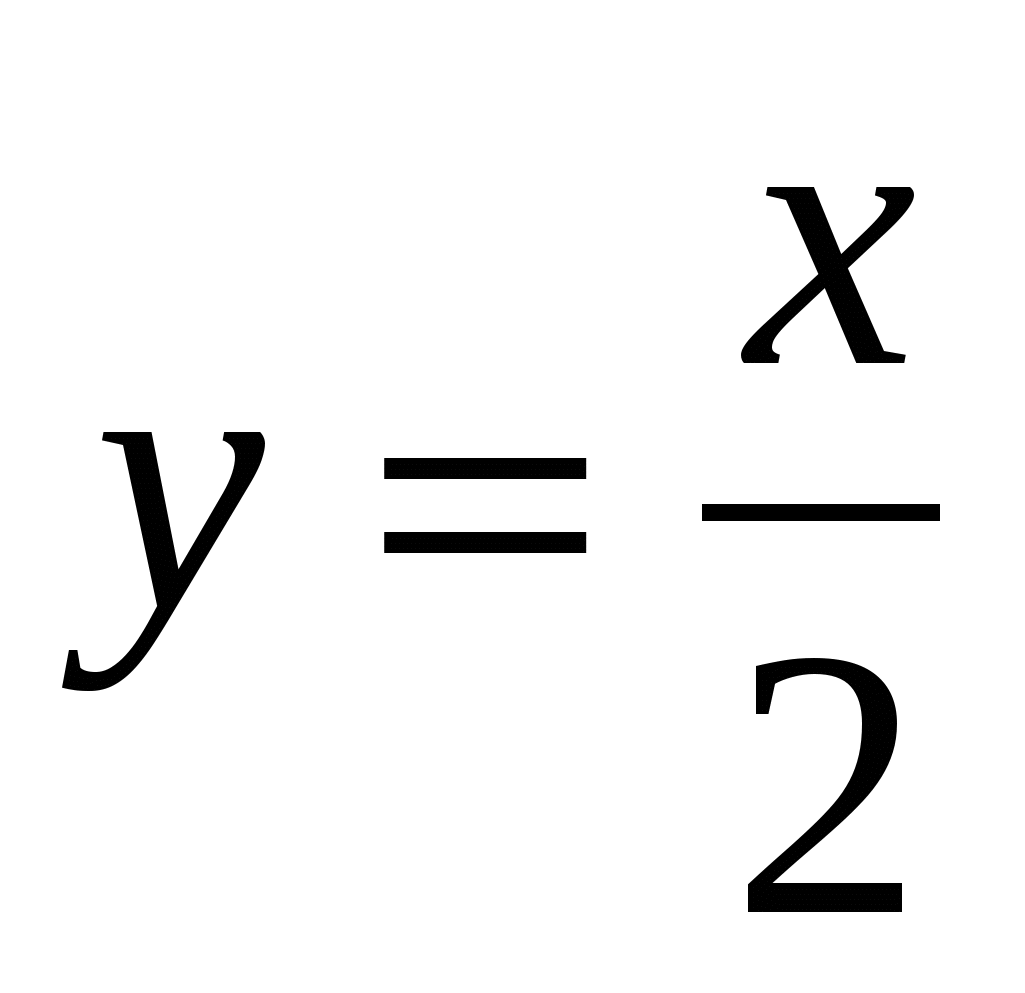 ;
; 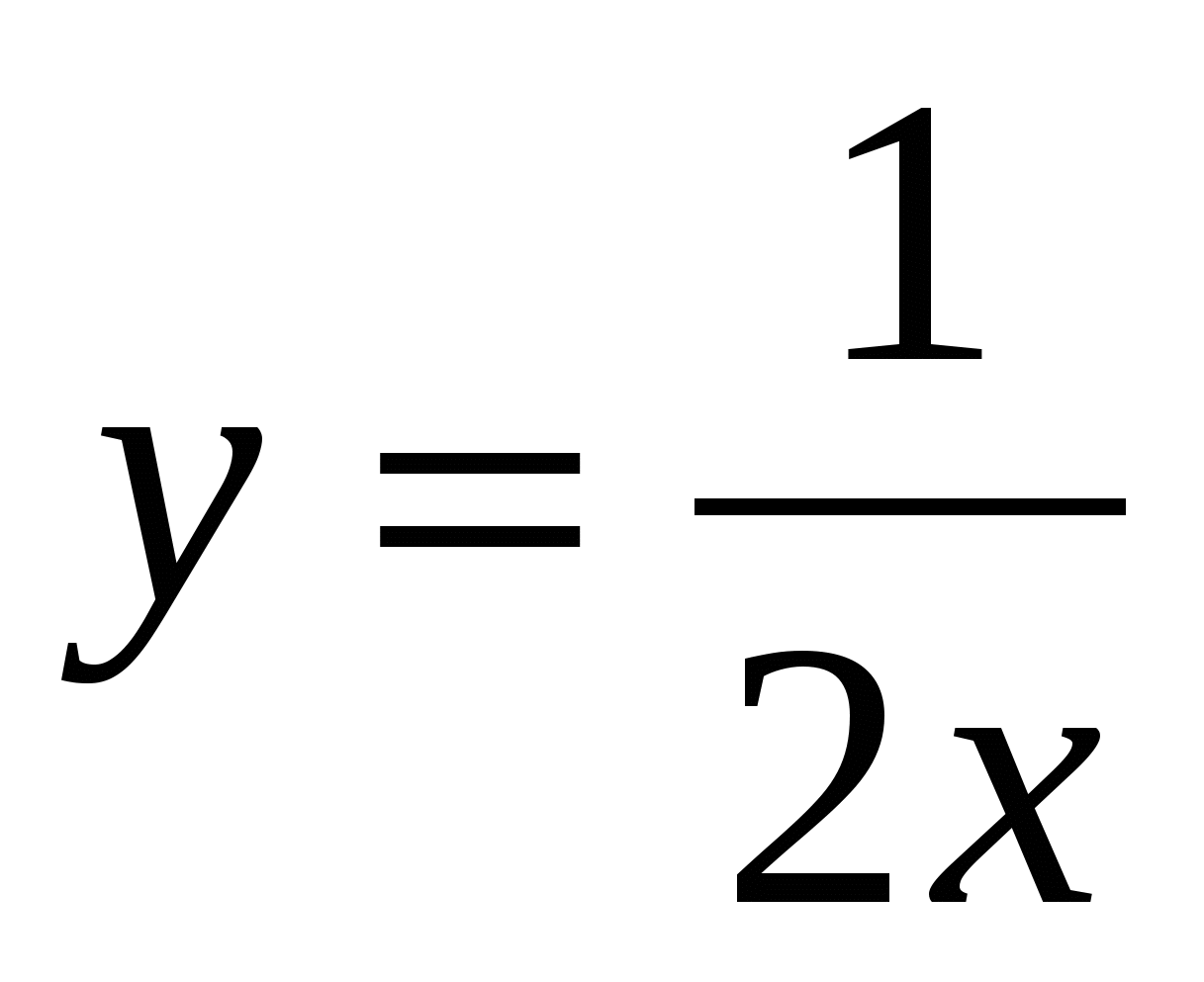 ;
; 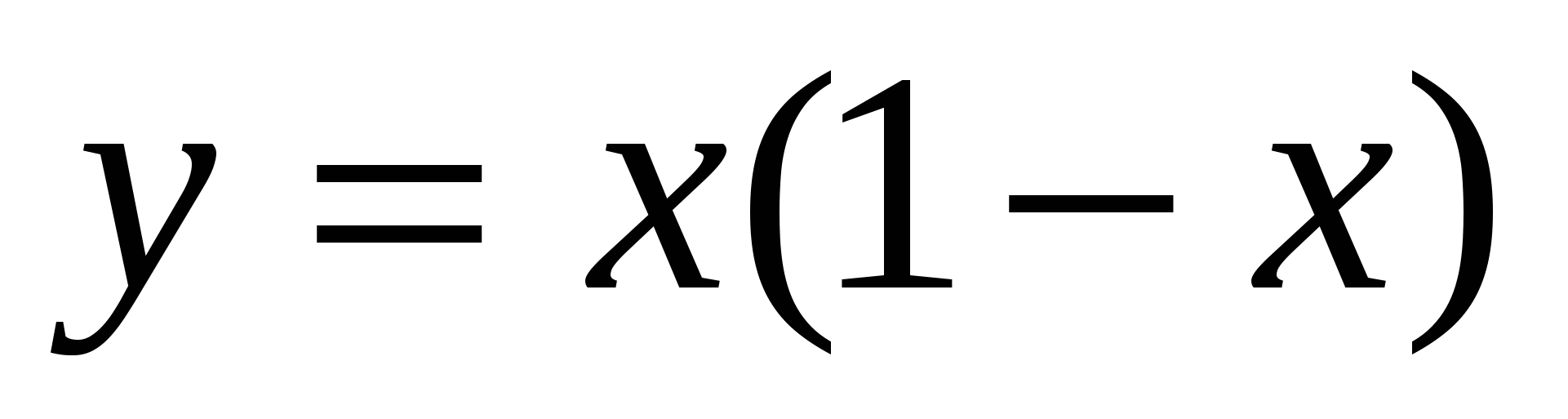 ;
;
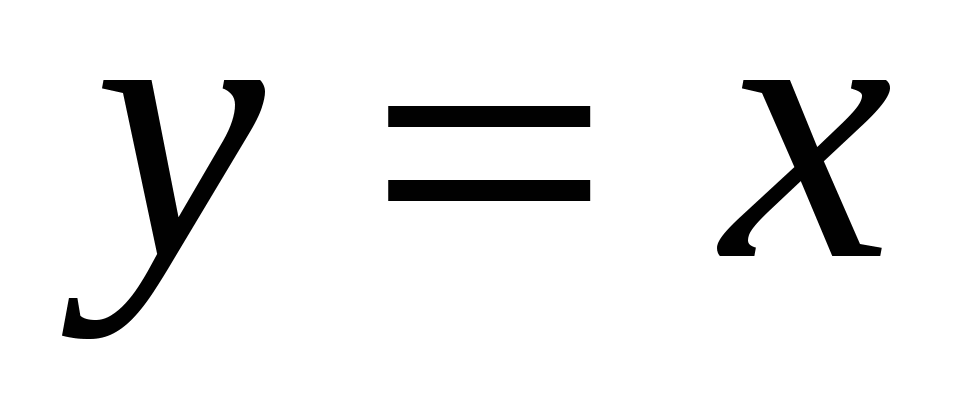 ;
; 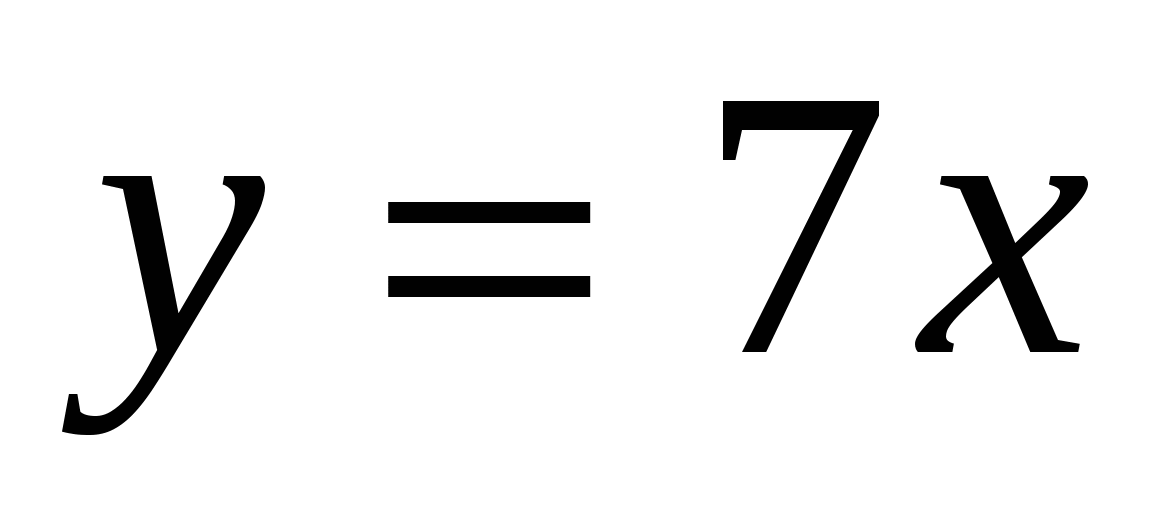 ;
; 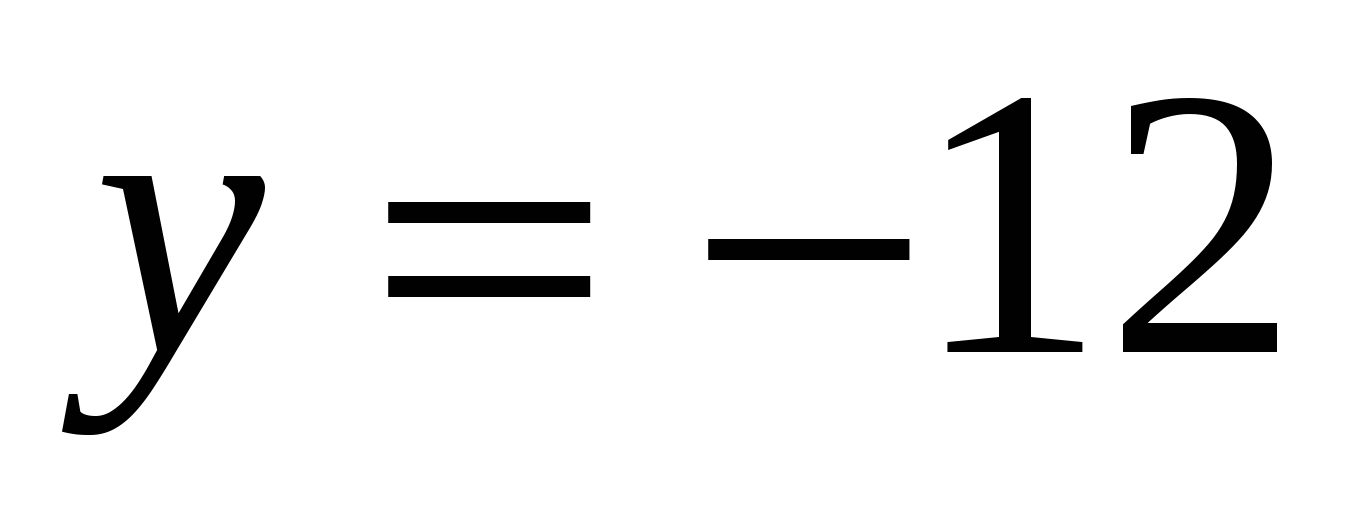 .
.
– На сколько групп вы распределили данные функции? (На две.)
– Какие функции отнесли к первой группе и почему? (Графиками данных функций являются прямые.)
Группы, указанные учащимися, учитель записывает на доске.
– Какие функции отнесли ко второй группе и почему?( Графиками данных функций не являются прямыми.)
– Обратите внимание на первую группу формул.
– Распределите данные функции на группы по их записи.
– На какие группы можем распределить данные функции?
1). 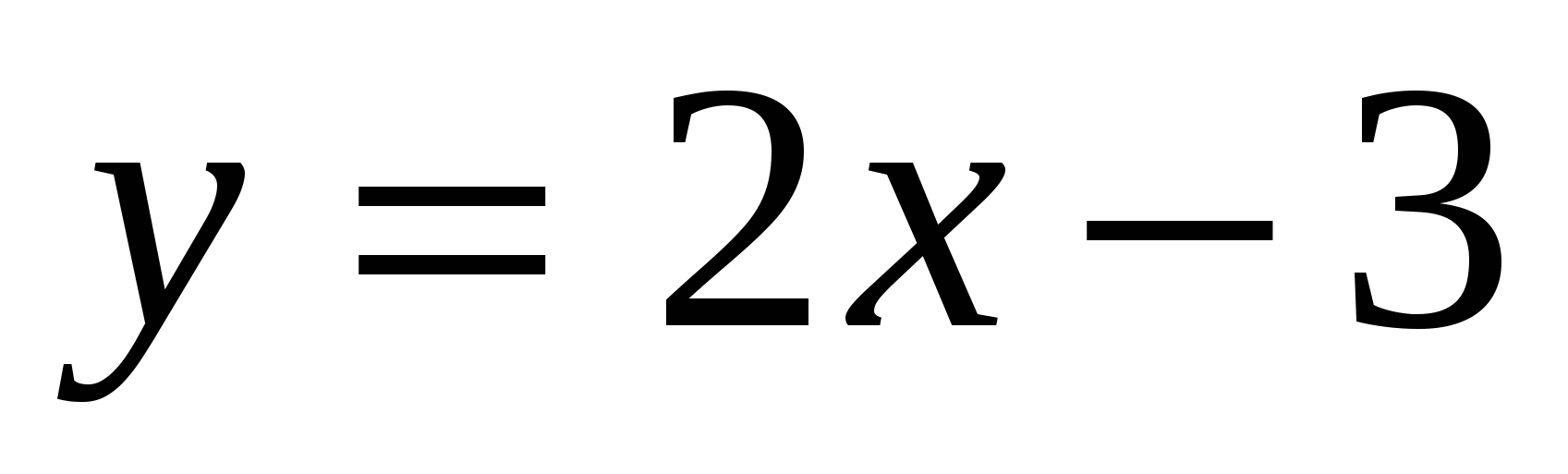 ,
, 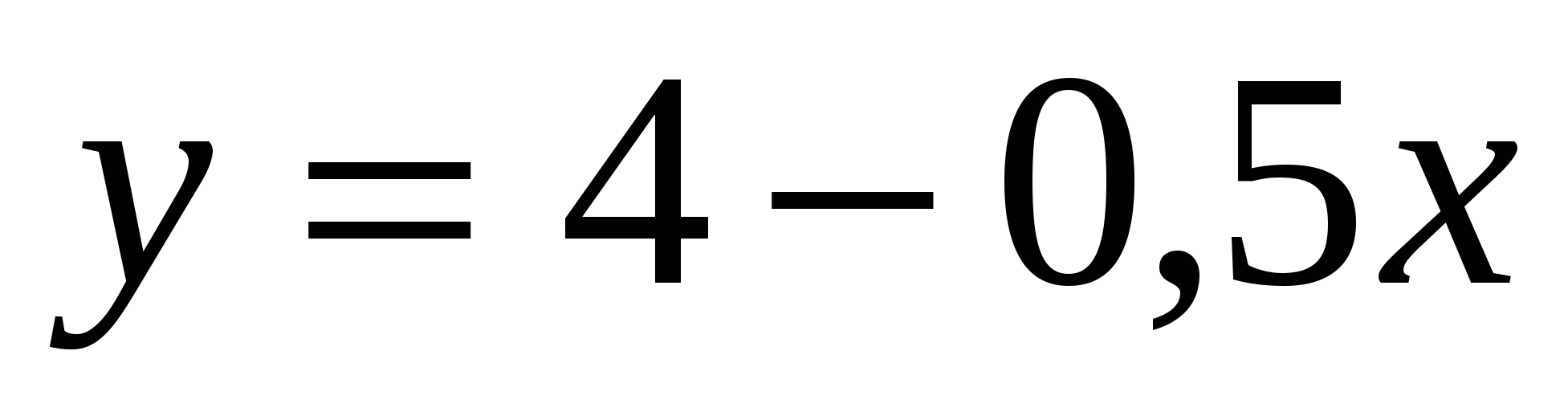 . 2)
. 2) 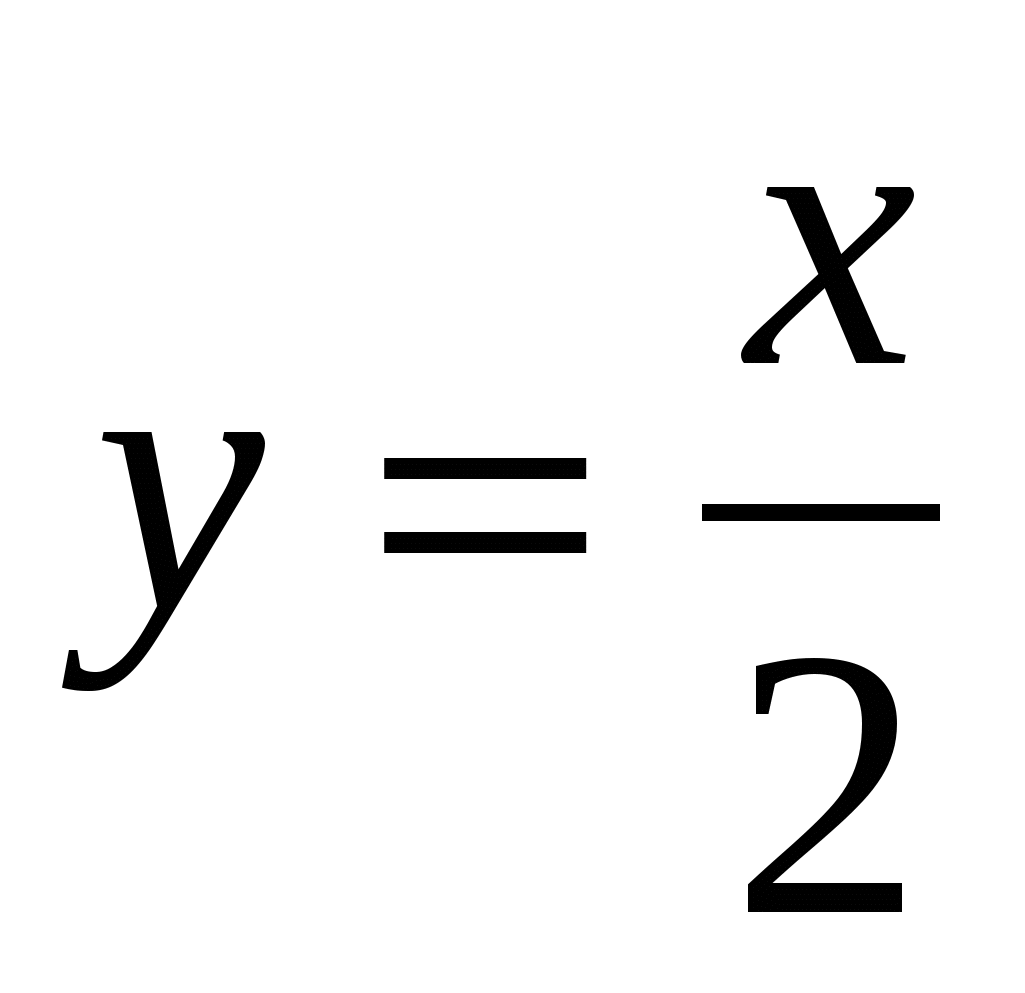 ,
, 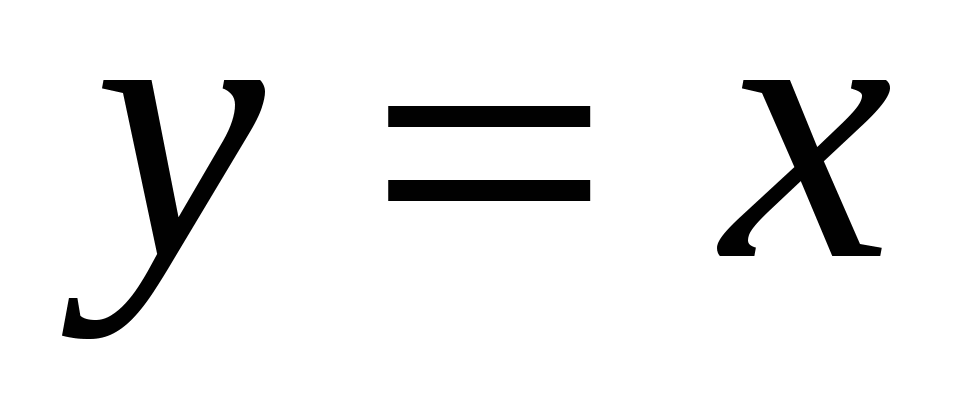 ,
,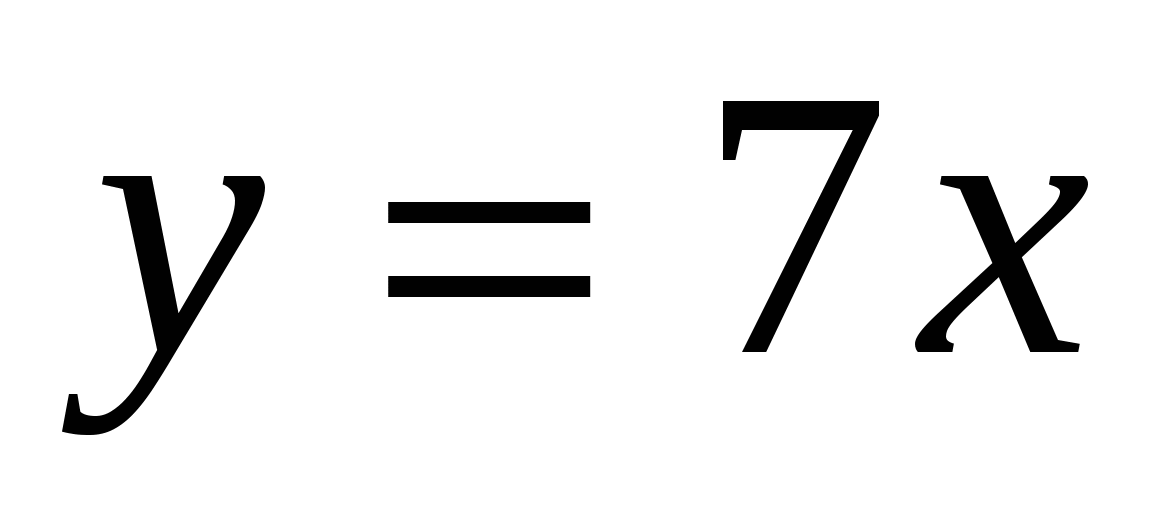
– Как называются функции из первой группы? (Линейные)
– Назовите числа 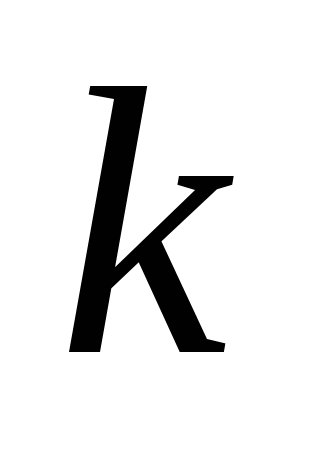 и
и 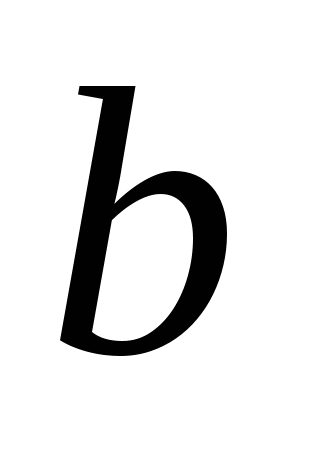 в формулах линейных функций. (
в формулах линейных функций. (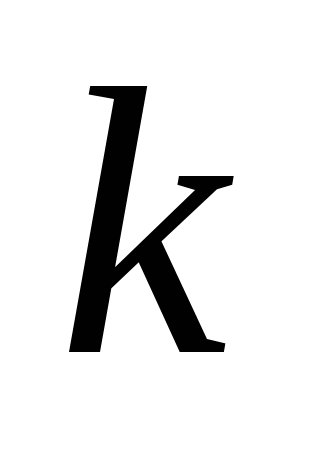 =2,
=2, 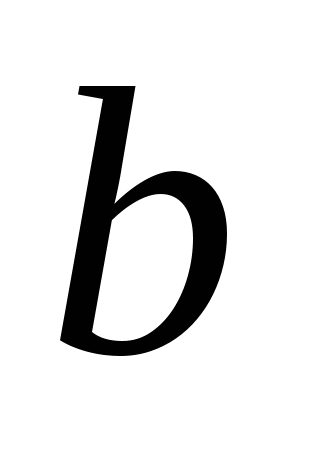 = -3,
= -3, 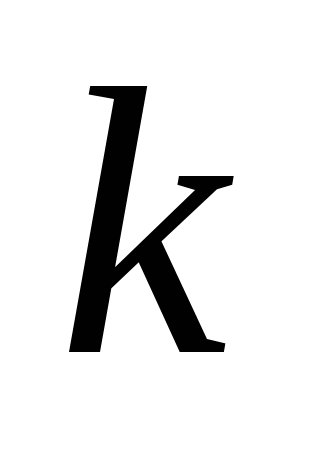 = -0,5,
= -0,5, 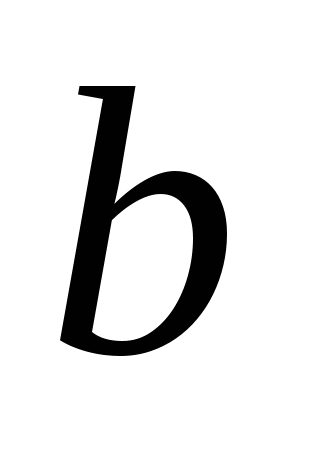 =4)
=4)
– Скольких точек достаточно для построения графиков этих функций? ( Двух)
– Как называются функции из второй группы? (Такие функции называются прямой пропорциональностью.)
– Укажите коэффициент 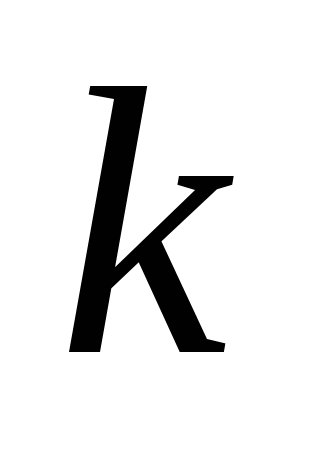 в записях формул данных функций. (
в записях формул данных функций. (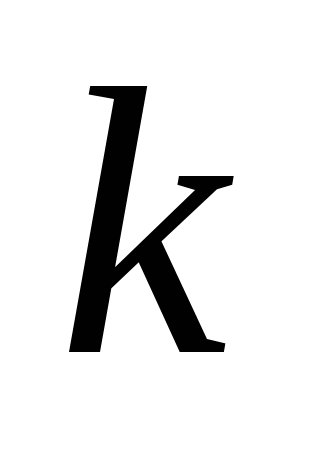 =
=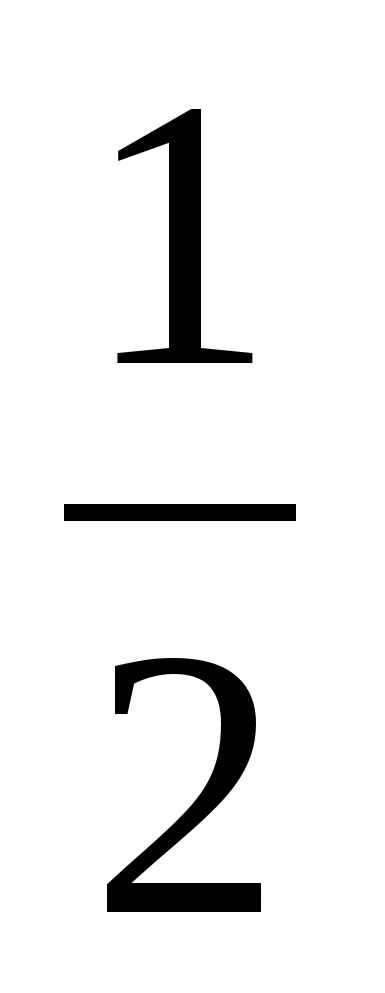 ,
, 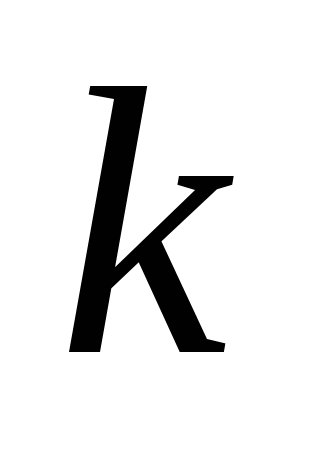 =1,
=1, 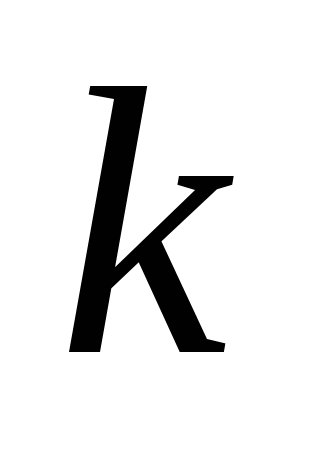 =7,)
=7,)
– Чему равно 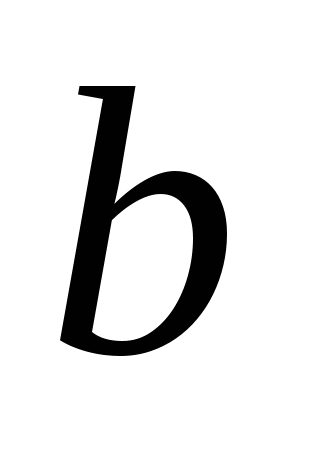 в записях всех данных формул? (
в записях всех данных формул? (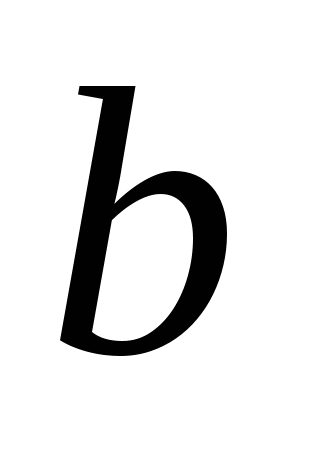 =0.)
=0.)
– Сколько точек нужно найти для построения графиков этих функций?( Графики всех данных функций проходят через точку (0; 0), поэтому для построения графиков этих функций достаточно найти координаты одной точки.)
– Какие ещё выделили группы?( 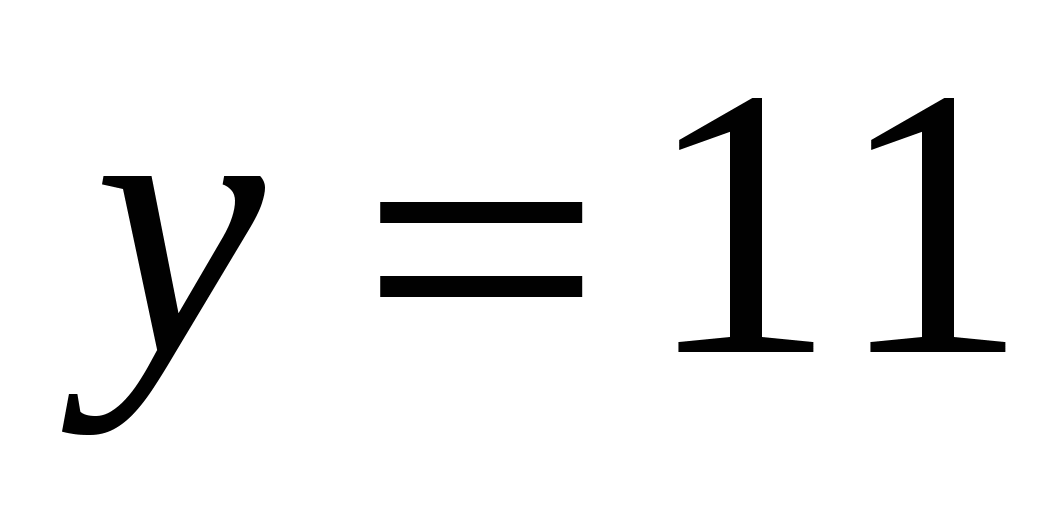 ;
; 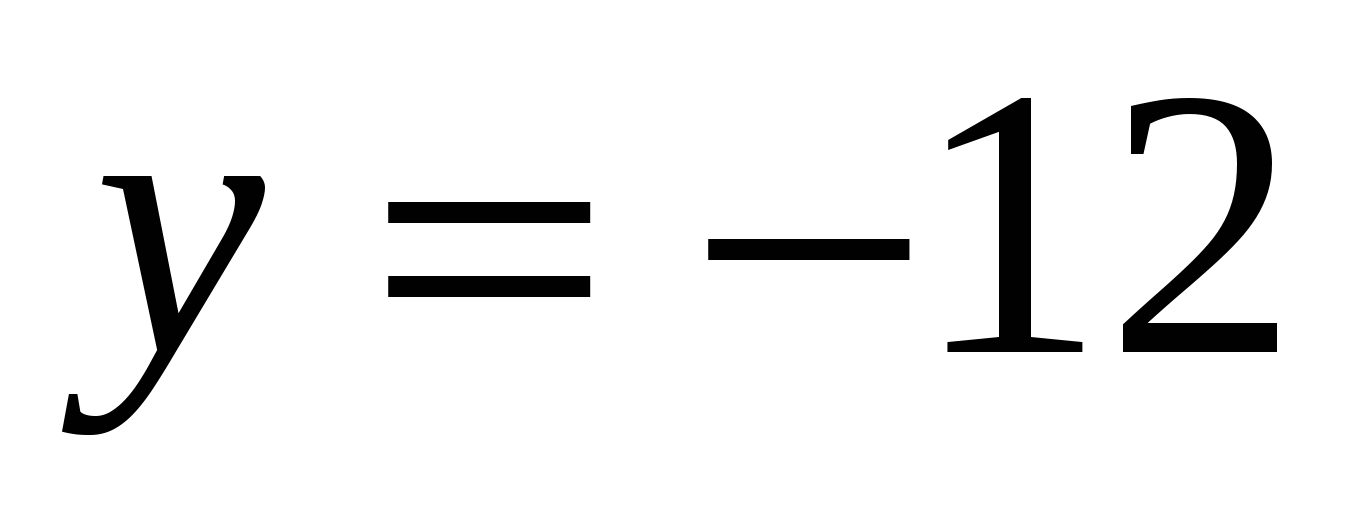 .)
.)
– Как называются такие функции?( Такие функции называются постоянными.)
– Чему равно 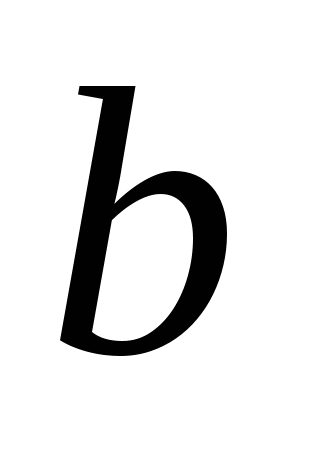 в записях всех данных формул? (
в записях всех данных формул? (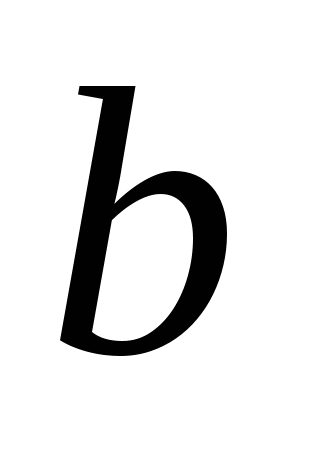 =11,
=11, 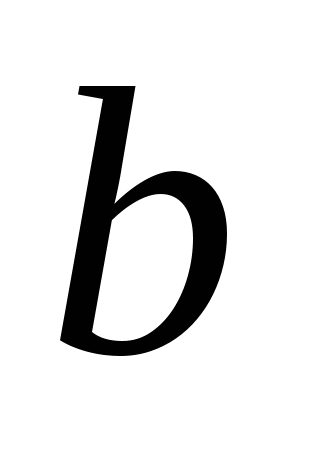 =-12.)
=-12.)
– Чему равен коэффициент 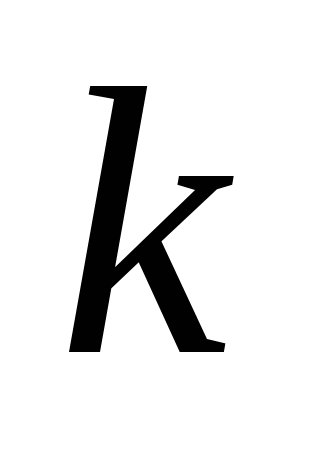 в записях формул данных функций?(
в записях формул данных функций?( 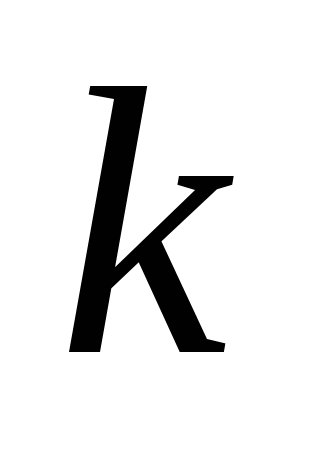 =0).
=0).
– Скольких точек достаточно для построения графиков этих функций? (Двух точек.)
–Чему будет равна ордината каждой из точек, принадлежащих первому графику? (Так как любому значению х соответствует одно и тоже значение у, то ордината каждой из точек будет равна 11.)
–Чему будет равна ордината каждой из точек, принадлежащих второму графику? (Так как любому значению х соответствует одно и тоже значение у, то ордината каждой из точек будет равна -12.)
– Как могут располагаться две произвольные прямые на плоскости? (Две прямые могут быть параллельными, могут пересекаться и совпадать.)
3. Введение в тему. Постановка учебных задач.
Цель: Обеспечить целеполагание.
Мы с вами знаем, что графиком линейной функции является прямая, поэтому графики двух линейных функций тоже могут быть параллельными, могут пересекаться и совпадать.
А теперь выясним, что нового должны узнать на уроке, что выяснить, чему научиться? (Расположение графиков линейных функций.)
На основе предыдущих рассуждений попытайтесь самостоятельно сформулировать тему урока. (Взаимное расположение графиков линейных функций.)
Учитель корректирует ответы учащихся.
Тема урока: Взаимное расположение графиков линейных функций. Открывается слайд №3.
Выясним, что должны узнать на уроке.
Попытайтесь самостоятельно поставить цель, которую вы хотите достичь.
( Возможные ответы:
– Должны рассмотреть параллельность, пересечение и совпадение графиков линейных функций;
– Графики, каких линейных функций параллельны, пересекаются, совпадают;
– От чего зависит параллельность, пересечение, совпадение графиков линейных функций;
– В каком случае графики двух линейных функций параллельны, в каком случае пересекаются, в каком случае совпадают.)
4. Ознакомление с новым материалом.
Цель: Создать условия для введения нового материала.
-А сейчас вы выполните графическую работу, которая поможет вам ответить на поставленные вопросы.
Учитель обращает внимание учащихся на индивидуальные рабочие листы.
Задание№1.
В одной системе координат постройте графики функций:
1. , 2.
, 2. 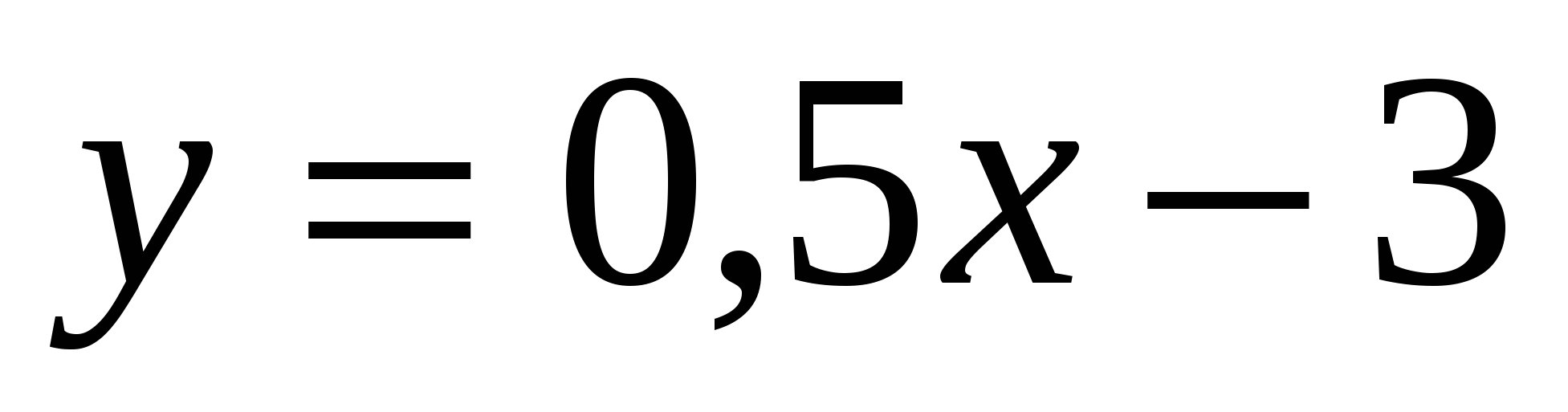 3*.
3*. 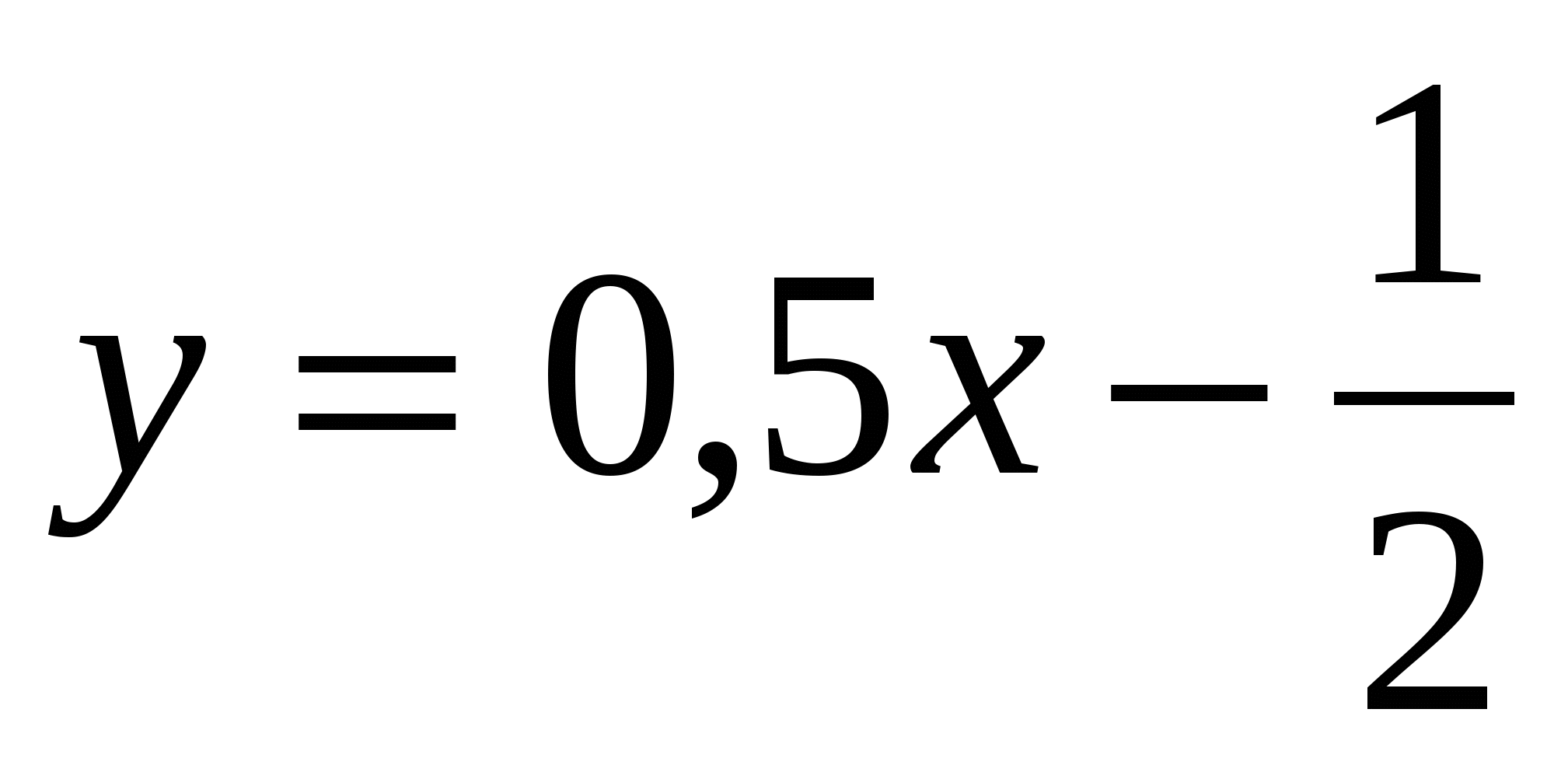 .
.
Задание№2.
В одной системе координат постройте графики
функций:
1.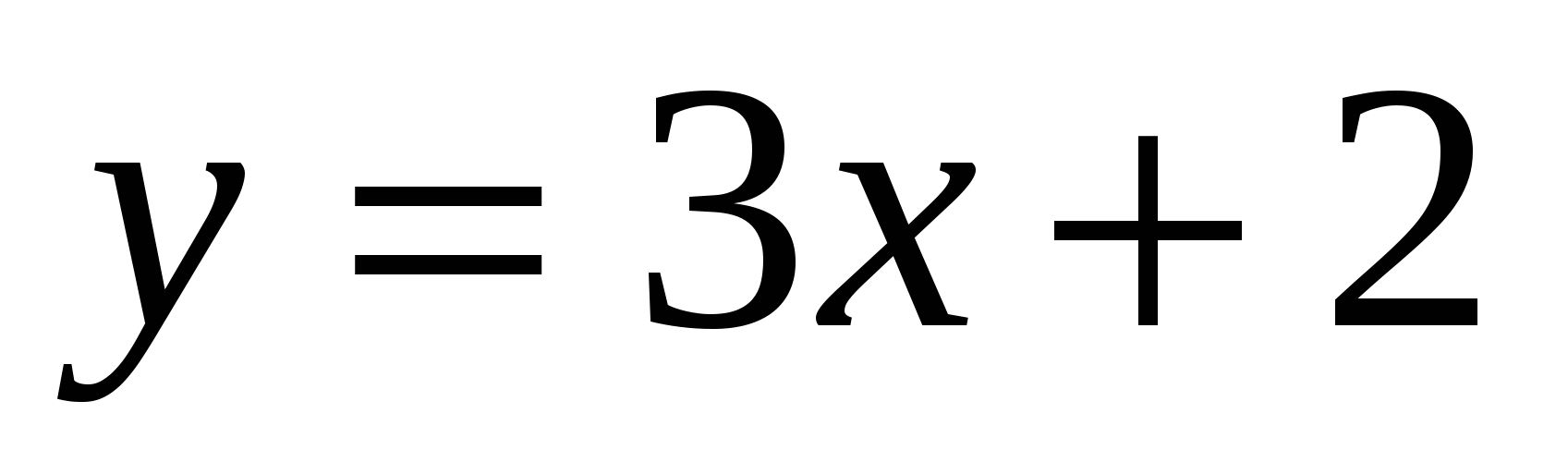 , 2.
, 2. 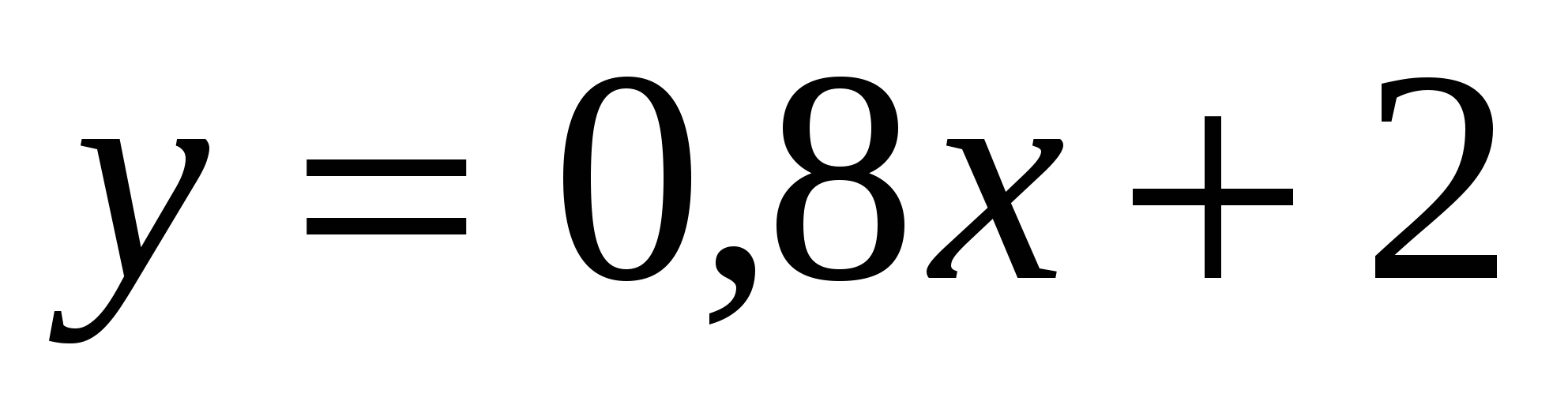 , 3*.
, 3*.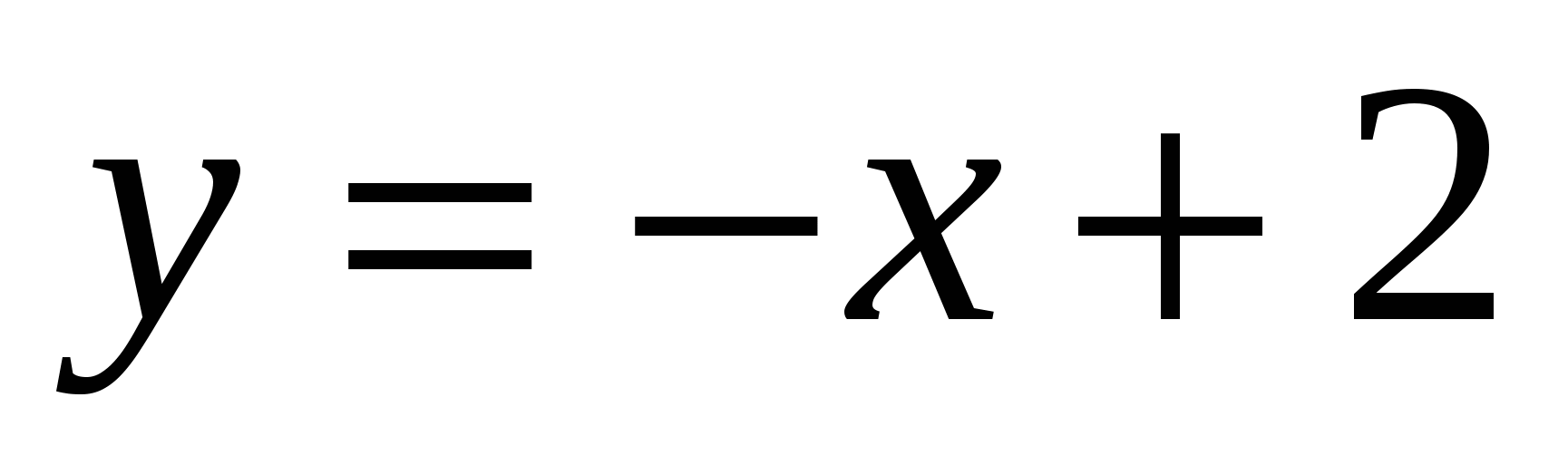 .
.
Задание№3.
В одной системе координат постройте графики функций:
1. 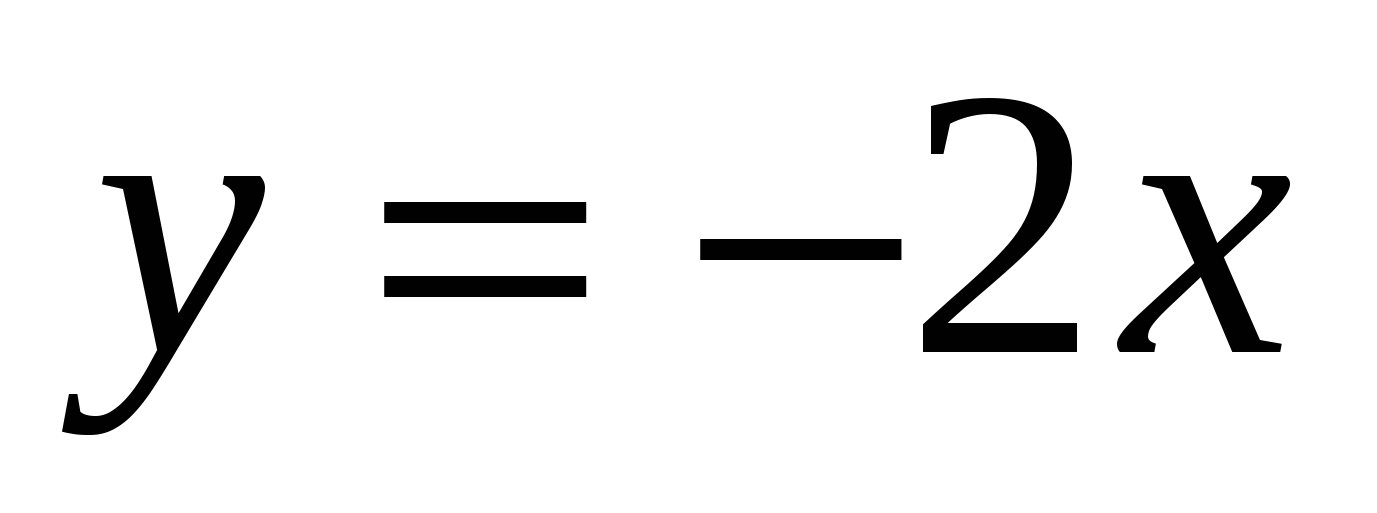 , 2.
, 2. 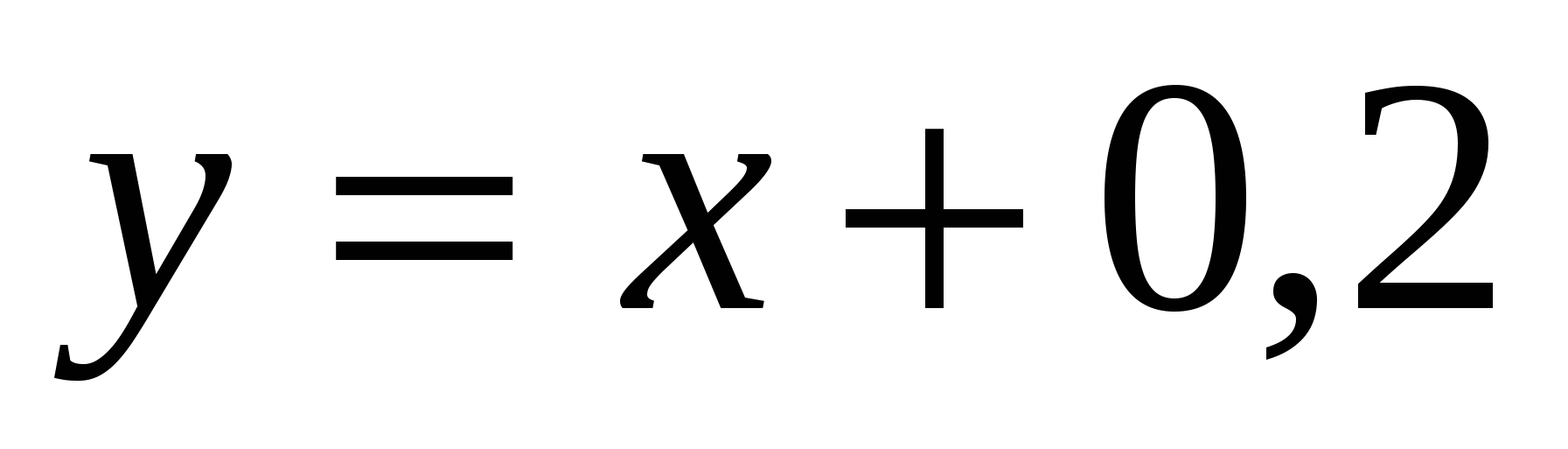 , 3*.
, 3*.
Учитель знакомит учащихся с заданиями:
– Построение графика функции под цифрой 3* выполняете, если уже построено по два графика в каждой группе заданий.
– В итоге выполнения заданий у вас в тетради должно быть изображены три системы координат, в каждой из которых обязательно по два графика. У сильных учащихся в тетрадях возможно – по три графика.
Учитель даёт возможность каждому учащемуся самостоятельно определиться с формой работы.
Те учащиеся, которые уверены в своих силах и могут самостоятельно построить все графики садятся на левый ряд и работают самостоятельно. Учитель контролирует их деятельность.
Остальные, которые не уверены в своих силах, садятся на правый ряд и выполняют построение, обращаясь за помощью к учителю.
После выполнения заданий в тетрадях изображены три системы координат, в каждой из которых по два графика, а у сильных учащихся в тетрадях возможно – по три графика. После выполнения построения открывают слайд с построенным заданием №1.
Открывается слайд №4.
– Обратите внимание на слайд.
–Посмотрите на формулы, задающие графики этих функций, что вы заметили? (Коэффициенты при 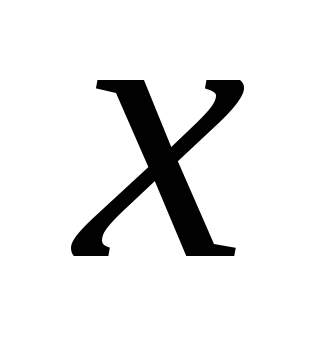 одинаковые.)
одинаковые.)
–Обратите внимание на то, как расположены графики этих функций?( Графики данных функций параллельны.)
– Какой вывод можно сделать, сопоставив запись формул, задающих функции и взаимное расположение их графиков? Возможные ответы:
– Когда коэффициенты равны, то графики параллельны.
– Графики линейных функций параллельны, если коэффициенты при 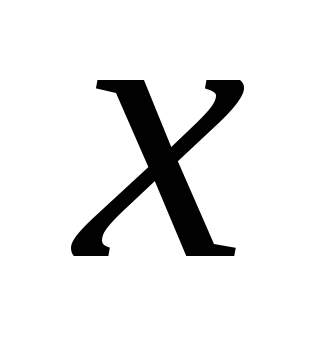 одинаковые.
одинаковые.
- Как графики данных функций располагаются по отношению к оси ох? Возможные ответы:
– Графики пересекают ось.
– Графики данных функций наклонены к оси ох под одним и тем же углом.
- Верно, и этот угол зависит от коэффициента 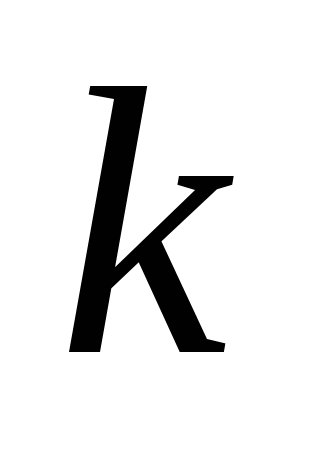 , который называется угловым коэффициентом прямой графика функции
, который называется угловым коэффициентом прямой графика функции 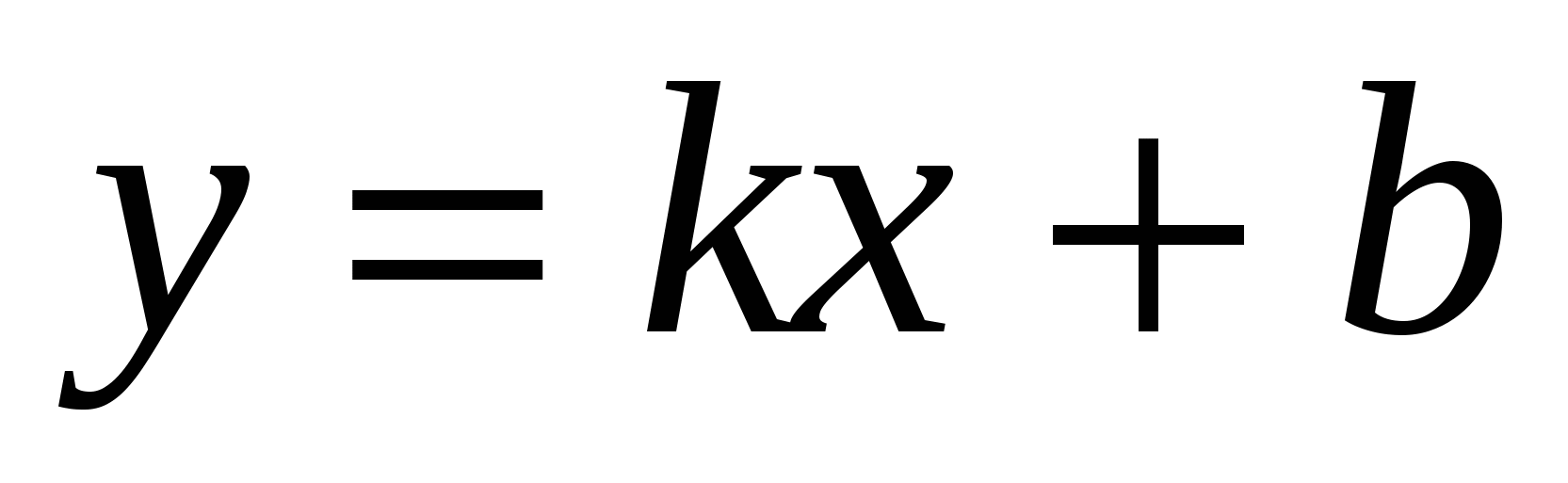 .
.
Отметьте на чертеже углы наклона графиков функций к оси ох.
Открывается слайд №5.
Работаем над заданием №2.
Учитель задаёт аналогичные вопросы, а также обращает внимание на то, в какой точке пересекаются прямые. Возможные ответы:
– Коэффициенты при 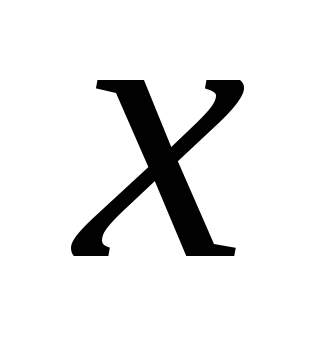 различные, а
различные, а 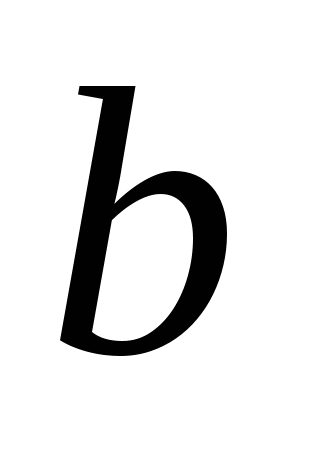 одинаковые.
одинаковые.
– Графики пересекаются.
– Прямые пересекаются в точке (0; 2).
– Графики пересекаются, когда 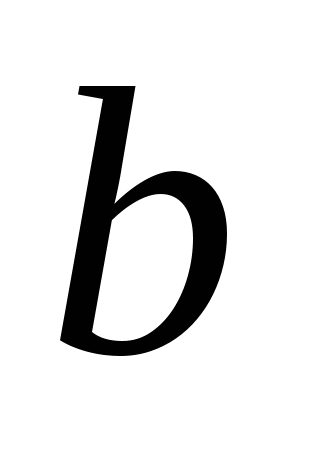 одинаковые.
одинаковые.
Точка пересечения (0; 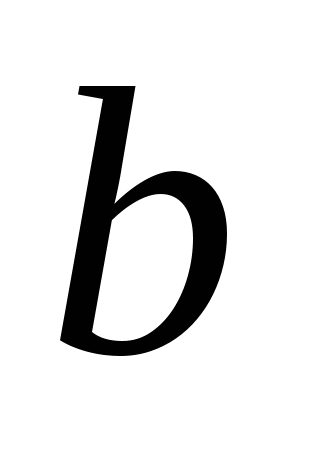 ).
).
– Графики пересекаются, когда коэффициенты при 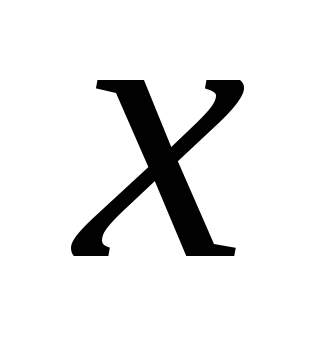 различны.
различны.
Открывается слайд №6.
Работаем над заданием №3.
Учитель задаёт аналогичные вопросы, что и при работе над заданием №1.
– Коэффициенты при 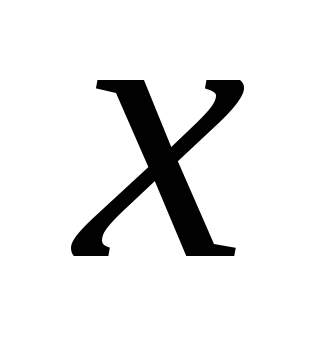 различные и
различные и 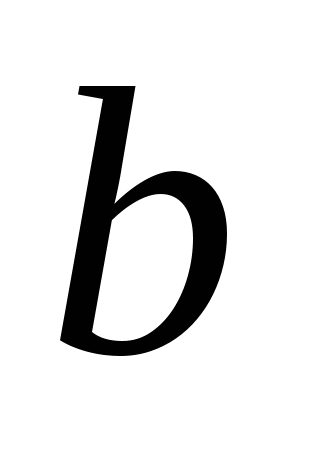 различные.
различные.
– Графики пересекаются.
– Графики пересекаются, когда коэффициенты при 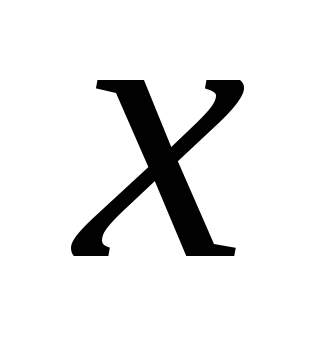 различны.
различны.
– Откройте учебник на странице 65 и проверьте, правильные ли мы с вами сделали выводы.
– Обратите внимание на цели, которые вы поставили в начале урока.
– На какой вопрос осталось ответить? В каком случае графики двух линейных функций совпадают.
–В каком же случае графики двух линейных функций совпадают? –Графики двух линейных функций совпадают, в том случае, если совпадают 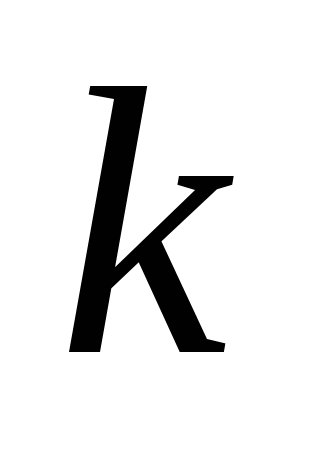 и
и 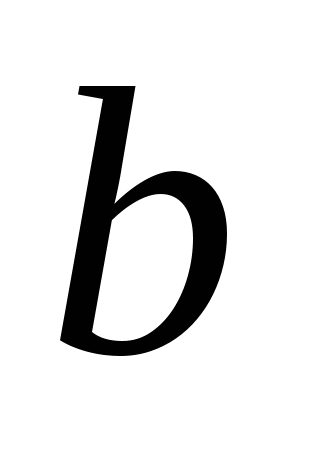 .
.
Запишите выводы в тетрадь.
5. Первичное осмысление и закрепление изученного.
Цель: Создать условия для первичного осмысления и закрепления полученных знаний.
Ученики выполняют задания второй части индивидуальных рабочих листов.
Задание 4. САМОСТОЯТЕЛЬНАЯ РАБОТА учащихся.
Графики каких из данных функций параллельны графику функции у = 0,5 х+1:
у = х + 0,5;. у = 0,5х; у = - 0,5х + 1; у = 8х + 1; у = 0,5х + 8; у = 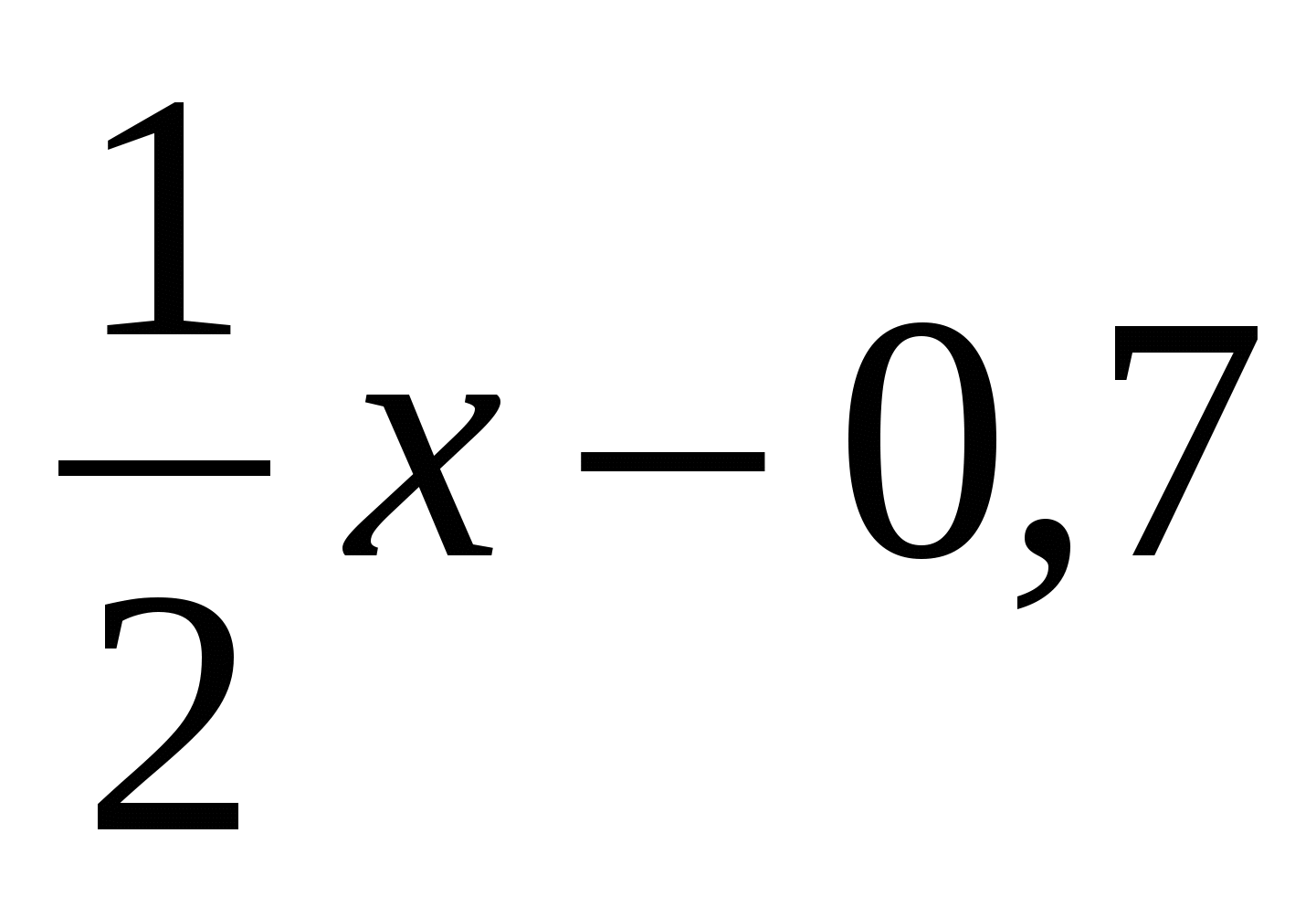 ?
?
а) выпиши формулы, задающие эти функции;
б) Графики каких из данных функций пересекает график функции у = 0,5 х+1? Постройте эти графики.
6. Рефлексия
Цель: Создать условия для формирования навыков самоанализа.
- Что делали на уроке?
- Что нового узнали на уроке?
Сделайте вывод.
Учитель оценивает работу: учитывает правильность, самостоятельность, оригинальность.
7. Домашнее задание.
Цель: Дать инструкцию по выполнению домашнего задания.
П. 15 № 337, 339, 341(а, в)
8. Итог урока.
Цель: Подвести итоги урока, обобщить и систематизировать знания, полученные на уроке.
- Что делали на уроке? Что нового узнали на уроке?Сделайте вывод.
Учитель оценивает работу: учитывает правильность, самостоятельность, оригинальность. Учитель выставляет отметки.