«Методы решения уравнений высших степеней»
( Киселёвские чтения)
Учитель математики Афанасьева Л.А
МКОУ Верхнекарачанская СОШ
Грибановского района, Воронежской области
2015 год
Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека.
Известный немецкий математик Курант писал: «На протяжении двух с лишним тысячелетий обладание некоторыми, не слишком поверхностными, знаниями в области математики входило необходимой составной частью в интеллектуальный инвентарь каждого образованного человека». И среди этих знаний не последнее место принадлежит умению решать уравнения.
Уже в древности люди осознали, как важно научиться решать алгебраические уравнения. Около 4000 лет назад вавилонские ученые владели решением квадратного уравнения и решали системы двух уравнений, из которых одно – второй степени. С помощью уравнений решались разнообразные задачи землемерия, архитектуры и военного дела, к ним сводились многие и разнообразные вопросы практики и естествознания, так как точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными. Уравнение одно из важнейших понятий математики. Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры. И сегодня на уроках математики, начиная с первой ступени обучения, решению уравнений различных видов уделяется большое внимание.
Универсальной формулы для нахождения корней алгебраического уравнения n – ой степени нет. Многим, разумеется, приходила в голову заманчивая мысль найти для любой степени n формулы, которые выражали бы корни уравнения через его коэффициенты, то есть, решали бы уравнение в радикалах. Однако «мрачное средневековье» оказалось как нельзя более мрачным и в отношении обсуждаемой задачи – в течение целых семи столетий требуемых формул никто не нашёл! Только в 16 веке итальянским математикам удалось продвинуться дальше – найти формулы для n=3 и n=4. Одновременно вопросом об общем решении уравнений 3-й степени занимались Сципион Даль Ферро, его ученик Фиори и Тарталья. В 1545 году вышла книга итальянского математика Д Кардано «Великое искусство, или О правилах алгебры», где наряду с другими вопросами алгебры рассматриваются общие способы решения кубических уравнений, а так же метод решения уравнений 4 – й степени, открытый его учеником Л. Феррари. Полное изложение вопросов, связанных с решением уравнений 3-й 4-й степеней, дал Ф. Виет. А в 20-х годах 19 века норвежский математик Н. Абель доказал, что корни уравнений 5-й и более высоких степеней не могут быть выражены через радикалы.
Процесс отыскания решений уравнения заключается обычно в замене уравнения равносильным. Замена уравнения равносильным основана на применении четырёх аксиом:
1. Если равные величины увеличить на одно и то же число, то результаты будут равны.
2. Если из равных величин вычесть одно и то же число, то результаты будут равны.
3. Если равные величины умножить на одно и то же число, то результаты будут равны.
4. Если равные величины разделить на одно и то же число, то результаты будут равны.
Поскольку левая часть уравнения Р(х) = 0 представляет собой многочлен n-й степени, то полезно напомнить следующие утверждения:
Утверждения о корнях многочлена и его делителях:
1. Многочлен n-й степени имеет число корней не превышающее число n, причем корни кратности m встречаются ровно m раз.
2. Многочлен нечетной степени имеет хотя бы один действительный корень.
3. Если α – корень Р(х), то Рn (х) = (х - α)·Qn - 1(x), где Qn - 1(x) – многочлен степени (n – 1).
4. Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.
5. Приведенный многочлен с целыми коэффициентами не может иметь дробных рациональных корней.
6. Для многочлена третьей степени
Р3(х) = ах3 + bx2 + cx + d возможно одно из двух: либо он разлагается в произведение трех двучленов
Р3(x) = а (х - α)(х - β)(х - γ), либо разлагается в произведение двучлена и квадратного трехчлена Р3(x) = а(х - α)(х2 + βх + γ).
7. Любой многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов.
8. Многочлен f (x) делится на многочлен g(х) без остатка, если существует многочлен q(x), что f(x) = g(x)·q(x). Для деления многочленов применяется правило «деления уголком».
9. Для делимости многочлена P(x) на двучлен (x – c) необходимо и достаточно, чтобы с было корнем P(x) (Следствие теоремы Безу).
10. Теорема Виета: Если х1, х2, …, хn – действительные корни многочлена
Р(х) = а0хn + а1хn - 1 + … + аn, то имеют место следующие равенства:
х1 + х2 + … + хn = -а1/а0,
х1 · х2 + х1 · х3 + … + хn - 1 · хn = a2/а0,
х1 · х2 · х3 + … + хn - 2 · хn - 1 · хn = -a3/а0,
х1 · х2 · х3 · хn = (-1)n an/а0.
Решение примеров
Пример 1. Найти остаток от деления Р(х) = х3 + 2/3 x2 – 1/9 на (х – 1/3).
Решение. По следствию из теоремы Безу: «Остаток от деления многочлена на двучлен (х - с) равен значению многочлена от с». Найдем Р(1/3) = 0. Следовательно, остаток равен 0 и число 1/3 – корень многочлена.
Ответ: R = 0.
Пример 2. Разделить «уголком» 2х3 + 3x2 – 2х + 3 на (х + 2). Найти остаток и неполное частное.
Решение:
2х3 + 3x2 – 2х + 3| х + 2
2х3 + 4x2 2x2 – x
-x2 – 2x
-x2 – 2x
3
Ответ: R = 3; частное: 2х2 – х.
Основные методы решения уравнений высших степеней
1. Введение новой переменной
Метод введения новой переменной заключается в том, что для решения уравнения f(x) = 0 вводят новую переменную (подстановку) t = xn или t = g(х) и выражают f(x) через t, получая новое уравнение r(t). Решая затем уравнение r(t), находят корни: (t1, t2, …, tn). После этого получают совокупность n уравнений q(x) = t1, q(x) = t2, … , q(x) = tn, из которых находят корни исходного уравнения.
Пример ; (х2 + х + 1)2 – 3х2 - 3x – 1 = 0.
Решение: (х2 + х + 1)2 – 3х2 - 3x – 1 = 0.
(х2 + х + 1)2 – 3(х2 + x + 1) + 3 – 1 = 0.
Замена (х2 + х + 1) = t.
t2 – 3t + 2 = 0.
t1 = 2, t2 = 1. Обратная замена:
х2 + х + 1 = 2 или х2 + х + 1 = 1;
х2 + х - 1 = 0 или х2 + х = 0;
Из первого уравнения: х1, 2 = (-1 ± √5)/2, из второго: 0 и -1.
Метод введения новой переменной находит применение при решении возвратных уравнений, то есть уравнений вида а0хn+ а1хn – 1 + .. + а n – 1х + аn=0, в котором коэффициенты членов уравнения, одинаково отстоящих от начала и конца, равны.
2. Разложение на множители методом группировки и формул сокращенного умножения
Основа данного метода заключается в группировке слагаемых таким образом, чтобы каждая группа содержала общий множитель. Для этого иногда приходится применять некоторые искусственные приемы.
Пример: х4 - 3x2 + 4х – 3 = 0.
Решение. Представим - 3x2 = -2x2 – x2 и сгруппируем:
(х4 - 2x2) – (x2 - 4х + 3) = 0.
(х4 - 2x2 +1 – 1) – (x2 - 4х + 3 + 1 – 1) = 0.
(х2 – 1)2 – 1 – (x – 2)2 + 1 = 0.
(х2 – 1)2 – (x – 2)2 = 0.
(х2 – 1 – х + 2)(х2 – 1 + х - 2) = 0.
(х2 – х + 1)(х2 + х - 3) = 0.
х2 – х + 1 = 0 или х2 + х - 3 = 0.
В первом уравнении нет корней, из второго: х1, 2 = (-1 ± √13)/2.
3. Разложение на множители методом неопределенных коэффициентов
Суть метода состоит в том, что исходный многочлен раскладывается на множители с неизвестными коэффициентами. Используя свойство, что многочлены равны, если равны их коэффициенты при одинаковых степенях, находят неизвестные коэффициенты разложения.
Пример: х3 + 4x2 + 5х + 2 = 0.
Решение. Многочлен 3-й степени можно разложить в произведение линейного и квадратного множителей.
х3 + 4x2 + 5х + 2 = (х - а)(x2 + bх + c),
х3 + 4x2 + 5х + 2 = х3 +bx2 + cх - ax2 - abх - ac,
х3 + 4x2 + 5х + 2 = х3 + (b – a)x2 + (c – ab)х – ac.
Решив систему: 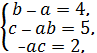
получим 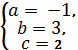
х3 + 4x2 + 5х + 2 = (х + 1)(x2 + 3х + 2).
Корни уравнения (х + 1)(x2 + 3х + 2) = 0 находятся легко.
Ответ: -1; -2.
4. Метод подбора корня по старшему и свободному коэффициенту
Метод опирается на применение теорем:
1) Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.
2) Для того, чтобы несократимая дробь p/q (p – целое, q - натуральное) была корнем уравнения с целыми коэффициентами, необходимо, чтобы число p было целым делителем свободного члена а0, а q – натуральным делителем старшего коэффициента.
Пример: 6х3 + 7x2 - 9х + 2 = 0.
Решение:
2 : p = ±1, ±2
6 : q = 1, 2, 3, 6.
Следовательно, p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.
Найдя один корень, например – 2, другие корни найдем, используя деление уголком, метод неопределенных коэффициентов или схему Горнера.
Ответ: -2; 1/2; 1/3.
5. Графический метод.
Данный метод состоит в построении графиков и использовании свойств функций.
Пример: х5 + х – 2 = 0
Представим уравнение в виде х5 = - х + 2. Функция у = х5 является возрастающей, а функция у = - х + 2 - убывающей. Значит, уравнение х5 + х – 2 = 0 имеет единственный корень -1.
6.Умножение уравнения на функцию.
Иногда решение алгебраического уравнения существенно облегчается, если умножить обе его части на некоторую функцию – многочлен от неизвестной. При этом надо помнить, что возможно появление лишних корней – корней многочлена, на который умножили уравнение. Поэтому надо либо умножать на многочлен, не имеющий корней, и получить равносильное уравнение, либо умножать на многочлен, имеющий корни, и тогда каждый из таких корней надо обязательно подставить в исходное уравнение и установить, является ли это число его корнем.
Пример. Решить уравнение:
X8 – X6 + X4 – X 2 + 1 = 0. (1)
Решение: Умножив обе части уравнения на многочлен Х2 + 1, не имеющий корней, получим уравнение:
(Х2 +1) (Х8 – Х 6 + Х4 – Х 2 + 1) = 0 (2)равносильное уравнению (1). Уравнение (2) можно записать в виде:
Х10 + 1= 0 (3)Ясно, что уравнение (3) не имеет действительных корней, поэтому уравнение (1) их не имеет.
Ответ: нет решений.
Кроме названных методов решения уравнений высших степеней существуют и другие. Например, выделение полного квадрата, схема Горнера, представление дроби в виде двух дробей. Из общих методов решения уравнений высших степеней, которые встречаются чаще всего, используют: метод разложения левой части уравнения на множители;
метод замены переменной (метод введения новой переменной); графический способ. С этими методами мы знакомим учащихся 9 класса при изучении темы «Целое уравнение и его корни». В учебнике Алгебра 9 (авторы Макарычев Ю.Н., Миндюк Н.Г и др) последних годов издания достаточно подробно рассматриваются основные методы решения уравнений высших степеней. Кроме этого в разделе «Для тех, кто хочет знать больше», на мой взгляд, доступно излагается материал о применении теорем о корне многочлена и целых корнях целого уравнения при решении уравнений высших степеней. Хорошо подготовленные ученики с интересом изучают этот материал, а затем представляют одноклассникам решённые уравнения.
Практически всё, что окружает нас, связано в той или иной мере с математикой. А достижения в физике, технике, информационных технологиях только подтверждают это. И что очень важно – решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.