Урок алгебры в 7 классе
на тему "Линейная функция и ее график"
Цели:
применение возможностей программы GeoGebra и интерактивной
творческой среды для создания математических моделей;
изучить определение линейной функции;
совершенствовать навыки построения прямых по координатам точек ;
закрепить понятие углового коэффициента k к прямой;
составлять уравнения прямой по заданным k и b.
Технология применение средств ИКТ в предметном обучении основывается на:
Использование программы GeoGebra деятельности учителя, управляющим этой технологией;
Повышении мотивации и активности обучающихся, вызываемой интерактивными возможностями компьютерной программы GeoGebra.
В содержании конспекта урока используются ИКТ работа с программой GeoGebra, проблемное обучение, здоровьесберегающая технология (физминутка), отражен дифференцированный подход.
Ход урока
1.Актуализация знаний учащихся.
Фронтальный опрос:
Какую функцию называют прямой пропорциональностью?
Что является графиком прямой пропорциональности?
От чего зависит расположение графика прямой пропорциональности?
Проверка д/з:
№ 303 Принадлежат ли графику функции y= - 0,5х точки С (2;-1), Д (4;-20).
Решение: Подставим абсциссу и ординату точки С в функцию , -1= - 0,5 ∙ 2
-1= - 1 - верно
Точка С Є графику функции у= - 0,5 х.
Подставим абсциссу и ординату точки D в функцию, -20 = - 0,5 ∙ 4
- 20 = - 2 - неверно
Точка D не Є графику функции у= - 0,5 х
№ 305
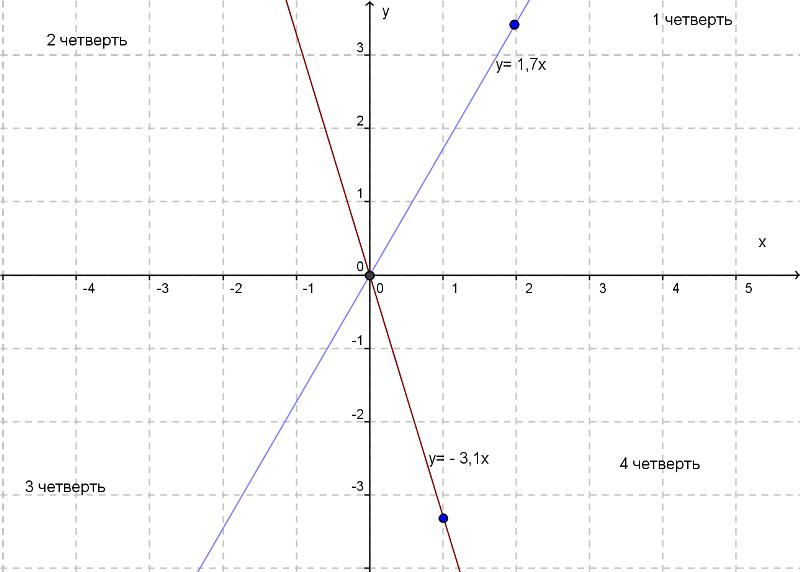
Итог д/р
График функции у= 1,7х , расположен в 1и 3 координатных четвертях, т.к. 1,7 >0.
График функции у= - 3,1х, расположен во 2и 4 координатных четвертях , т.к. – 3,1 < 0.
2. Изучение нового материала.
Линейной функцией называется функция, которую можно задать формулой вида y=kx+b, где x – независимая переменная, k и b – некоторые числа.
Графиком линейной функции является прямая.
Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки на координатной плоскости и провести через них прямую.
Расположение графика функции y=kx+b на координатной плоскости зависит от коэффициентов k и b
Прямая пропорциональность является частным случаем линейной функции при b = 0.
Возьмем графики функции y = 0,5x и у = 0,5х + 2.
Составим таблицы соответственных значений переменных х и у для некоторых значений аргумента х:
у= 0,5х
х
0
2
у
0
1
у= 0,5х + 2
х
0
2
у
2
3
Отметим в координатной плоскости точки, координаты которых помещены в таблице.
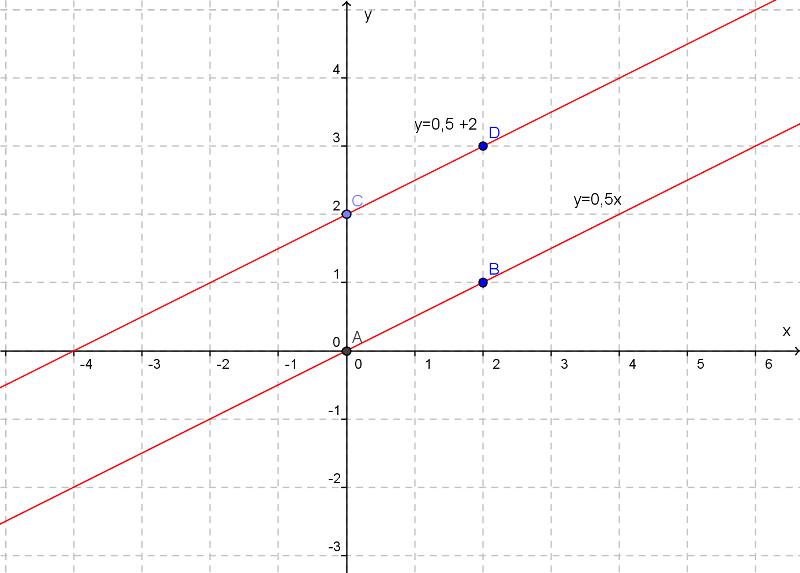
Следовательно
Если график функции у = 0,5x сдвинуть на 2 единицы вверх, то каждая точка графика функции у = 0,5х перейдет в точку графика функции у = 0,5х + 2. При этом каждая ордината точки увеличилась на 2.
График функции y=kx+b, где k 0, есть прямая, параллельная прямой y=kx.
0, есть прямая, параллельная прямой y=kx.
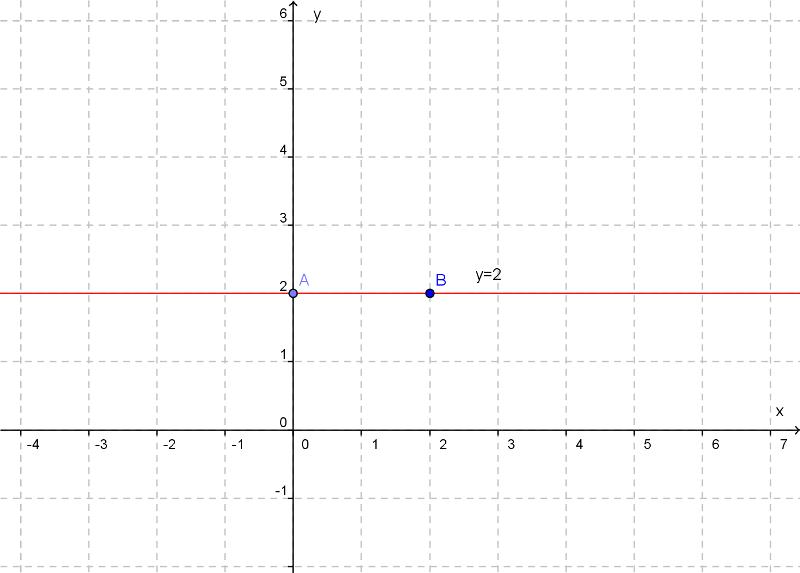
Если k=0, то формула y=kx+b принимает вид y = b. Графиком функции y = kx + b является прямая, параллельная оси х при b 0 или сама ось х при b = 0.
0 или сама ось х при b = 0.
Если k=0, b=2, прямая проходит через точку (0;2)
3. Закрепление изученного материала.
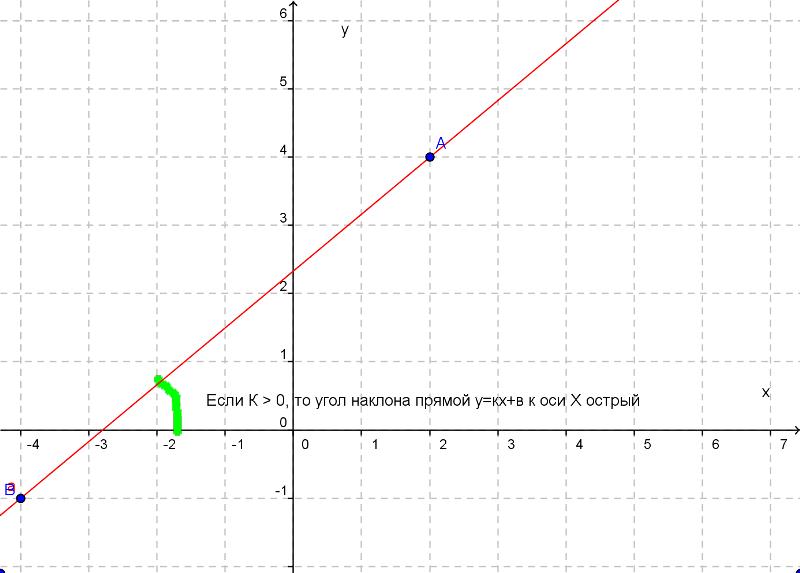
Число k называется угловым коэффициентом прямой –
графика функции у = kx + b.
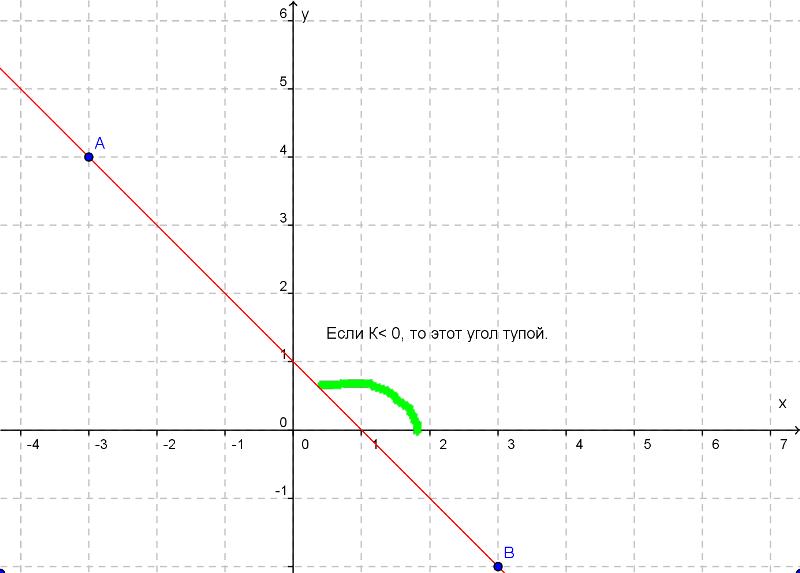
Если k>0, то угол наклона прямой у=kx+b к оси х острый;
если k<0, то этот угол тупой.
4. Физминутка
Ребята на минутку закройте все глаза, расслабьтесь, выпрямите спинки
“Расположение графика линейной функции” (раздаточный материал, рефлексия)
k
b
y = kx + b
Схематический вид графика
k
b
y = kx + b
Схематический вид графика
2
3
-3
2
2
0
-3
0
5
3
-4
5
4
-2
-2
-2
0
3
0
-5
Выводы.
Если k>0, то угол наклона, образованный графиком линейной функции, с положительным направлением оси Ох ________________________________________ .
Если k<0, то угол наклона, образованный графиком линейной функции, с положительным направлением оси Ох ________________________________________
Если k = 0, то график линейной функции расположен _____________________ оси Ох.
Если b > 0, то график функции y = kx + b получается сдвигом графика функции y = kx на ______ единиц ______ (вверх/вниз) вдоль оси ______.
Если b < 0, то график функции y = kx + b получается сдвигом графика функции y = kx на ______ единиц ______ (вверх/вниз) вдоль оси ___________.
Таким образом, график функции y = kx + b получается сдвигом графика функции y = kx на ______ единиц вдоль оси ___________.
Является ли линейной функция, заданная формулой:
№ 316 (устно)
а) у = 2х – 3 - да; 3)  - да;
- да;
2) ; у = х2 – 3 - нет;
5. Домашнее задание.
П.16, стр. 70, № 320, № 326(а,б)