Муниципальное образовательное учреждение
Лемешкинская средняя общеобразовательная школа
Руднянского муниципального района Волгоградской области.
Урок алгебры в 9 классе на тему:
«Решение неравенств второй степени с одной переменной»
Автор: Бодылева О.М., учитель информатики, математики.
2010 – 2011 уч. год.
Урок алгебры в 9 классе на тему:
«Решение неравенств второй степени с одной переменной»
Тип урока: урок изучения нового материала, проблемный.
Цели:
- восстановить знания о квадратной функции, познакомиться с методом решения неравенства
ax2+bx+c>0 на основе свойств квадратичной функции;
- обучение сотрудничеству, культуре общения «никогда не берись за последующее, не усвоив
предыдущее» академик И.П. Павлов;
- умение выделять главное, анализировать, делать выводы.
Ход урока.
Ι. Организационный момент.
Тема сегодняшнего урока «Решение неравенств второй степени с одной переменной». Исходя из темы урока, очевидно, сегодня предстоит знакомство с решением неравенств второй степени, использующих свойства квадратичной функции.
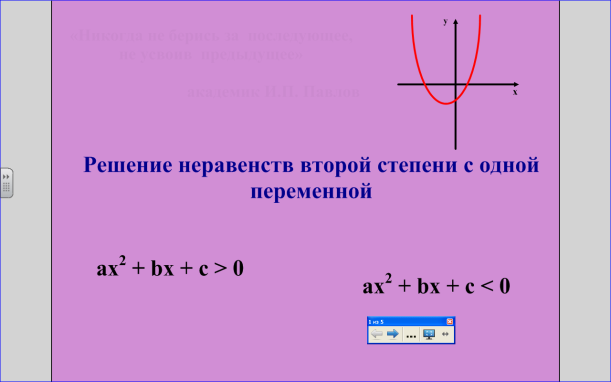

Рис.2
Рис.1
ΙΙ. Актуализация знаний.
Как связаны эти понятия? Как бы вы предложили исследовать связь между ними? На какие вопросы стали отвечать в первую очередь?
Прежде, чем начать изучение, я хочу обратиться к словам академика И.П.Павлова «Никогда не берись за последующее, не усвоив предыдущее». Для этого проведём разминку по изученному материалу.
1 задание: Соотнесите условие и график квадратичной функции. ( рис. 3)
2 задание: Назовите промежутки знакопостоянства функции, если её график расположен
следующим образом. ( рис. 4)
3 задание: Задание с секретом. Установите соответствие между функцией и её графиком.( рис. 5)
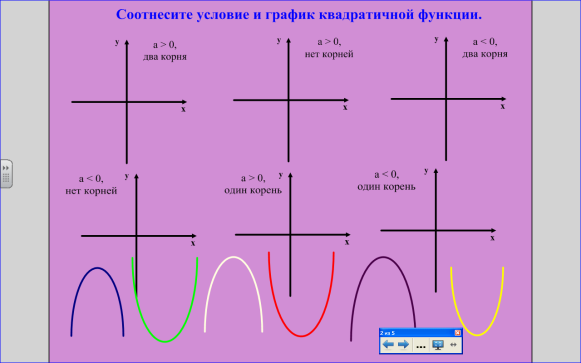
Рис.4
Рис.5
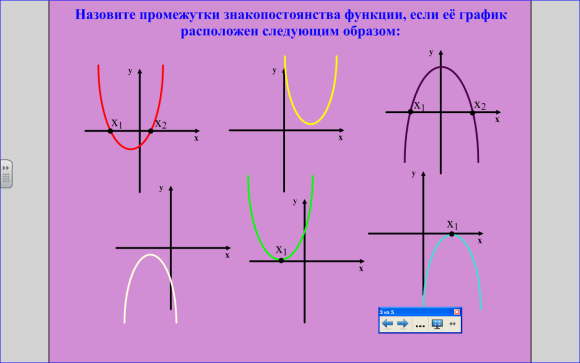
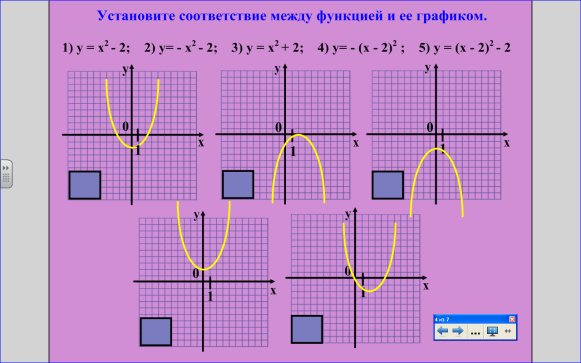
Рис.3
Ответ: ФОКУС – точка на оси параболы, луч света, помещенный при помощи зеркала в эту точку, отражается параллельно оси симметрии. Используется в приборостроении, отражатели (телескоп, автомобильные фары, прожектор, карманный фонарик). Из биографии Архимеда (сжег неприятельский флот).
ΙΙΙ. Изучение нового материала.
Вот так, используя промежутки знакопостоянства квадратичной функции, решают неравенства вида ax2 + bx + c > 0 , ax2 + bx + c < 0, которые называются неравенствами второй степени с одной переменной. ( рис. 6)

Рис.6
Вернемся к поставленным вопросам. Какие появились идеи? Какой способ решения неравенств будем использовать? ( Графический ).
Кто может сформулировать алгоритм решения неравенств второй степени, основанный на свойствах квадратичной функции.
Рассмотрим пример. После разбора примера попробуем вместе сделать некоторые выводы и зафиксируем их в тетрадях. Вам предстоит решить неравенство x2 – x – 30 < 0. ( рис. 7)
Рис.7
Какая информация о квадратичной функции y= x2 – x – 30 может оказаться при этом полезной:
знак коэффициента;
знак D квадратного трёхчлена;
направление ветвей параболы y= x2 – x – 30;
пересечение параболы с осями координат;
координаты вершины параболы;
примерное расположение параболы?
Обязательно ли для решения строить график соответствующей квадратичной функции? Если да, то с какой точностью выполнять построение.
Задание: Проанализируйте решение неравенства x2 – x – 30 < 0. ( рис. 8)
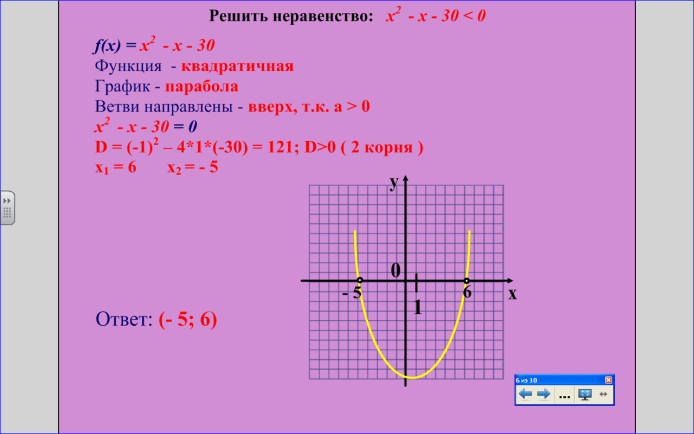
Рис.8
Из каких шагов состоит решение?
Какой вывод вы смогли сделать?
Попробуйте, опираясь на предложенное решение, составить алгоритм решения неравенств второй степени. ( рис. 9)

Рис.9
ΙV. Физминутка.
V. Применение знаний, формирование умений и навыков.
( рис. 10, 11)
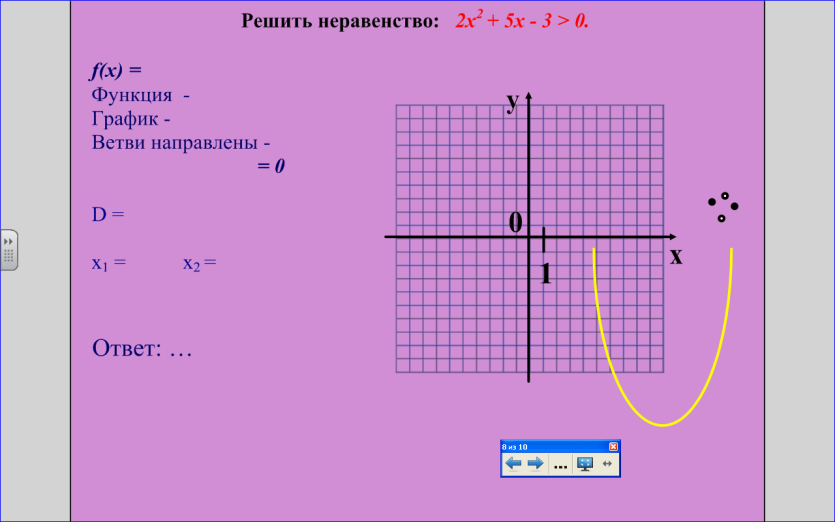
Рис.10
Рис.11
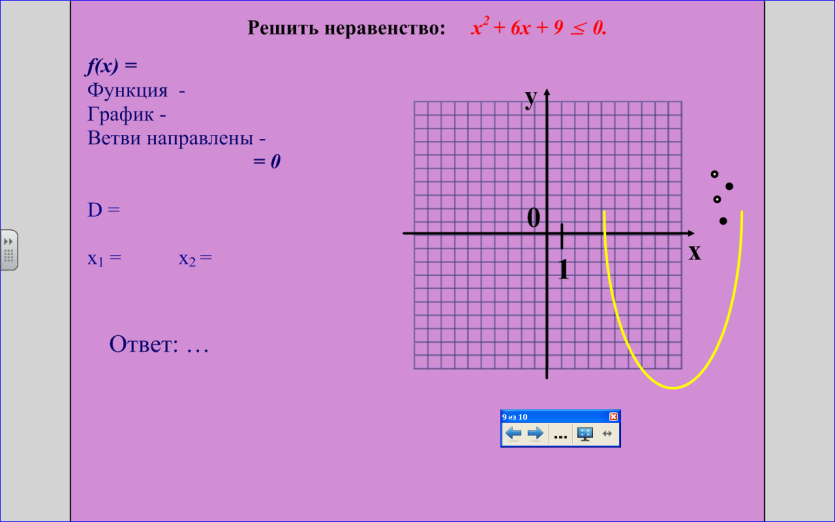
Решение задач на тренажёре, встроенном в презентацию. ( гиперссылки – треугольники ).
VI. Самостоятельная работа. ( задание на карточках) проверка ( рис. 12 )
VII. Домашнее задание. ( рис. 13 )
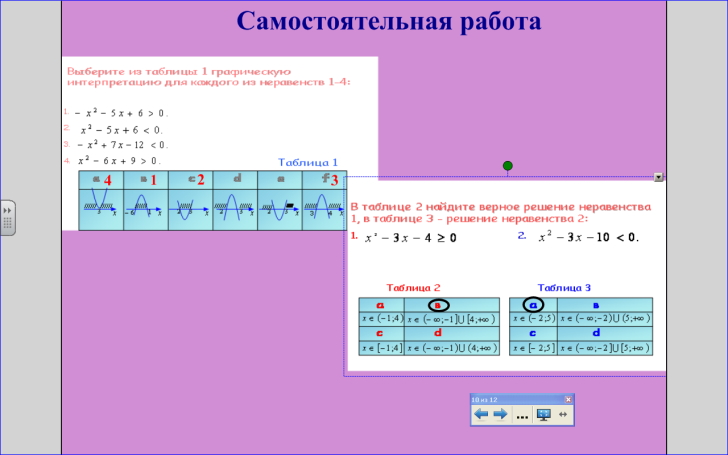

Рис.13
Рис.12
VIII. Итог урока. Оценки. ( рис. 14 )
Рис.14
Спасибо за урок!