Урок алгебры в 9 классе по теме «Свойства корней степени n»

Михайлова Галина Ивановна

Учитель математики

МОУ-СОШ с. Карпенка Краснокутского района Саратовской области

Урок алгебры в 9 классе по теме

«Свойства корней степени n»

Тип урока: совершенствование умений и навыков.

Характеристика темы: Преподавание ведётся по учебнику “Алгебра 9” Никольского С.М. для общеобразовательных учреждений. На данную тему отводится 3 часа. Это третий урок.

Дидактическая цель урока: Научить применять полученные знания при решении различных задач, в том числе повышенного уровня сложности, стимулировать учащихся к овладению рациональными приемами и методами решения.

Образовательная цель урока: Обеспечить в ходе урока закрепление материала о свойствах корней степени n и применение этих свойств при выполнении упражнений.

Развивающая цель урока: Развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи учащихся.

Воспитательная цель урока: Воспитывать интерес к математике как учебному предмету через современные технологии преподавания, приучать к умению выслушивать других, умению общаться, прививать аккуратность и трудолюбие.

Формы работы организации познавательной деятельности: фронтальная, индивидуальная.

Оборудование. Компьютеры. Программа компьютерного тестирования Knowing (представляет собой удобную программу для тестирования с возможностью составления тестов и автоматической оценки результатов тестирования).

Ход урока.

1. Организационный момент.

2. Актуализация прежних знаний.

1. Какие из следующих записей не имеют смысла?

; ; ;

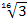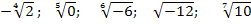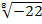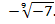
1. При каких значениях переменной а выражение имеет смысл?

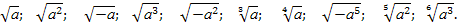
1. _{Вычислите:}

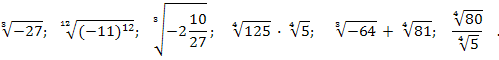
2. Проверка домашнего задания.

1. _{Формирование умений и навыков.}

1. _{Упростить выражение}

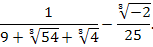
_{Решение.}

_{Преобразуем знаменатель дроби:}

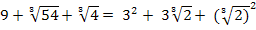– это неполный квадрат суммы чисел 3 и 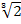. Чтобы избавиться от иррациональности в знаменателе дроби, умножим ее числитель и знаменатель на разность этих чисел: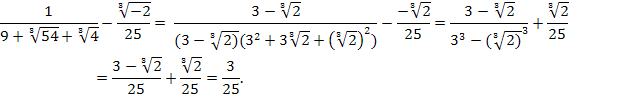

1. Упростить выражение 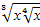и найти его значение при х= 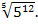_{Решение.}

_{Так как х≥0 ( в противном случае выражение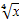} не имеет смысла), то .

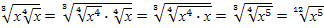Тогда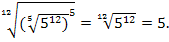

1. _{Найти значение выражения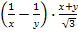} при х=.

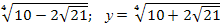Решение.

Преобразуем данное выражение при х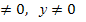( в противном случае данное выражение не имеет смысла):

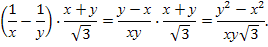
При заданных значениях х и у имеем

.

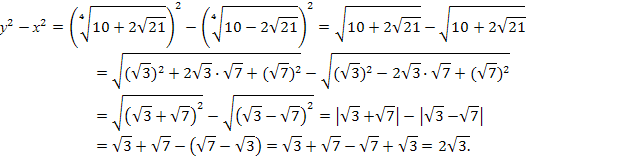
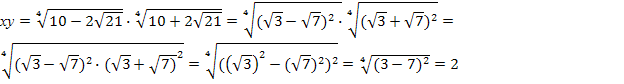Значит,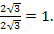

1. а) Вынести множитель из-под знака корня 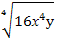при условии, что х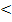0.

б) Внести множитель под знак корня 3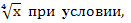учто у.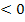

Решение.

а) Так как х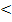0 по условию, а у 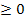(в противном случае выражение не имеет смысла), то =

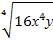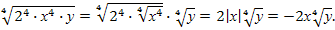
б) Так как у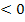 по условию, а х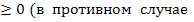не имеет смысла выражение 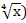, то

3у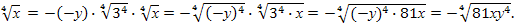

4.Самостоятельная работа (компьютерное тестирование).

Приложение 1.

Приложение 2.

5. Подведение итогов урока.

6.Домашее задание. П.4.6, №553, 555.

7. Использованная литература.

1. С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин .

Алгебра 9 класс – М.: Просвещение, 2009 г

1. М.К. Потапов, А.В. Шевкин. Дидактические материалы для 9 класса – М.: Просвещение, 2008 г

2. Воробьева Е.А. Алгебра. 9 класс. Проверочные работы с элементами тестирования. – Саратов: Лицей, 2008

3. Воробьева Е.А. Алгебра. 9 класс: В 2 ч. – Саратов: Лицей, 2008

4. Капитонова Т.А. Алгебра. 9 класс: Проверочные и контрольные работы. – Саратов: Лицей, 2006