Урок – обобщение по теме «Квадратные уравнения»
Конева Надежда Александровна, учитель математики ВКК
МБОУ Борисоглебского городского округа
средней общеобразовательной школы №4
Тип урока: урок закрепления знаний, презентация мини проектов.
Цель урока: повторить понятия, связанные с квадратным уравнением, способами решения различных квадратных уравнений и уравнений, сводящихся к квадратным.
Задачи урока:
Образовательные: повторить определения, связанные с понятием квадратного уравнения и способами решения; осуществить контроль знаний с помощью проверочных заданий.
Развивающие: способствовать развитию внимания, развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях.
Воспитательные: воспитывать информационную культуру, самостоятельность, умение слушать.
Методы обучения:
систематизирующий;
наглядно-иллюстративный;
проектный;
использование идеи самоанализа с систематическим применением самоконтроля учащихся.
Урок проводится в форме «живой газеты». Итогом урока является выпуск газеты по рубрикам урока.
Оборудование:
Компьютер и мультимедийный проектор
Авторская и ученическая презентации к уроку
Документ-камера
Ноутбуки для тестирования
Карта результативности.
Используемый УМК Макарычева Ю.Н. «Алгебра 8 класс»
Этап подготовки к уроку - домашнее творческое задание:
«Из истории квадратных уравнений» - сообщения, презентация. Выпуск листовок и
практических советов по решению задач. Составление теста по теме урока в программе – конструкторе тестов easyQuizzy.
Рубрики газеты:
1. Теория в кластерах
2. Первичное подтверждение теории в виде теста, составленного в программе – конструкторе тестов easyQuizzy
3. Практические советы (и не только советы) по решению задач и уравнений.
4. Исторические сюжеты о квадратных уравнениях
5. Следствие ведут знатоки
6. Сделай свой выбор
Каждая рубрика имеет свой эпиграф. По каждой рублике –листовка наклеивается на страницу «живой газеты»
Оценки выставляем в карту результативности за работу в каждой рубрике.
Карта результативности:
Ф.И.
Теория
в кластерах
Тест
Практика
Сам. работа
Зад.3
Исторические
сюжеты -проекты
Следствие ведут знатоки
ИТОГ
Зад.1
Зад.2
Найди ошибку
Устная работа
Оценка
Ход урока.
Начав изучать квадратные уравнения, вы уже успели заметить, что информация о корнях уравнения скрыта в коэффициентах. Сегодня мы продолжим разговор о «тайнах» квадратных уравнений, и сделаем это в форме «живой газеты». Живая газета – это газета, которую создадите вы. Однако, любая газета читаема тогда, когда в ней интересная и полезная информация, актуальные дискуссии, мнения и комментарии. И вы, ребята, будете корреспондентами сегодняшнего выпуска. В нашей газете будет несколько рубрик, каждая из которых имеет эпиграф. Открывает сегодняшнюю полосу газеты:
Рубрика I. Теория в кластере: «Виды квадратных уравнений».
Теория без практики мертва и бесплодна, практика без
теории невозможна и пагубна
А. Н. Крылов
Заполните кластер и сдайте на проверку.(слайды 1,2)
Ф.И.
коэффициенты
полное
неполное
приве-
денное
неприве-
денное
биквад-
ратное
а
в
с
1. х4 + 5х2 +3 = 0
2. 6х2 + 9 = 0
3. х2 – 3х = 0
4. –х2 + 2х +4 = 0
5. 3х + 6х2 + 7 =0
Квадратным уравнением называется …
Приведенное квадратное уравнение – это…
Неполное квадратное уравнение – это…
Запиши формулу дискриминанта. Запиши количество корней уравнения корней и формулу для их нахождения, если D>0.
Ответь на вопрос о количестве корней при D=0, запиши формулу для их нахождения.
Ответь на вопрос о количестве корней, если D<0
Самопроверка по ключу в презентации, самооценка и результат выставляется в карту результативности.
Рубрика II «Первичное подтверждение теории»: тестирование на компьютерах.
В тесте 5 заданий. Перемешивая задания и ответы программа предлагает задания к выполнению. Количество полученных баллов является оценкой за тест. Оценки выставляем в карту результативности.
«Залог успеха – огромное внимание»
Тест в программе easyQuizzy(требуется открыть программу, заранее установленную на компьютерах). Задания будут появляться в различной последовательности, но состоять из предлагаемых:
Назови коэффициенты квадратного уравнения : 4х2 -3х +1=0
a=4, b= - 3, c =1; 2) a=- 3, b=4, c =1; 3) a=1, b= - 3, c =4; 4) a=1, b= 4, c =-3.
Реши уравнение: х2 – 13 х + 36 = 0 удобным способом. Ответ запиши без пробелов через точку с запятой в порядке возрастания корней.
Установи соответствие между квадратным уравнением и его коэффициентами:
А) 3х2 -7х+ 4=0; Б) 4х2 +3х –7=0; В) -7х2 +3х +4=0
1)a=4, b= 3, c = - 7; 2) a=3, b=-7, c =4; 3) a=-7, b= 3, c =4;
Одно из двух натуральных чисел больше другого на 5. Найди эти числа, если их произведение равно 24.
1)2 и 12; 2) 4 и 6; 3) 3и 8; 4) 1 и 24.
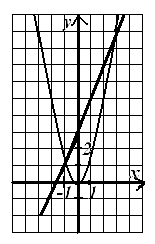
5. Уравнение х2-2х-3=0 решили графически. Определи по рисунку корни уравнения, записав ответ без пробелов через точку с запятой в порядке возрастания.
Рубрика III. «Практика – источник знаний и критерий истины»
Данную рубрику открывают практические советы
по решению задач с помощью квадратных уравнений, с которыми нас знакомят ребята, готовившие данные советы (слайд №4):
Переведи условие задачи с русского языка на математический язык
Построй математическую модель задачи (составь уравнение )
Реши уравнение
Исследуй корни уравнения (удовлетворяют ли они условию задачи)
Проанализируй решение задачи (рассмотри другие варианты решения, выбери наиболее рациональное решение )
Запиши ответ
Задачи рубрики:
1.Составьте условие задачи и математическую модель по чертежу на спортивную тематику и решите её (работа фронтальная) (слайд №5)
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.» ( У. У. Сойер) (слайд №6) 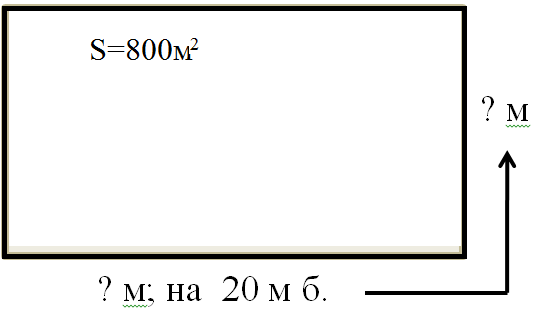
2. Решите уравнение х2 - 4х + 3 = 0 различными методами. (слайд №6) (Ответ: -1; -3) У доски 5 обучающихся. Метод, которым придется решать, написан в произвольно выбираемой карточке: 1) по общей формуле; 2) по формуле с четным вторым коэффициентом; 3) по теореме Виета; 4) по сумме коэффициентов; 5) выделением квадрата двучлена; 6) графический метод (через документ – камеру решает 6-ой обучающийся). У каждого обучающегося, решающего у доски, есть группа поддержки в виде ряда учеников, которые решают на местах уравнение тем же способом. Т.о. получается группа из 4-5 обучающихся, занятых решением одинаковым способом.
После решения анализируем и делаем вывод, каким из способов проще и быстрее решить данное уравнение.
Выполняем самооценку и результат выставляем в карту результативности.
3. Решите биквадратное уравнение: х4 -10х2 + 9 = 0 (слайд №7) (самостоятельная работа)
Решение: Замена: х2=t, то решением уравнения t2 -10t + 9 = 0 являются числа t1= 9, t2=1. Выполнив обратную замену, имеем два неполных квадратных уравнения: х2 =9 и х2=1. Решением первого неполного квадратного уравнения служат числа -3 и 3, решением второго – числа -1 и 1.
Ответ: -3; -1; 1; 3
Выполняем проверку работы соседа, оцениваем его работу и заносим результат в карту результативности.
Рубрика IV. Исторические сюжеты о квадратных уравнения
(открыть презентацию, которая вложена в архив её изображение на слайде №8)
В истории черпаем мы мудрость, в поэзии – остроумие, в математике – проницательность
Роджер Бэкон
Оценки за рубрику в карту результативности выставляют те учащиеся, которые были заняты проектной работой и результат мини исследования представили в виде презентации, встроенной в основную.
Рубрика V. Следствие ведут знатоки(слайд №9)
В математике нет символов для неясных мыслей
Анри Пуанкаре
Найди ошибку в решении квадратного уравнения
2х2+36х+130=0 | : 2
х2+18х+65=0
a=1, k=9, c=65
D1= k2 – ac
D1= 92 - 1·65 = 81 – 65 = 16
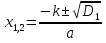
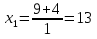
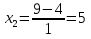
Ответ: 5; 13
Реши уравнения устно(используя свойства коэффициентов квадратного уравнения)
383х2 – 385х + 2 = 0;
5х2 + 9х –14 = 0;
х2 + 29х – 30 = 0;
х2 - 2000х – 2001 = 0;
72х2 + 69х – 3 = 0;
83х2 – 97х + 14 = 0.
341х2+290х-51=0
67х2-75х+8=0
19х2+15х-34=0
Рубрика VI. Сделай свой выбор(слайд №10)
Итог: - Какова особенность сегодняшнего урока?
- Не работали по учебнику и повторили методы решения квадратных уравнений и рассмотрели особенности их решения. Перечислим эти методы: 1) по общей формуле; 2) выделением квадрата двучлена; 3) по формуле с четным вторым коэффициентом; 4) по теореме Виета; 5) по сумме коэффициентов; 6) графический метод.
Домашнее задание вы узнаете, найдя дискриминант уравнения: 3/4х2 +21х – 71=0. В данном номере 8 квадратных уравнений, при решении которых должны присутствовать все способы, о которых шла речь. Выбор остаётся за вами.