ЗАДАЧИ С ПАРАМЕТРОМ для 11 класса.
(из сборника «ТЕСТОВЫЕ ЗАДАНИЯ ДЛЯ ПОДГОТОВКИ К ЕГЭ-2008» под редакцией Е.А.СЕМЕНКО)
Все рассматриваемые задания в сборнике являются заданиями С3 части 3.
Вариант 1
Найти все значения параметра а, при которых в области определения функции
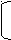
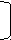 у =
у =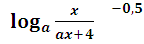
есть натуральные числа, но ни одно из них не делится на 7.
Решение.
у= 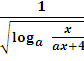
D(у): 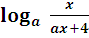 >0.
>0.
Рассмотрим 2 случая:
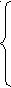 a >1,
a >1,
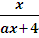 > 0,
> 0,
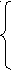
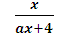 >1;
>1;
a >1,
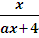 - 1> 0;
- 1> 0;
 a >1,
a >1,
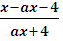 > 0;
> 0;
 a >1,
a >1,
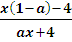 > 0;
> 0;
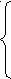 a >1,
a >1,
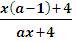 < 0;
< 0;
Решим 2-ое неравенство методом интервалов:
а) х(а-1) + 4=0, б) ах + 4=0,
х =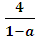 . х =
. х = 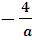 .
.
Сравним числа 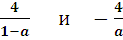 при а>1:
при а>1:
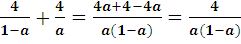 < 0, т.к.1- а < 0
< 0, т.к.1- а < 0
Значит, 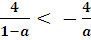
в





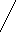

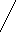




 )
) 





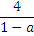
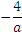
x
х є (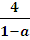 ;
; 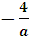 ) при а >1.
) при а >1.
Очевидно, что на этом промежутке расположены только отрицательные числа, а значит, среди них нет натуральных чисел, и условие задачи не выполняется.
 0
0
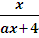 >0,
>0,
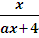 <1;
<1;
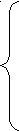 0
0
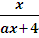 >0,
>0,
 <0;
<0;
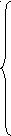 0< a<1,
0< a<1,
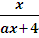 >0,
>0,
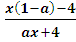 < 0.
< 0.
При 0< а <1 1- а>0, и значит 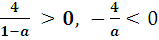 .
.
Решим 2-ое неравенство системы методом интервалов:














0
x


Решим 3-е неравенство системы методом интервалов:




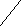










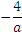
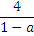
x
Итак, х є (0; 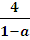 ), при а є (0;1)
), при а є (0;1)
Ясно, что этот промежуток содержит натуральные числа.
Чтобы эти числа не делились на 7, необходимо выполнение следующих условий :

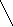




0 1
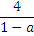
7 х


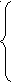
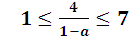 ,
,
0< a <1;
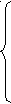
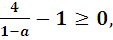
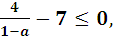
0< a < 1;
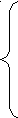
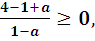
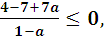
0< a < 1; т.к. а < 1, то 1- а > 0
 а + 3≥ 0,
а + 3≥ 0,
7а - 3≤ 0,
0 < а < 1;
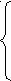 -3≤ а ≤
-3≤ а ≤ ,
,
0 < а < 1; т.е. а є (0;  ).
).
Ответ: а є (0; 3/7)
Вариант 2.
Найдите все значения параметра а, при которых уравнение
4х+2( а-3)2х+5-а=0 не имеет корней.
Решение:
Пусть 2х = t, t>0, тогда уравнение примет вид:
t2 +2(a-3)t+5-a=0.
Решим это уравнение при t>0, и определим, при каких значениях а, оно не имеет корней.
Возможны 2 случая:
Квадратное уравнение не имеет корней, если D<0
D=(a-3)2-(5-a)=a2-6a+9-5+a=a2-5a+4=(a-1)(a-4),
(a-1)(a-4)<0, a є (1; 4)
2)Данное в условии уравнение не будет иметь корней, если квадратное уравнение относительно t имеет корни, но они не удовлетворяют условию t > 0, т.е. t ≤ 0.
 Итак, D ≥ 0,
Итак, D ≥ 0,
t1 +t2 ≤ 0,
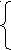 t1 • t2 ≥ 0.
t1 • t2 ≥ 0.
По теореме Виета t1+ t2= -2(a-3),
t1 • t2= 5-a.
З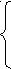 начит, (a-1)(a-4) ≥ 0,
начит, (a-1)(a-4) ≥ 0,
-2(a-3) ≤ 0,
5-a ≥ 0;
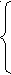 (a-1)(a-4) ≥ 0,
(a-1)(a-4) ≥ 0,
a-3 ≥ 0,
a ≤ 5;
 (a-1)(a-4) ≥ 0,
(a-1)(a-4) ≥ 0,
3≤ a ≤ 5;





+
+
--



1 3 4 5 a

а є [4;5].
Итак, условие задачи выполняется, если
а є (1; 4) [4; 5] = (1; 5].
[4; 5] = (1; 5].
Ответ: а є (1; 5]
Вариант 3
Найдите все значения параметра а, при которых множество решений неравенства
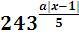 • 32x-a >
• 32x-a > 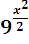
содержит ровно 6 целых чисел.
Решение:
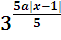 •
• 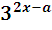 >
> 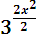 ,
,
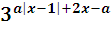 >
> 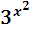
Т.к. функция у=3t монотонно возрастает на (-∞; +∞), то большему значению аргумента соответствует большее значение функции, поэтому:
a|x-1|+ 2x-a > x2,
x2 -2x- a|x-1|+a< 0.
Е
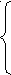 сли х ≥ 1, то |x-1|= x-1;
сли х ≥ 1, то |x-1|= x-1;
х2-2x- a(x-1)+a<0,
x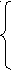 ≥ 1;
≥ 1;
x2- (2+a)x+2a<0,
x ≥ 1;
( x-2)(x-a)<0,
x-2)(x-a)<0,
x



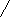
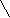
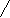

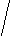 ≥1.
≥1.
Е









а 1 2 х
 сли а<1, то:
сли а<1, то:
х є [1; 2)
Е







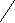

1 2 х





 сли а=1, то:
сли а=1, то:
х є (1; 2)
Е






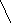
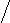







 сли а є (1; 2), то:
сли а є (1; 2), то:
1 а 2 х
х є (а; 2)Если а = 2, то неравенство (х-2)2<0 не имеет решений
Е

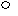




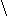
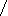




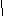 сли а > 2, то:
сли а > 2, то:
х
1 2 а х
 є (2; а).
є (2; а). 2)Если х<1, то |x-1|=1-x
x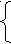 2-2x- a(1-x)+a<0,
2-2x- a(1-x)+a<0,
x <1;
x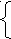 2-(2-a)x <0,
2-(2-a)x <0,
x <1;
x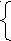 (x-(2-а))<0,
(x-(2-а))<0,
x < 1.
Решим 1-ое неравенство системы методом интервалов, рассмотрев различные случаи взаимного расположения точек х=0 и х = 2-а
Е

 сли 2-а<0, т.е. а>2, то:
сли 2-а<0, т.е. а>2, то:












2-а 0 1 х

х є (2-а; 0)
Если 2-а=0, т.е. а=2, то1-ое неравенство системы примет вид х2<0, которое не имеет решений.
Если 0< 2-а <1, т.е. а є (1; 2), то:















0 2-а 1 х

х є (0; 2-а)
Если 2-а=1, т.е. а=1, то














0 2-а=1 х
х є (0; 1)
е
 ) Если 2-а>1,т.е. а<1, то
) Если 2-а>1,т.е. а<1, то







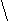
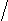




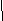
0 1 2-а х

х є (0;1)
Итак,
При а<1, х є (0;1)
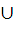 [1;2)=(0; 2). Это множество решений не содержит 6 целых чисел, значит, условие задачи не выполняется.
[1;2)=(0; 2). Это множество решений не содержит 6 целых чисел, значит, условие задачи не выполняется.При а =1, х є (0; 1)
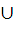 (1; 2). В этом множестве нет целых чисел вообще.
(1; 2). В этом множестве нет целых чисел вообще.При а є (1;2), х є (0; 2-а)
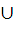 (а; 2), где так же нет целых чисел
(а; 2), где так же нет целых чиселПри а =2, неравенство не имеет решений.
При а >2, х є (2-а; 0)
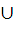 (2; а).
(2; а).
Это множество представляет собой объединение двух промежутков одинаковой длины |a-2|, каждый из которых должен по условию задачи содержать ровно 3 целых числа. На промежутке (2;а)- это числа: 3; 4; 5. Значит, а ≤ 6.
На промежутке (2-а; 0)-это числа:-1; -2; -3. Значит, 2-а < -3,
т.е. а > 5.
Итак, а є (5; 6]
Ответ : а є (5; 6]
Вариант 4
Найдите все значения параметра а, при которых в области определения функции y= 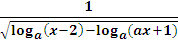
нет ни одного натурального числа, квадрат которого больше либо равен 144.
Решение:
D(y): loga(x-2) - loga(ax+1)>0,
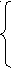 loga(x-2) > loga(ax+1)
loga(x-2) > loga(ax+1)
x-2>0,
ax+1>0;
Рассмотрим 2 случая:
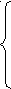 a>1,
a>1,
x-2> ax+1,
x-2 > 0,
ax+1 > 0;
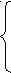 a>1,
a>1,
x(1-a) > 3,
ax > -1; т.к. а>1, то 1-а<0, тогда:
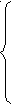 a > 1,
a > 1,
х < 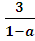 ,
,
x > 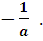
Оба числа  и
и 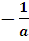 являются отрицательными, сравним их при а >1:
являются отрицательными, сравним их при а >1:
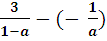 =
= 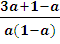 =
= 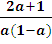 < 0, т.к. а > 1
< 0, т.к. а > 1
Значит,  <
< 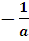





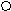
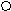

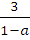 -
-  x
x
Решений нет; т.е. область определения функции - пустое множество; в таких случаях говорят, что функция не определена, а значит, условие задачи не выполняется.
 0< a <1,
0< a <1,
x-2 < ax+1,
x-2 >0;
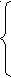 0< a< 1,
0< a< 1,
x(1-a)< 3,
x >2;
т.к. а є (0; 1), то 1-а>0,
 0
0
х <  ,
,
x > 2.
При всех а є (0; 1) числа  >3
>3









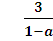
2
x
Итак, х є (2;  ) при а є (0; 1).
) при а є (0; 1).
По условию задачи в D(у) не должно быть ни одного натурального числа, квадрат которого был бы больше либо равен 144. Значит, число 12 не должно находиться внутри этого промежутка, т.е.
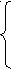
 ≤ 12,
≤ 12,
0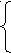 < a< 1;
< a< 1;
3 ≤ 12(1-a),
0< a <1;
1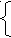 2a ≤ 9,
2a ≤ 9,
a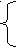 ≤ 3/4,
≤ 3/4,
0< a< 1.
Итак, a є ( 0; 3/4]
Ответ: а є (0; 0,75]
Вариант 5
Найдите все значения параметра а, при которых уравнение
3|8-x| =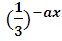 имеет ровно один корень, принадлежащий отрезку [3; 9].
имеет ровно один корень, принадлежащий отрезку [3; 9].
Решение:
3|8-x| = 3ax
Т.к. функция у=3t монотонно возрастает на (-∞; +∞), тогда
|8-x|=ax, или |x-8|=ax.
Решим уравнение графически.

у




У=|x-8|
y=ax, a=a2


х
5
y=ax, a=a1


0

8 9
1 3

у = ах - множество прямых, проходящих через начало координат и имеющих различные угловые коэффициенты.
Если а=0, то графики функций у=0 и у=|х-8| пересекаются при х= 8, 8 є [3; 9]
Из рисунка видно, что имеются два предельных положения прямой у = ах, таких, чтобы она пересекала график функции у=|х-8| в одной точке с абсциссой, принадлежащей отрезку[3; 9].
Итак, а1 < а ≤ а2,
где а1 = tg α1 = 1/9,
a2 = tg α2 =5/3.
Значит, данное уравнение имеет один корень из промежутка [3; 9], если
а є 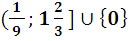
Ответ : а є (1/9; 5/3] 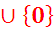
Вариант 6
Найдите все значения параметра а, при которых в области определения функции
у =
есть натуральные числа, кратные 5, но ни одно из кратных 5 не делится на 9.
Решение:
logax - loga(ax+1) ≥0,
logax ≥ loga(ax+1).
1)если а >1, то функция у=loga t возрастает на (0;+∞),поэтому:
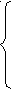 a >1,
a >1,
x >0,
ax+1>0,
x ≥ ax+1;
a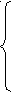 >1,
>1,
x >0,
x >-1/a,
(1-a) x ≥1;т.к. при а >1, (1-а)<0, то:
a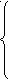 >1,
>1,
x >0,
x ≤ 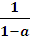 .
.
Очевидно, что система не имеет решений, т.к. 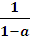 <0 при а>1. Значит, при а>1функция не определена, и условие задачи не выполняется.
<0 при а>1. Значит, при а>1функция не определена, и условие задачи не выполняется.
2)при а є (0;1) функция у=loga t убывает на (0;+∞), значит
 0 < a <1,
0 < a <1,
х >0,
ax > -1,
x ≤ ax+1;
 0< a <1,
0< a <1,
X >0,
(1-a) x ≤ 1;
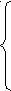 0< a <1,
0< a <1,
х > 0,
х ≤ 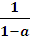 .
.
Т.к. 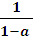 >0 при а є (0; 1), то х є (0;
>0 при а є (0; 1), то х є (0; 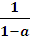 ] при а є (0; 1).
] при а є (0; 1).
Итак, D(f) = (0; 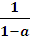 ], a є (0; 1)
], a є (0; 1)
Чтобы в области определения функции содержались числа, кратные 5, необходимо выполнение неравенства:
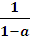 ≥ 5.
≥ 5.
Но, чтобы эти числа не были кратны 9, необходимо выполнение неравенства: 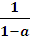 < 45.
< 45.
И так, 0< a<1,
так, 0< a<1,
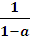 ≥5,
≥5,
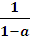 <45;
<45;
Т.к. 0
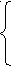 0
0
1 ≥ 5(1-a),
1 <45(1-a);
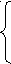 0< a <1,
0< a <1,
5a ≥ 4,
45a < 44;
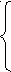 0
0
а ≥ 4/5,
a< 44/45, т.е. а є [4/5; 44/45)
Ответ: а є [4/5; 44/45)
Вариант 7
Найдите все значения параметра а, при которых в области определения функции
y=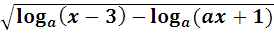
есть натуральные числа, кратные 3, но ни одно из кратных 3 не делится на 7.
Ответ: а є [1/3; 17/21)
Указания:
При а >1 D(f) - пустое множество, значит функция неопределенна.
П


 ри а є (0; 1) D(y) = (3;
ри а є (0; 1) D(y) = (3;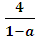 ]. Чтобы в D(y) содержались числа, кратные 3, но не кратные 7, необходимо, чтобы
]. Чтобы в D(y) содержались числа, кратные 3, но не кратные 7, необходимо, чтобы
6 ≤ 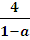 < 21.
< 21.
3 6 7 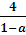 21 x
21 x
Решив неравенство 6 ≤ 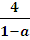 < 21 при а є (0;1), получим ответ.
< 21 при а є (0;1), получим ответ.
Вариант 8
Найдите все значения параметра а, при которых уравнение
25х+2(а+1)5х+1-5а=0 не имеет корней.
Ответ: а є (-7; 0,2).
Указания:
Условие задачи выполняется, если 1) D<0; или 2) D ≥0, но корни соответствующего квадратного уравнения неположительны, тогда по т. Виета 2(а+1) ≥ 0 и 1-5а ≥ 0.
Вариант 9
При каких значениях параметра а уравнение
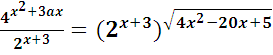
имеет ровно три различных корня?
Решение
Т.к. 4х2 - 20х + 25=(2х-5)2, то уравнение примет вид: 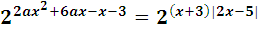
Т.к. функция у=2t монотонно возрастает на (-∞; +∞), то:
2ах2+6ах-(х+3)=(х+3)| 2х-5 |,
2ах(х+3)-(х+3)=(х+3)| 2х-5 |,
(2ах-1)(х+3)=(х+3)|2x-5|,

 х+3=0,
х+3=0,
 2ах-1=| 2х-5|.
2ах-1=| 2х-5|.
Значит, х = -3 – один из корней данного уравнения.
Решим уравнение 2ах-1=|2x-5 | графически, и найдем значения параметра а, при которых это уравнение имеет только 2 корня.
Р
азделим на 2 обе части этого уравнения, и построим графики функций у= ах и у =|x-2,5| +0,5

y
Y=ax, a=1

Y=|x-2,5|




1
Y=ax, a=a1



1 2,5 x
x
Очевидно, что графики функций будут пересекаться в двух точках, если
а є (а1; 1)
Причем, абсциссы точек пересечения будут больше 1,5, а, значит, никогда не примут значение х = -3; поэтому все корни уравнения будут различны.
Найдем а1: а1=tg α=0,5:2,5=0,2
Итак, уравнение имеет 3 различных корня, если а є (0,2; 1)
Ответ: а є (0,2; 1).
Вариант 10
Найдите все значения параметра а, при которых в области определения функции
y =
есть натуральные числа, кратные трем, но ни одно из кратных трем не делится на 5.
Ответ: а є (0; 0,8]
Указания:
D(у): loga(x-1)-loga(ax+1)>0
1)Функция неопределенна при а>1
2)D(у)= (1;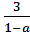 ) при ає(0;1)
) при ає(0;1)
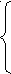 3<
3<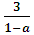 ≤15,
≤15,
0<а<1.
Вариант 11
Найдите все значения параметра а, при которых уравнение
lg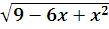 +lg(x+1)=lg(ax2+(2+a)x+2) имеет два различных корня.
+lg(x+1)=lg(ax2+(2+a)x+2) имеет два различных корня.
Решение:
lg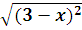 +lg(x+1)=lg(ax2+(2+a)x+2),
+lg(x+1)=lg(ax2+(2+a)x+2),
l g(|3-x|•(x+1))=lg(ax2+(2+a)x+2)
g(|3-x|•(x+1))=lg(ax2+(2+a)x+2)
|3-x|>0,
x+1>0,
ax2+(2+a)x+2>0;
x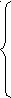 >-1,
>-1,
x ≠3,
ax2+(2+a)x+2>0,
| x-3|(x+1)=ax2+(2+a)x+2;
Т.к. х > -1, то |x-3|(x+1)>0
x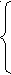 >-1,
>-1,
x ≠ 3,
|x-3|(x+1)= ax2+(2+a)x+2.
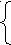 -1< x<3,
-1< x<3,
(3-x)(x+1)= ax2+(2+a)x+2;
 -1< x<3,
-1< x<3,
-x2+2x+3= ax2=2x+ax+2;
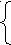 -1< x<3,
-1< x<3,
(a+1)x2+ax-1=0;
 -1< x <3,
-1< x <3,

 x = -1,
x = -1,
 x =
x = 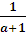 ;
;
-1< 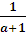 <3,
<3,
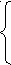
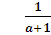 > - 1,
> - 1,
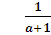 <3;
<3;
-2 -1 a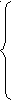

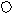
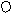


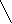
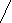


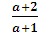 > 0,
> 0,
-1 -2/3 -2 a

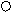


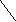
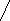


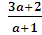 > 0.
> 0.
а є (-∞;-2)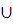 (-2/3;+∞)
(-2/3;+∞)
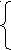
x>3,
(x-3)(x+1)=ax2+(2+a)x+2;
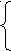 x>3,
x>3,
x2-2x-3-ax2-2x-ax-2=0;
 x >3,
x >3,
(1-a)x2-(a+4)x-5=0;
Т.к. 1- а-5= - (а+4), то х1= -1, что не удовлетворяет условию х >3;
х2 = 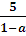 ,
, значит:
значит:



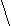
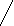
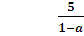 > 3,
> 3,






-  1 a
1 a


 > 0 .
> 0 .  а є(-2/3;1)
а є(-2/3;1)
И

так,
х

-2 -  a
a
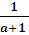

x

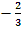 1 a
1 a
2 =
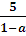
Уравнение имеет 2 различных корня, если а є (-2/3; 1)
Ответ: а є (-2/3; 1)
Вариант 12
При каких значениях параметра а уравнение
 имеет три различных корня?
имеет три различных корня?
Решение:
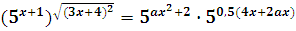 ,
,
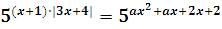 ,
,
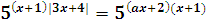 .
.
Т.к. показательная функция у=5t монотонно возрастает на (-∞; +∞), то:
(х+1)|3x+4|=(ax+2)(x+1),
x
 =-1,
=-1,
| 3x+4|=ax+2;
3x+4|=ax+2;
значит, х = -1 – один из корней уравнения.
Решим уравнение |3x+4|=ax+2 графически, и определим значения параметра а, при которых графики функций у=|3х+4| и у=ах+2 пересекаются в двух точках.
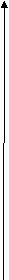
у

У=|3x+4|
Y=ax+2, a=a2



2







х
Y=ax+2, a=a1
-1
Очевидно, что графики функций будут пересекаться в двух точках, если ає (а1; а2),
а1=tgα1=-3:1= -3,
a2=tgα2=2: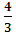 =
=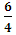 =1,5
=1,5
Итак, ає (-3;1,5); но следует исключить те значения а, при которых абсцисса точки пересечения графиков равна -1
Если х= -1, то: |3(-1)+4|=a(-1)+2,
|-3+4|=-a+2,
a=1.
Значит, а є (-3;1)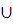 (1;1,5)
(1;1,5)
Ответ: а є (-3;1)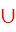 (1;1,5)
(1;1,5)
Вариант 13
Найдите все значения параметра а, при которых в области определения функции
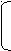
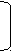 y=
y= 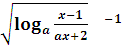
нет ни одного натурального числа, квадрат которого больше либо равен 121.
Решение:
у = 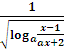
D(y): 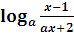 >0,
>0,
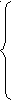 a>1,
a>1,
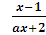 >0,
>0,
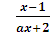 >1;
>1;
a >1,
>1,
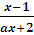 >1;
>1;
a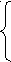 >1,
>1,
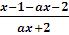 >0;
>0;
a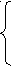 >1,
>1,
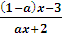 >0.
>0.
Решим 2-ое неравенство системы методом интервалов. Сравним числа  и
и 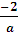 при а>1:
при а>1:
 +
+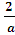 =
= 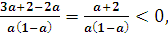
Значит, 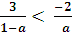 при а>1
при а>1



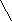
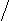
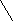









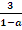
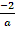
x
х є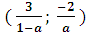 при а>1.
при а>1.
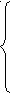 0
0
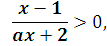
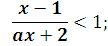
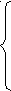
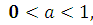
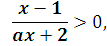
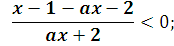
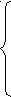
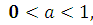
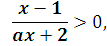
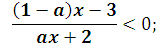
Решим неравенства системы методом интервалов.
При а є (0;1) число 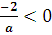 , число
, число 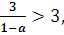 а, значит и больше 1.
а, значит и больше 1.



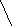
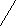
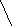
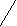













x



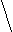









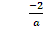 1
1 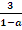 x
x

х є (1;  ) при а є (0;1)
) при а є (0;1)
Итак, при а > 1 D(у)=
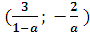 ;
;
при а є (0; 1) D(у)=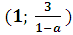
По условию задачи, в области определения функции не должно находиться ни одно натуральное число, квадрат которого больше либо равен 121.
При а >1 в D(у) нет положительных чисел, а, значит, нет и натуральных чисел; поэтому при а > 1 условие задачи выполняется.
При а є (0; 1) в D(у) могут содержаться натуральные числа. Первое число, квадрат которого равен 121, это 11. Значит, необходимо выполнение условий:
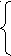





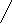
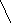
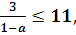
0
1 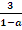 11 x
11 x
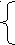 3≤ 11-11a,
3≤ 11-11a,
0< a<1;
1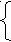 1a ≤ 8,
1a ≤ 8,
0< a<1;
a ≤
≤ 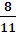 ,
,
0< a <1.
а є (0; 8/11].
Ответ: а є (0; 8/11]
Вариант 14
Найдите все значения параметра а, при которых уравнение
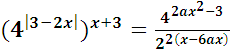
имеет единственный корень.
Решение:
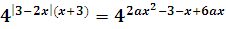 ,
,
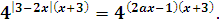
Т.к. функция у=4t монотонно возрастает на(-∞; +∞), то:
|
 3-2x|(x+3)=(2ax-1)(x+3),
3-2x|(x+3)=(2ax-1)(x+3),
x=-3,
|2x-3|=2аx-1.
О чевидно, что х = -3 - один из корней уравнения, и, чтобы он был единственный, необходимо, чтобы 2-ое уравнение системы не имело корней.
чевидно, что х = -3 - один из корней уравнения, и, чтобы он был единственный, необходимо, чтобы 2-ое уравнение системы не имело корней.
Разделим 2-ое уравнение совокупности на 2 и преобразуем его к виду: |x-1,5|+0,5=ax .
Решим его графически, и определим значения параметра а, при которых графики функций у = |x-1,5|+0,5 и у = ах не пересекаются.


у

Y=|x-1,5|+0,5




у=ах, а=а2
5




у=ах, а=а1
х
-3
Очевидно, что графики не пересекаются, если ає[а1; а2), где а1=tg α1 = -1,
a2=tg α2=0,5: 1,5=5: 15=1/3
Значит, а є [-1; 1/3)
Кроме того, следует добавить такие значения а, при которых графики пересекаются, но абсцисса точки пересечения равна -3.
х = -3:
|-3-1,5|+0,5=-3a,
|-4,5|+0,5=-3a,
-3a=5,
a=-5/3.
Итак, а є [-1; 1/3)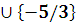
II способ (аналитический)
|2x-3|(x+3)=(2ax-1)(x+3),
x
 = -3,
= -3,
| 2x-3|=2ax-1.
2x-3|=2ax-1.
Решим 2-ое уравнение совокупности:
Если х ≥ 1,5, то |2x-3|=2x-3,
2x-3 = 2ax-1,
2x-2ax = 2,
(1-a)x = 1.
а) при а=1 уравнение не имеет корней;
б) при а≠1 уравнение имеет один корень х = 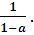
Необходимо выполнение условия: х ≥ 1,5, т.е.
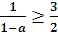 ,
,
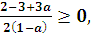
 .
.



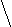







1/3 1
a



а є [1/3;1).
Если х < 1,5, то |2x-3|=3-2x,
3-2x = 2ax-1,
2ax+2x = 4,
(a+1)x = 2.
а) приа = -1 уравнение не имеет корней;
б) при а ≠ -1 уравнение имеет один корень х = 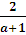 .
.
Необходимо выполнение условия: х <1,5, т.е. 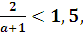
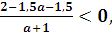
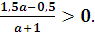














-1 1/3 a
а є (-∞; -1)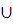 (1/3; +∞).
(1/3; +∞).
Итак, х = 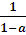 при a є [1/3; 1);
при a є [1/3; 1);
х = 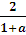 при a є (-∞ ; -1)
при a є (-∞ ; -1)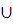 (1/3; +∞);
(1/3; +∞);
x = -3 при а є R.
Выясним, при каких значениях параметра а корни совпадают.
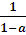 = -3,
= -3,
1 = -3(1-a),
3a =4,
a=4/3 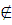 [1/3; 1),
[1/3; 1),
значит корень 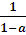 ни при каких значениях а не равен -3.
ни при каких значениях а не равен -3.
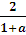 = -3,
= -3,
2= -3(1+а),
3а=-5,
а= -5/3, значит, при а= -5/3 корни совпадают.





 х =
х =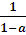
1/3 1 a


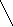
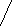
х

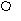

-5/3 -1 1/3 a
=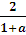
х
a
=-3
Очевидно, что исходное уравнение имеет один корень
х= - 3 при а є [-1; 1/3) 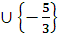
Ответ: а є [-1; 1/3) 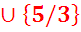
Вариант 15
Найдите все значения параметра а, при которых уравнение
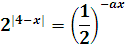
имеет ровно два корня, принадлежащих отрезку [2; 6].
Решение.
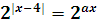 ,
,
|x-4|=ax.
Решим уравнение графически, построив графики функций
y=|x- 4| и y=ax


у
у =ах, а=1
у=|x-4|
у=ах, а є (а1;1)

у=ах, а=а1
4
2





х
1 2 4 6
х0
Очевидно, что при а=1 графики пересекаются в одной точке с абсциссой
х = 2, значит, условие задачи не выполняется.
При а = 0 у = ах совпадает с Ох и графики функций также пересекаются в одной точке с абсциссой х = 4, и условие задачи не выполняется.
При а є (0; 1) графики пересекаются в двух точках, но, если а є (а1;1), то одна из абсцисс точек пересечения не принадлежит отрезку[2; 6]
Значит, условие задачи выполняется, и графики пересекаются в двух точках с абсциссами, принадлежащими [2;6], если а є (0; а1],
где а1=tgα = 2/6=1/3
Ответ: а є(0; 1/3]
Стр.