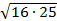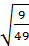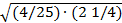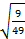Урок по алгебре в 8 классе.
Учитель: Патрина Татьяна Николаевна, МОУ СОШ №120 с углубленным изучением отдельных предметов Московского района города Казани
Тема: «Применение свойств квадратных корней».
Вид урока: закрепление материала по теме «Свойства квадратного корня».
Цель урока: Уметь применять свойства квадратных корней к преобразованию выражений и решению уравнений.
Тип урока: комбинированный.
Формы и методы работы:
индивидуальная работа по карточкам,
фронтальная (решение тестов),
эвристический.
Оборудование урока:
карточки (4 варианта), тесты (2 варианта),
учебник (справочный материал на форзаце учебника).
экран, проектор.
Ход урока:
Актуализация знаний учащихся.
Показ отрывка презентации ученицы 10 класса Ахметзяновой Виктории «Как извлечь корень?», исторические данные.
Повторение свойств.
Ученик записывает свойства на доске и проговаривает их:
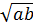 =
= 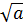 ∙
∙ 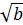 , a≥0,b≥0;
, a≥0,b≥0; 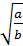 =
= 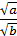 , a≥0, b>0;
, a≥0, b>0; 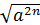 =│ап│, пN.
=│ап│, пN.
Индивидуальная работа у доски (4 человека), остальной класс работает с тестами (4 задания, 2 варианта).
Карточки, для работы у доски:
Карточка 1
Карточка 2
Карточка 3
Карточка 4
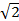 ∙
∙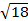
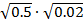
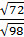
1. (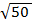 +
+ 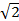 )2
)2
2. (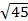 -
-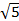 )2
)2
ответы
1. 20; 2. 3/7; 3. 3/5.
1. 3; 2. 0,1; 3. 6/7.
1. 11; 2. 61.
1. 72; 2. 20.
Тест для работы на местах:
Вариант 1
Вычислить.
1.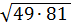
а)63; б)48; в)42; г)21.
2. 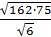
а)42; б)45; в)1/42; г)15.
3. 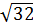 ∙
∙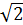
а)32; б)15; в)8; г)16.
4. 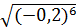 .
.
а)0,8; б)-0,008; в)0,008; г)0,016.
Вариант 2
Вычислить.
1.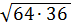
а)63; б)48; в)42; г)94.
2. 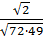
а)42; б)45; в)1/42; г)1/36.
3. 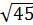 ∙
∙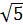
а)8; б)15; в)25; г) 16.
4. –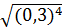 .
.
а)-0,9; б)0,09; в)-0,09;г) 0,06.
Проверка работы у доски и на местах. Оценивание работ.
Закрепление материала. Решение заданий.
Задание на доске (дети пытаются решить самостоятельно):
Упростите выражение
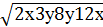 , х≥0, у≥0.
, х≥0, у≥0.Докажите, что
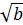 =13
=13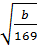 (мой вопрос в конце решения: какое условие должно быть для
(мой вопрос в конце решения: какое условие должно быть для 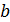 ?)
?)
Решение заданий из учебника:
(Доп. главы) стр.118, №402 (в,г), 403 (в,г). Учащиеся решают в тетрадях 2 чел. с № 402 у доски, № 403 за доской 2 чел.
Вычислить:
Задания на экране. Учащиеся решают самостоятельно, 2 человека у доски с заданиями №2 и №3.
(
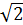 – 1)(
– 1)(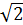 + 1)(
+ 1)(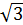 -
- 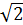 )(
)(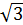 +
+ 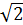 )…(
)…(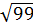 +
+ 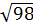 ). (отв.1)
). (отв.1)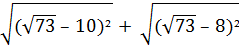 . (отв.2)
. (отв.2)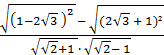 . (отв.-2)
. (отв.-2)
Упростить:
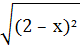 +
+ 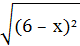 , если 3 ≤ х ≤ 5. (отв.4)
, если 3 ≤ х ≤ 5. (отв.4)
А теперь давайте поиграем
Тест «Пасьянс»
Решить задания (строчки 1 и 2) и найти ответы в остальных строчках
(задания на экране, проверка там же)
задания
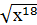 , х < 0
, х < 0
(-2∙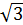 )2
)2
5∙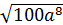
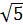 ∙
∙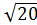
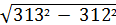
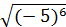
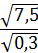
(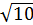 -
-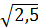 )²
)²
ответы
-125
3,5
50
х9
5
2
6
125
50а6
12
- х16
5
-х9
50а4
10
-2,5
25
(мои слова: Решим несколько заданий на определение квадратного корня, повторение.)
Сколько корней имеют данные уравнения (устно, задание на экране):
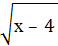 +
+ 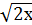 = 0; ответ: 0;
= 0; ответ: 0;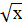 = х; ответ: 2 корня (х=0 и х=1)
= х; ответ: 2 корня (х=0 и х=1)(х - 1)² +
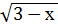 + 1 = 0? ответ: 0.
+ 1 = 0? ответ: 0.
Решите уравнения: (письменно в тетрадях, задание на экране):
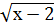 = 1, ответ: х=3;
= 1, ответ: х=3;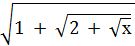 = 2, ответ: х=49.
= 2, ответ: х=49.х² - а = 0 (Решение этого уравнения разбирается на доске).
х² - а = 0
х² = а
х = 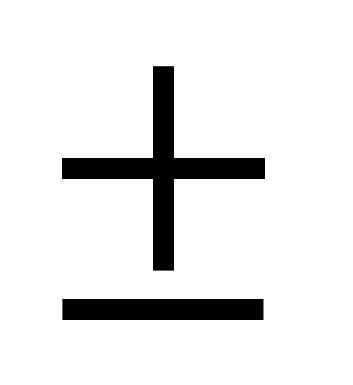
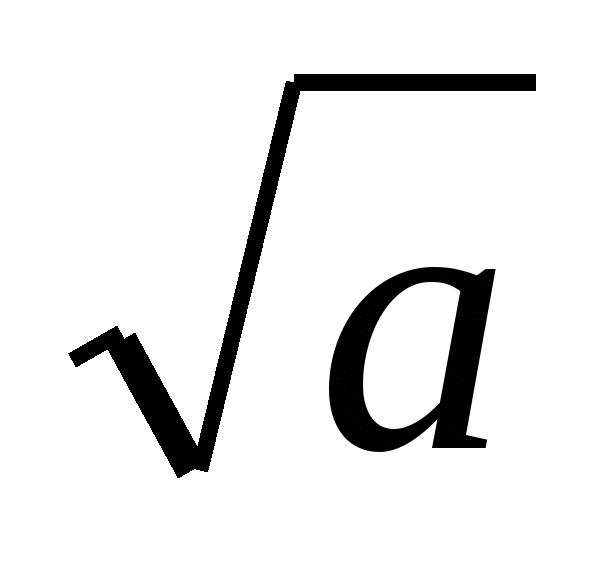 сколько корней уравнения?
сколько корней уравнения?
Два, если а>0; один, если а=0; нет корней, если а<0
Уравнения, в которых некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами называются уравнениями с параметрами. В дальнейшем мы с вами научимся решать уравнения такого вида.
Заключение:
Выставление оценок.
Домашнее задание:
доп. главы №407 и №623 (задачник)
Учебная литература:
1. А.Г.Мордкович, «Алгебра 8» ч.1,2, М., «Мнемозина», 2008 г.,
2. Ю.Н.Макарычев, Н.Г.Миндюк, «Дополнительные главы к учебнику Алгебра 8», М., «Просвещение», 2008 г.
Раздаточный материал:
Тест по теме «Свойства квадратных корней»
Вариант 1
Вычислить.
1.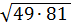
а)63; б)48; в)42; г)21.
2. 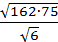
а)42; б)45; в)1/42; г)15.
3. 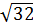 ∙
∙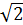
а)32; б)15; в)8; г)16.
4. 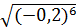 .
.
а)0,8; б)-0,008; в)0,008; г)0,016.
Вариант 2
Вычислить.
1.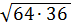
а)63; б)48; в)42; г)94.
2. 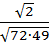
а)42; б)45; в)1/42; г)1/36.
3. 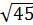 ∙
∙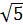
а)8; б)15; в)25; г) 16.
4. –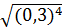 .
.
а)-0,9; б)0,09; в)-0,09;г) 0,06.
Карточки для работы у доски:
Карточка 1
Карточка 2
Карточка 3
Карточка 4
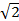 ∙
∙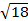
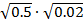
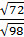
1.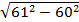
2.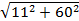
1.(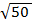 +
+ 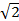 )2
)2
2. (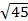 -
-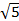 )2
)2