Урок по теме
« Логарифмическая функция. График и свойства»
Цели урока
Образовательные:
Ввести понятие логарифмической функции.
Дать определение.
Начать формировать умения построения графика логарифмической функции.
Применять приемы преобразования графика.
Формировать умение работать с тестом.
Развивающие:
Развивать творческую и мыслительную деятельность учащихся.
Развивать способность к видению проблемы.
Формировать умения четко и ясно излагать свои мысли.
Воспитательная:
Воспитывать умение работать с имеющейся информацией
Воспитывать культуру общения, навыки самоконтроля
Умение работать в коллективе.
Основная педагогическая технология: технология развивающего и проблемного обучения.
Тип урока: открытие нового знания.
Оборудование: доска, мультимедийная установка, раздаточный материал.
Этапы урока:
1 Организационный момент
2 Проверка домашнего задания.
3 Актуализация опорных знаний.
4 Формирование новых знаний – постановка проблемы.
5 Формирование умений применение знаний для открытия новых свойств.
6 Первичное закрепление - работа с графиком.
7 Формирование новых знаний с опорой на известные преобразования.
8 итог урока. Рефлексия.
Ход урока.
1 этап: Организационный момент. Сообщение темы урока.( слайд1)
2 этап
Двое учащихся приглашаются к доске : задание вычислить значение :
1. Log 31 log 33 log 39 log 31/3 log 31/9
2. log1/3 1 log 1/33 log 1/39 log 1/31/3 log 1/31/9
Опрос домашнего задания:
-одному учащемуся предлагается построить график показательной функции с основанием 3 и записать все свойства: У=3Х
- второму - построить график функции у=(х-1)2 и построить график обратной функции, задать ее формулой.(Проверка домашнего задания)
3 этап
Пока трое учащихся готовятся , остальным учащимся предлагается выполнить тест с помощью слайдов.
Графики, каких функций изображены на слайде?
Решить уравнение3х =6
По графику функции определить промежутки возрастания
На каком рисунке изображен график у=(0,5)х-1
Какое из указанных чисел не принадлежит области определения выражения
log5 ( 0,36-х2)
Проверка осуществляется с помощью презентации. Если верно выполнен тест ,то получается Джон Непер- известный шотландский математик ,чье имя связано с открытием понятия логарифма числа.
Проверка домашнего задания на доске. Повторение определения обратной функции, ее свойств. Как выглядят графики обратных функций.
4 этап.
Обладает ли показательная функция свойствами, необходимыми чтобы иметь обратную? Обсуждение в группе.
у=ах и у=logах- как связаны эти функции между собой. Попробуйте придумать определение новой функции.
В тетрадь записывается определение логарифмической функции.
Логарифмическую функцию можно изучать как обратную к показательной функции. Рассмотрим другой подход к изучению свойств функции. Раньше мы по точкам строили график и по графику определяли свойства функции. А теперь рассмотрим другой подход : Зная свойства обратной функции ,построим ее график, используя свойства симметрии относительно прямой у=х.
5 этап .
Работа в группах. Учащиеся должны , используя график показательной функции, и свойства симметрии обратных функции относительно прямой у=х., построить логарифмическую функцию и по плану , предложенному учителем записать свойства



Область определения функции
Множество значения функции
Характеристическая точка
Промежутки возрастания , убывания, в зависимости от основания.
Вся проверка проходит с помощью презентации.
6 этап.
Учащиеся выполняют задание :
Построить графики двух функции у=log 3X и у=log 1/3X , используя табличку на доске, где учащиеся в начале урока вычисляли значения логарифмов. Записать основные свойства.
- Используя графики Выполнит ь задания : Сравнить
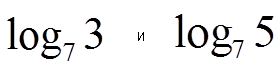
- Выяснить положительное или отрицательное число? log 3 4,5 log3 0,45,log1/32 Проверка с помощью слайдов.
7 этап
На основе имеющихся знаний о преобразовании графиков функции, построить следующие функции. Записать их свойства .Работа в парах. Можно пользоваться таблицей преобразования графиков.
У=log3(x-2) y= log 1/3 x-2 y= log3 (x+2)-3
Учащиеся выполняют задания , проверка проводится с помощью слайдов презентации.
8 этап Рефлексия: Фронтально учитель задает провокационные вопросы , в ходе ответов выясняется , что усвоено в процессе урока и на что нужно обратить внимание при выполнении домашнего задания.
Логарифмическая функция определена при любом х?
Областью значения логарифмической функцией является любое действительное число ?
Существует ли логарифм отрицательного числа?
Пересекает ли график логарифмической функции ось абсцисс?
Y=log3x -является убывающей.
Укажите картинку ,на которой изображен график логарифмической функции.
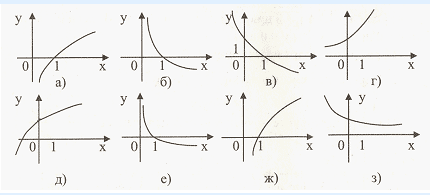
Постановка домашнего задания.