Автор: Морина Светлана Алексеевна.
Учитель математики МБОУ СОШ №5 города-курорта Железноводска
Урок по теме «Показательная функция»
Тип урока: урок изучения нового материала.
Цель урока: обеспечение условий для усвоения каждым учащимся знаний о показательной функции, её свойствах.
Задачи урока:
Образовательные задачи: ввести понятие показательной функции, рассмотреть ее свойства; научиться применять изученные свойства показательной функции в решении конкретных заданий и упражнений.
Развивающие задачи:
развивать умения сравнивать, обобщать, правильно формулировать задачи и излагать мысли;
развивать логическое мышления, внимание и умение работать в проблемной ситуации;
Воспитательные задачи:
Воспитывать интерес и любовь к предмету через содержание учебного материала, применение ЭОР, умение работать в коллективе, паре, взаимопомощи, культуры общения;
формировать у учащихся познавательный интерес;
воспитывать настойчивость в достижении цели.
Ход урока.
1. Орг. момент.
2. Изучение новой темы. 20 минут.
Фронтальная работа.(слайд 2)
- Эпиграфом нашего урока я хочу предложить слова Г. Лессинга «Спорьте, заблуждайтесь, ошибайтесь, но, ради Бога, размышляйте, и, хотя криво – да сами». Вам предстоит сегодня много рассуждать, делать выводы.
- В жизни мы часто сталкиваемся с зависимостями между величинами. Оценка по контрольной работе зависит от количества и правильности выполненных заданий, стоимость покупки от количества купленного товара и цен. Одни зависимости носят случайный характер, другие постоянны.
Д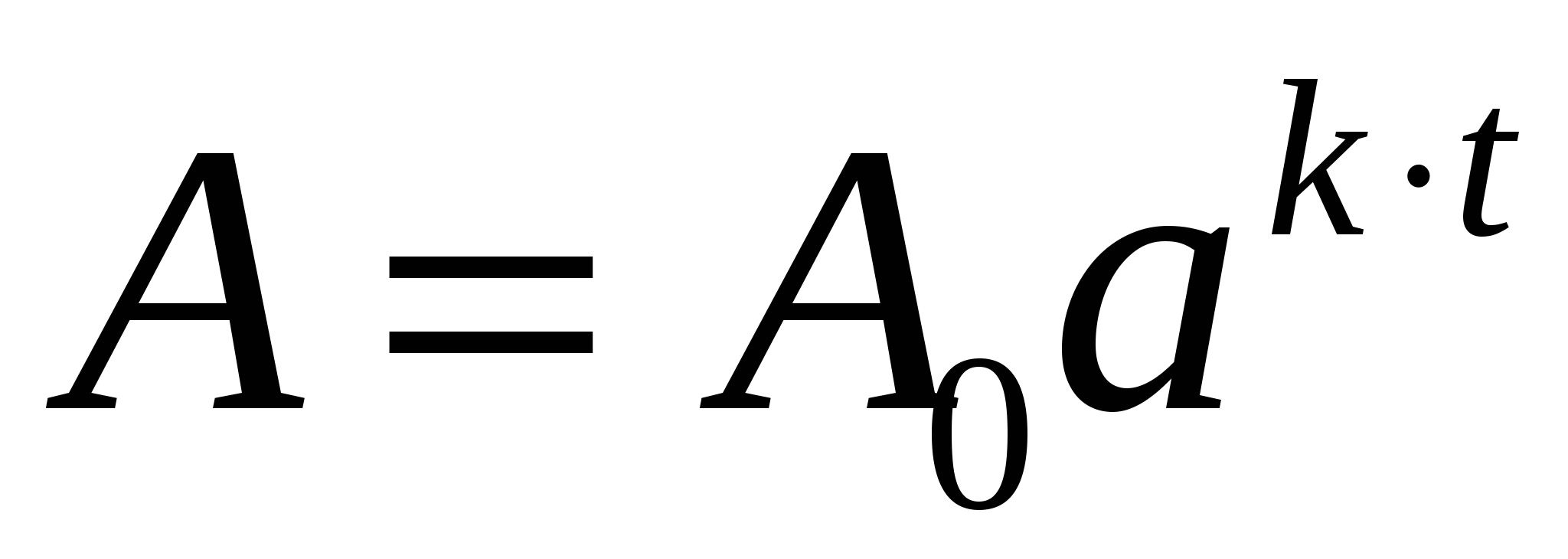
авайте рассмотрим следующие законы. (слайды 3)
Р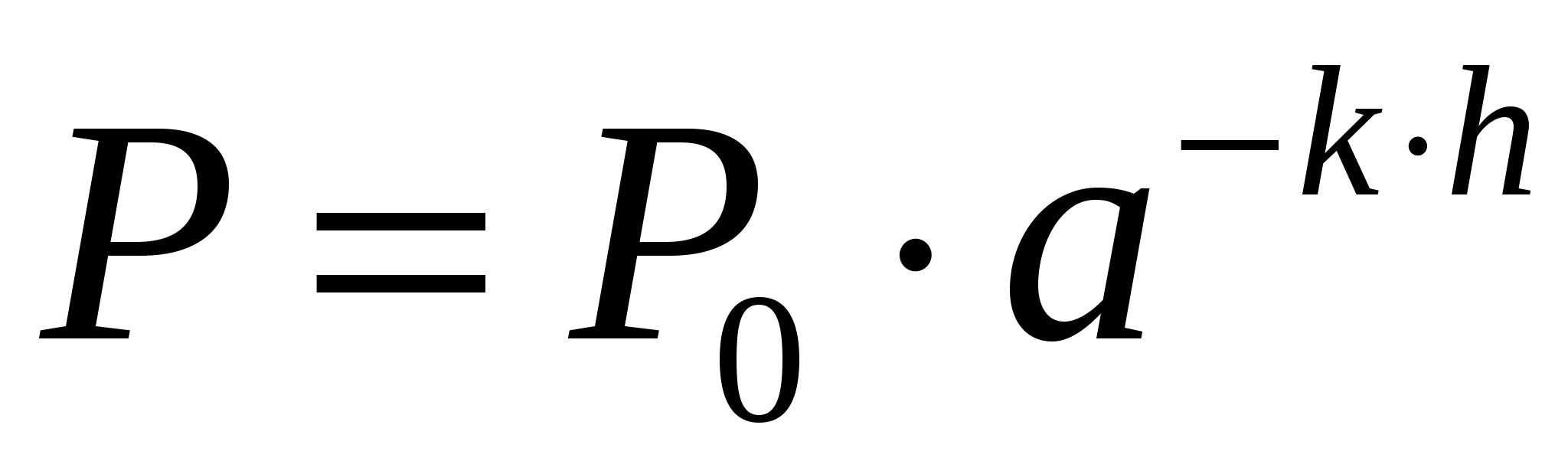
ост древесины происходит по закону:A- изменение количества древесины во времени;A0- начальное количество древесины; t-время, к, а- некоторые постоянные.
Давление воздуха убывает с высотой по закону: P- давление на высоте h,P0 - давление на уровне моря,а- некоторая постоянная.
-Что общее объединяет эти процессы? (дети отвечают, отмечая схожесть вида формулы, задающей закон)
-Положим в этих формулах с=1,к=1, какую функцию получим? (у=ах) (слайд 4)
- Такая функция называется показательной.(слайд 5)
- Сегодня на уроке, мы должны дать определение показательной функции, рассмотреть некоторые свойства и научится применять эти свойства при выполнении заданий, определенного вида.(слайд 6)
- Итак, попробуйте сформулировать определение показательной функции.
(учащиеся отвечают, учитель, если нужно корректирует определение).
(На слайде 7 появляется определение, учащиеся записывают его в тетрадь)
Практическая работа.(слайд8)
-В программе Excel построить графики функций у=2х (1 вариант), у=(1/2)х на отрезке[-2;3] с шагом 0,5. По предложенной схеме (слайд 9) исследовать функцию. (используются таблицы: график 1 вариант и график 2 вариант)
1. Область определения функции.
2. Область значений функции.
3. Точки пересечения с осями координат.
4.Промежутки возрастания и убывания.
(Учитель кратко проводит беседу по Технике безопасности при работе за компьютером. Учащиеся, работая в парах на компьютерах: составляют таблицу, вводят значения х, строят график функции и исследуют функцию по плану. Таблица «График 1 вариант» представлена так, как она выглядит в начале практической работы, а «График 2 вариант» - как в конце. Свойства функции записывают на листах.)
Проверка результатов практической работы.(слайды 10-11)
На экране появляются графики функций, учащиеся называют свойства, которые демонстрируются. Ученики делают записи в тетрадях.
4. Динамическая пауза. 1 минута
(гимнастика для глаз)
5. Закрепление изученного. 13 минут.
Устно.(учащиеся выбирают верный ответ, обосновывая выбор )(слайды 12-16)
1. Какая из предложенных формул задает показательную функцию?
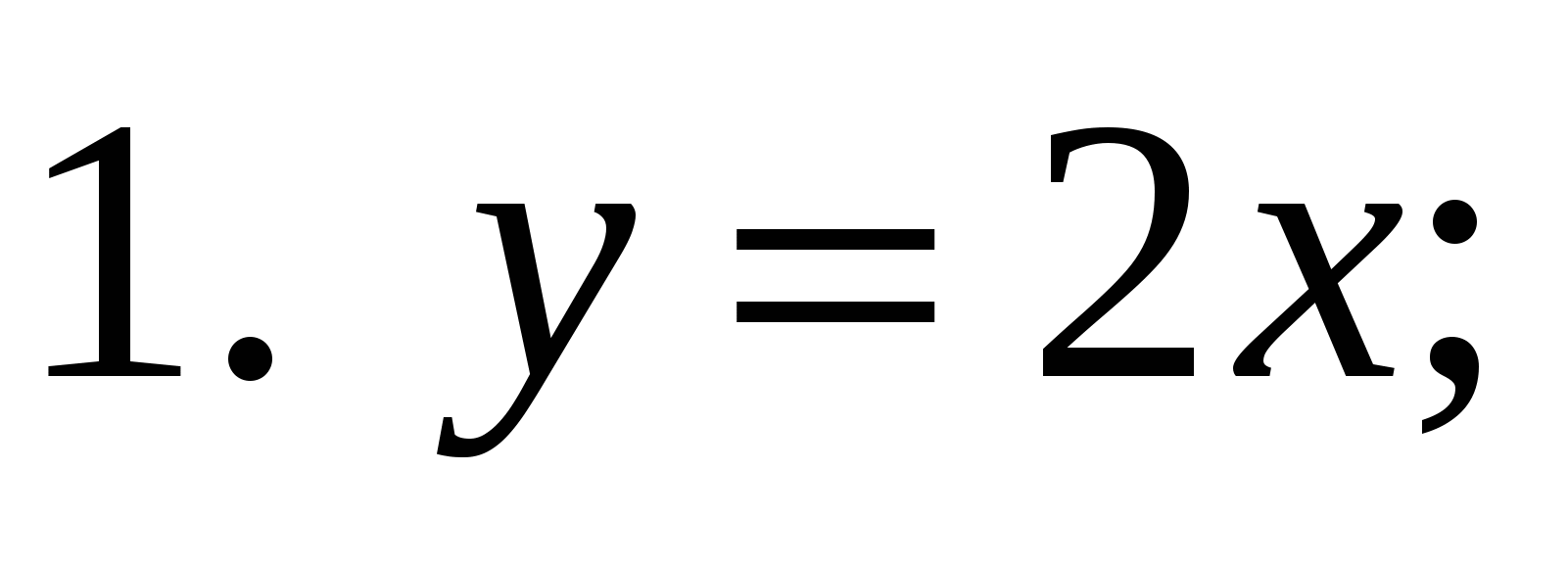
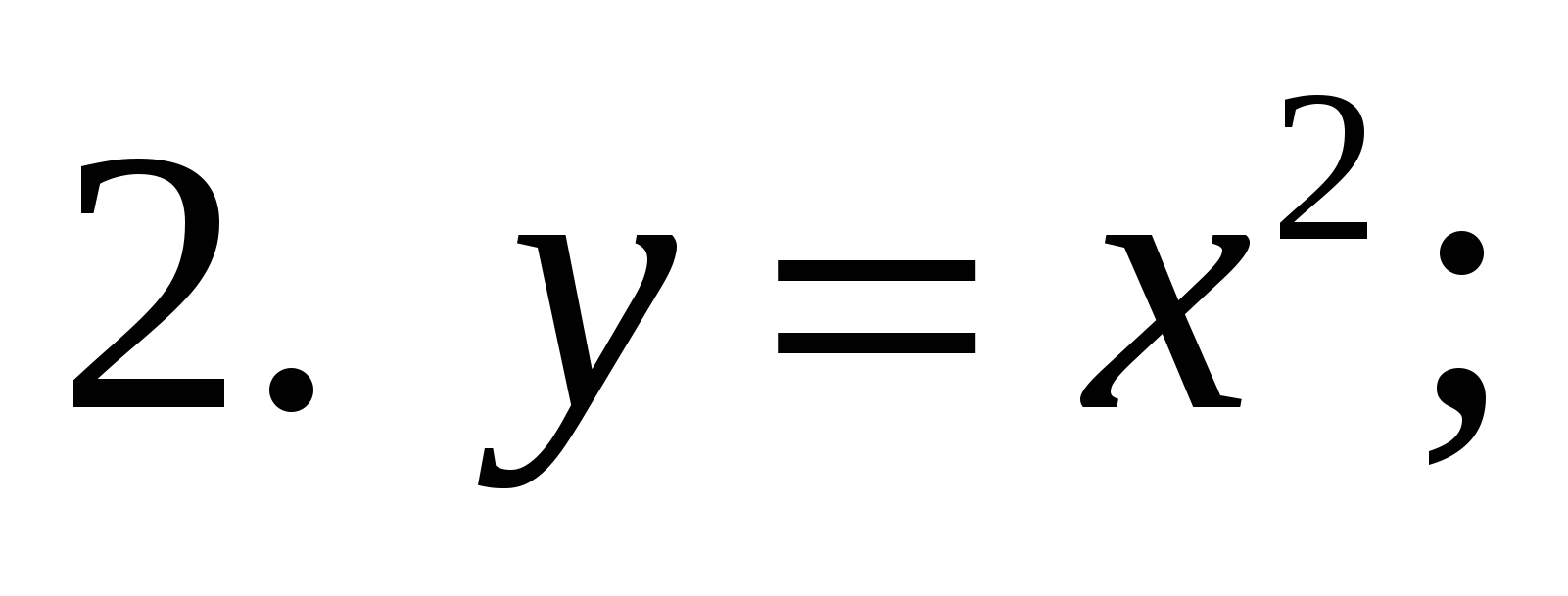
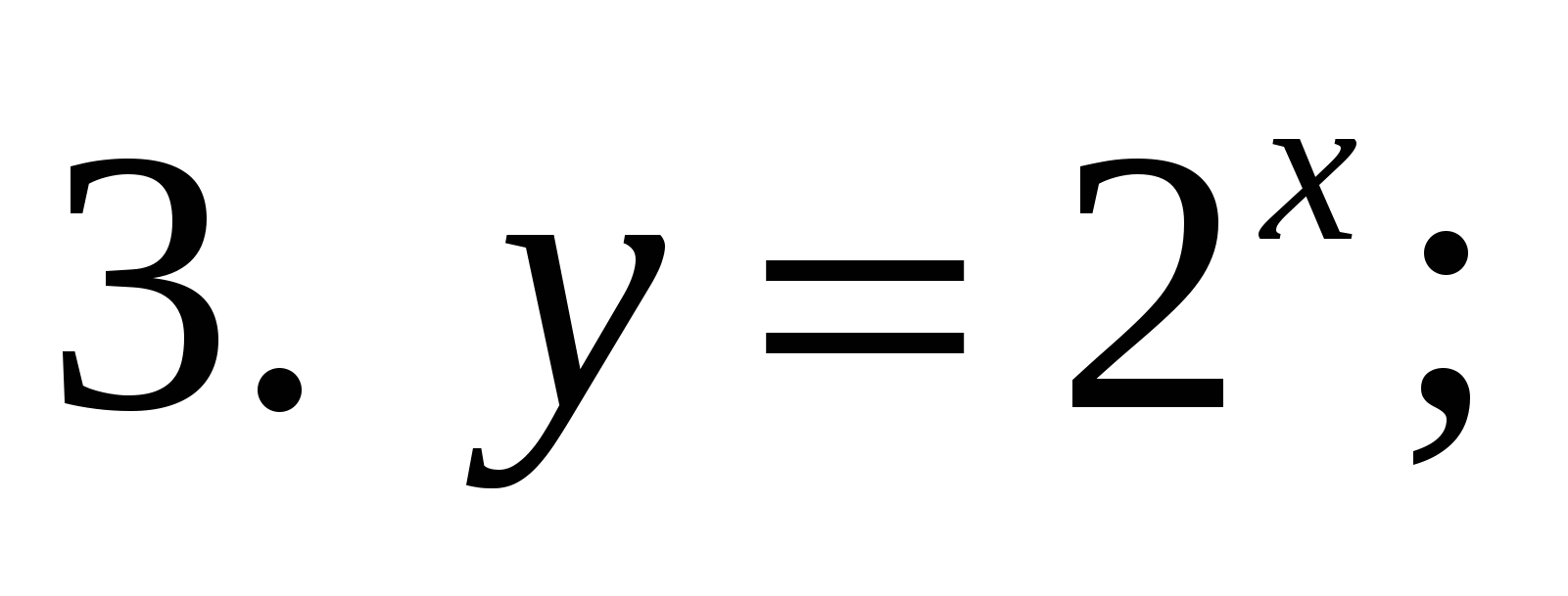
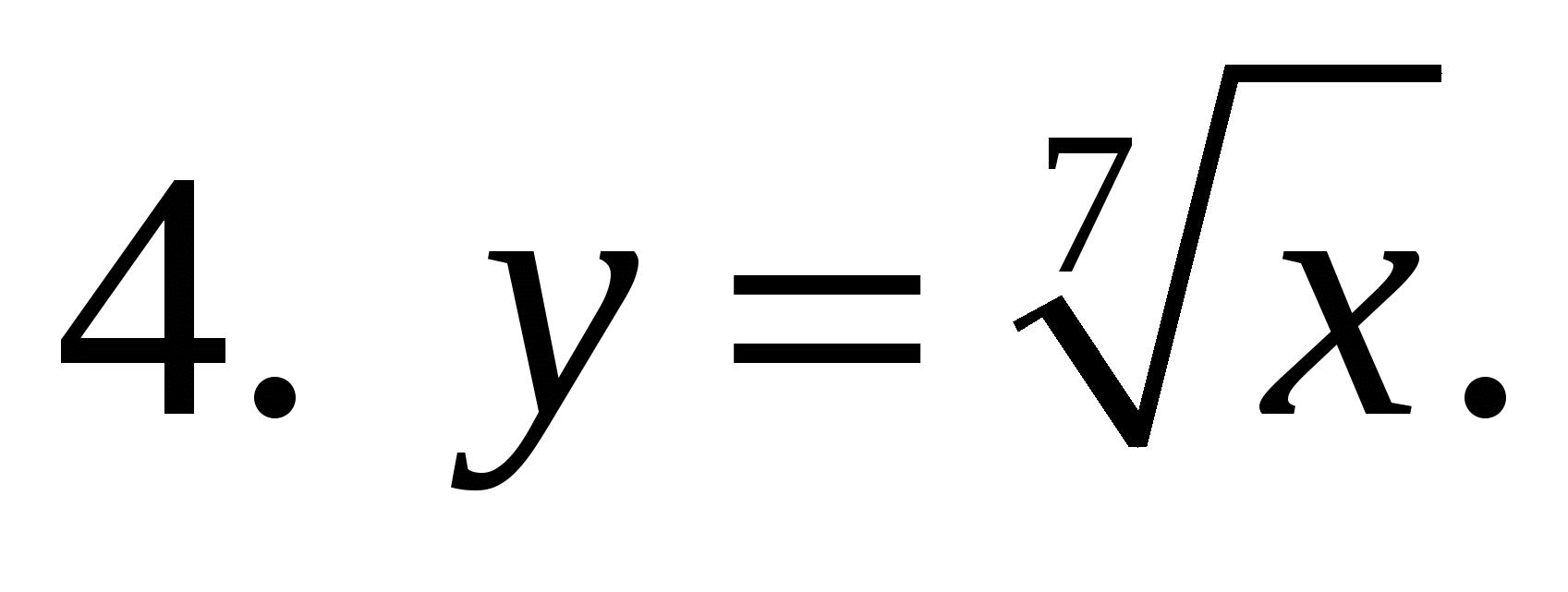
2. Дан график функции. Укажите эту функцию
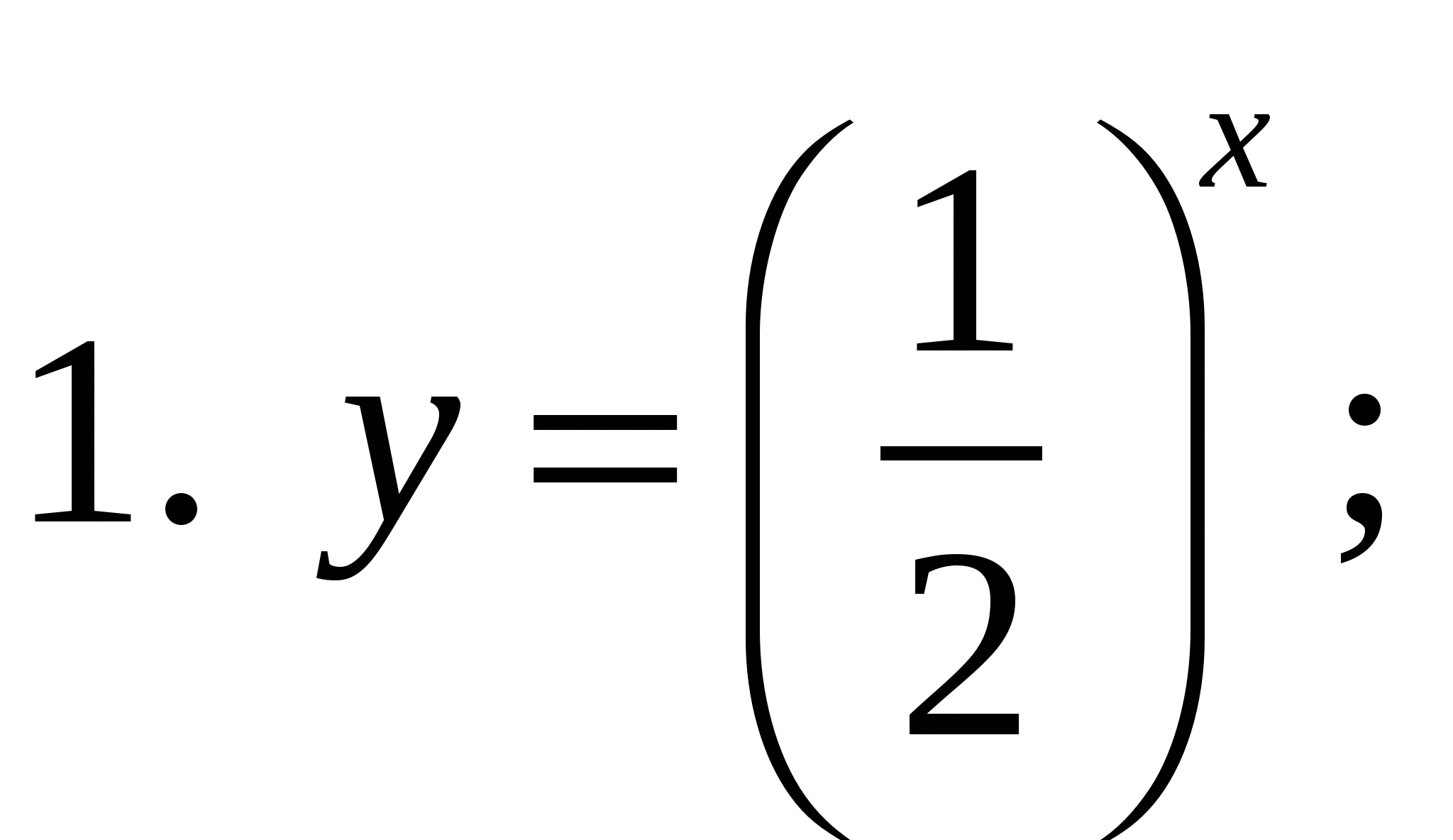
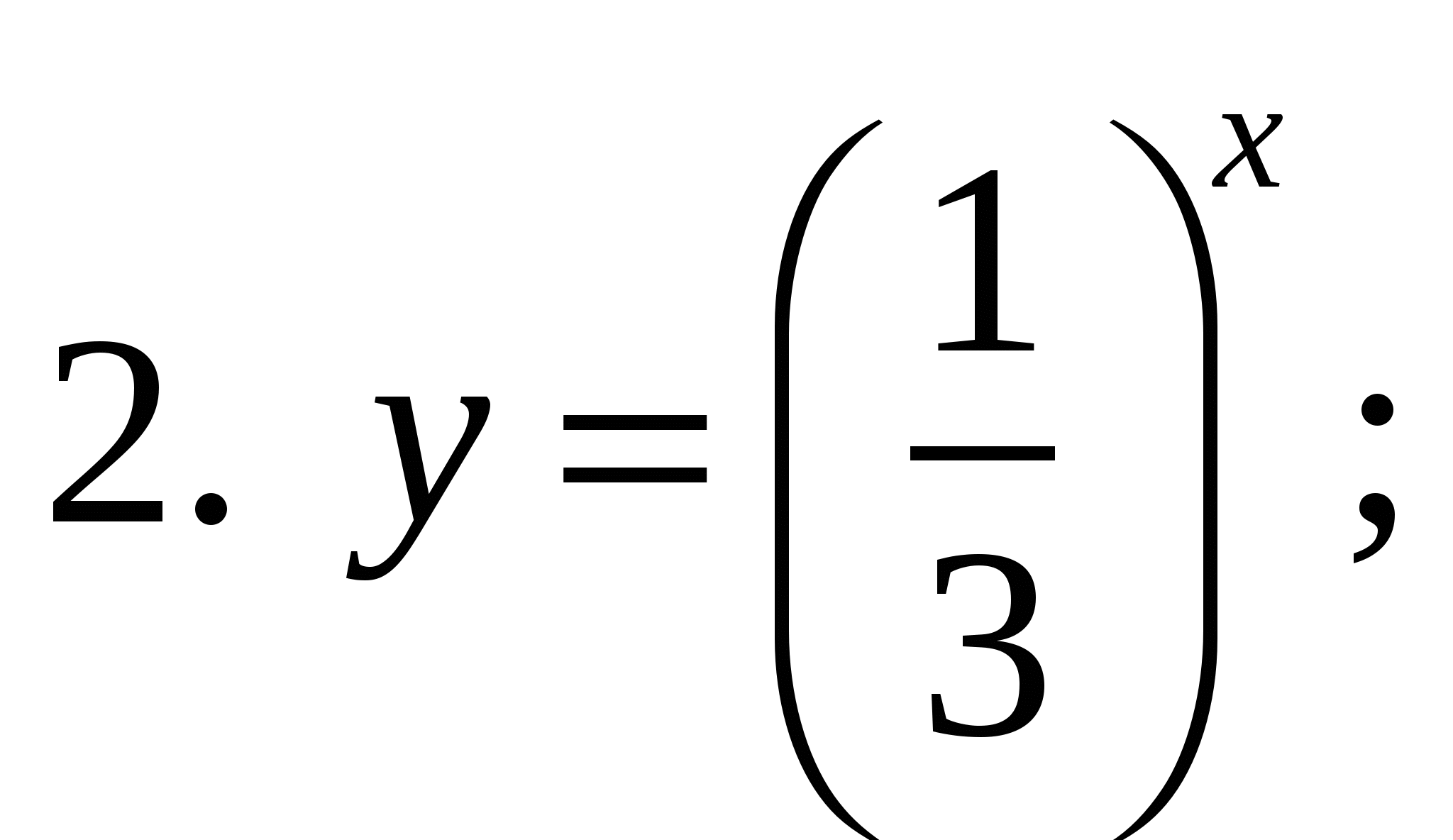
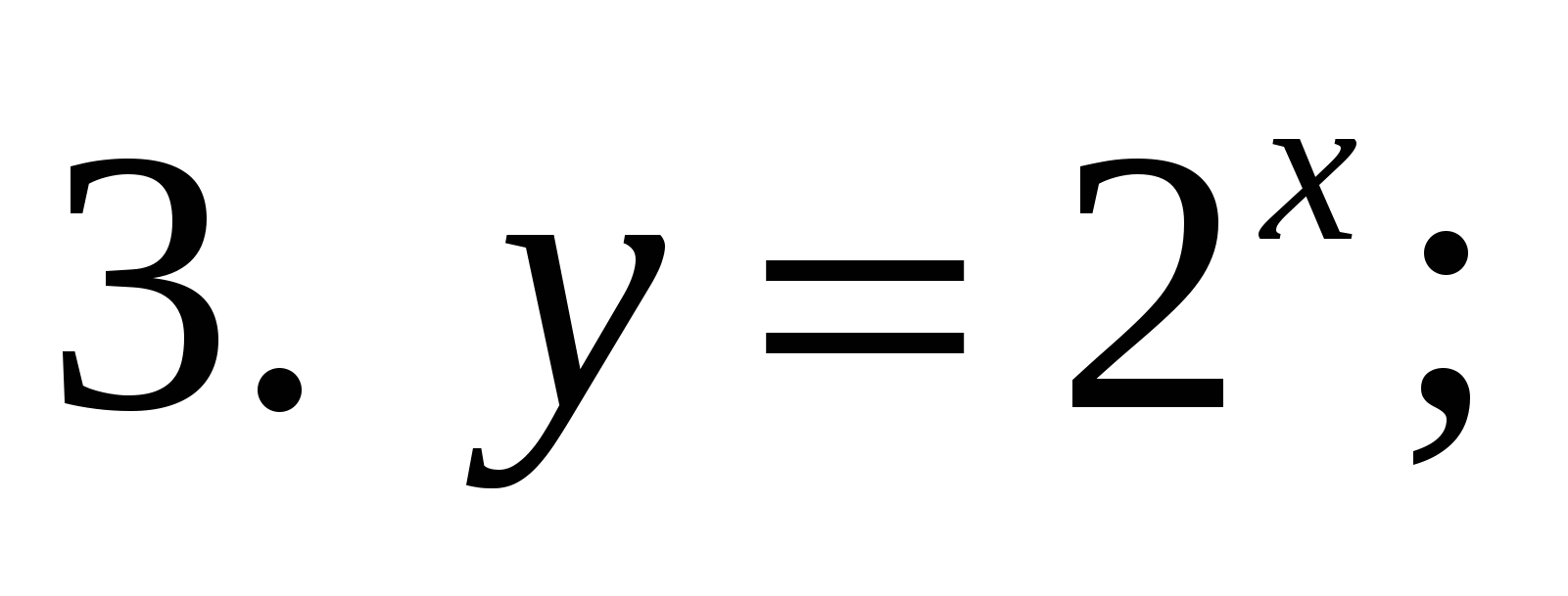
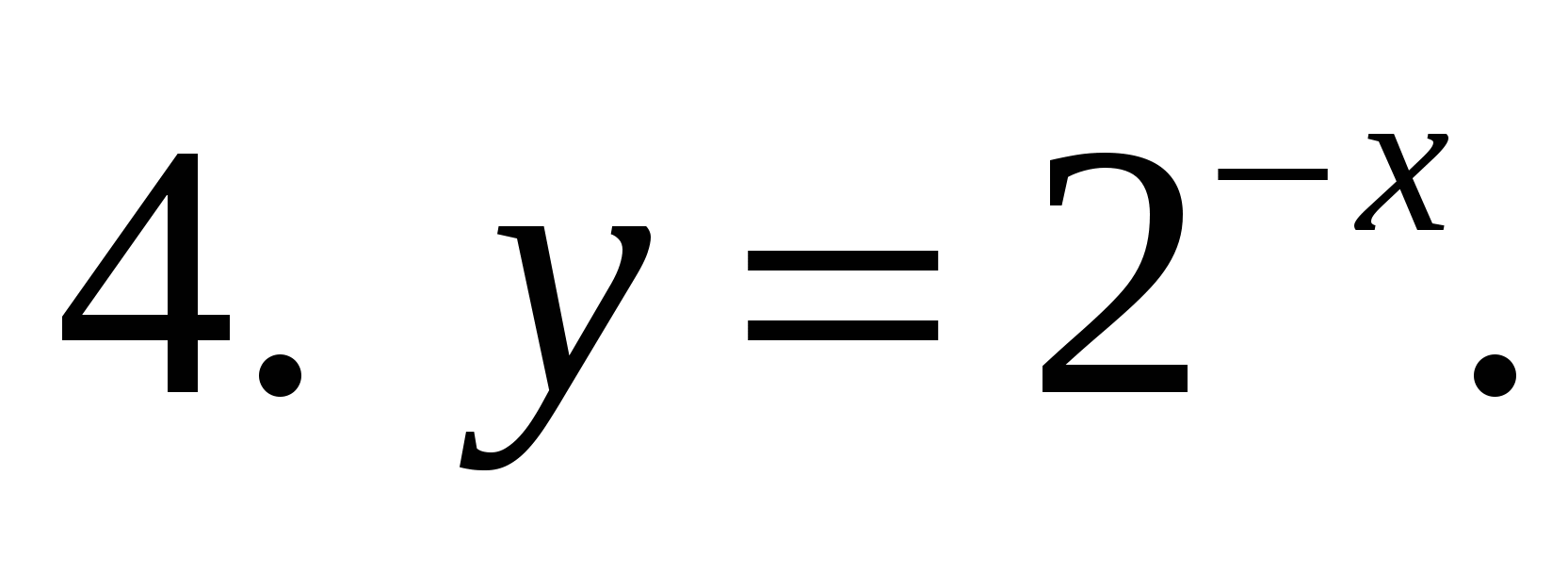
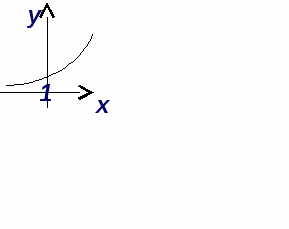
3. Укажите возрастающую функцию.
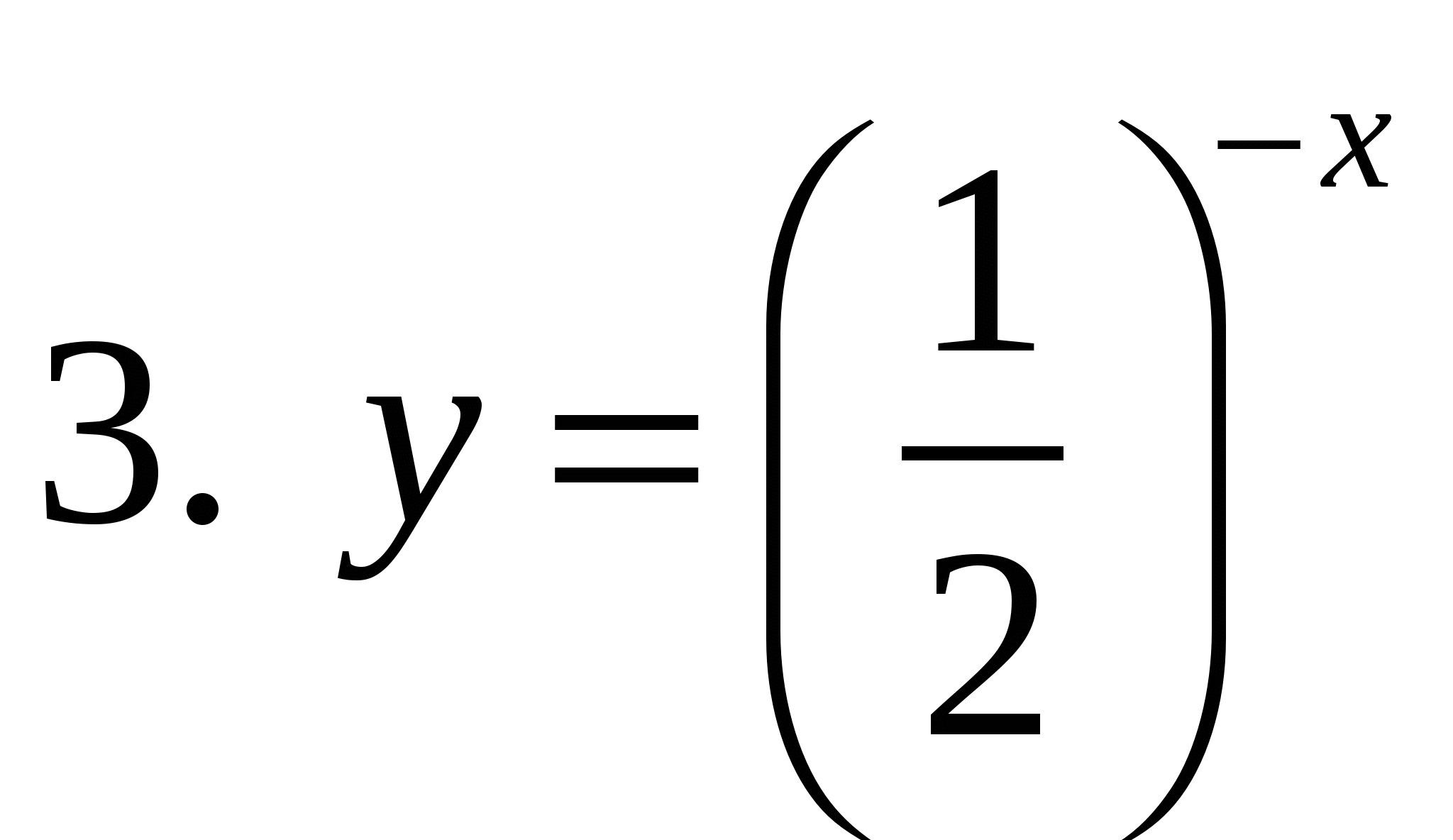
4. Укажите убывающую функцию.
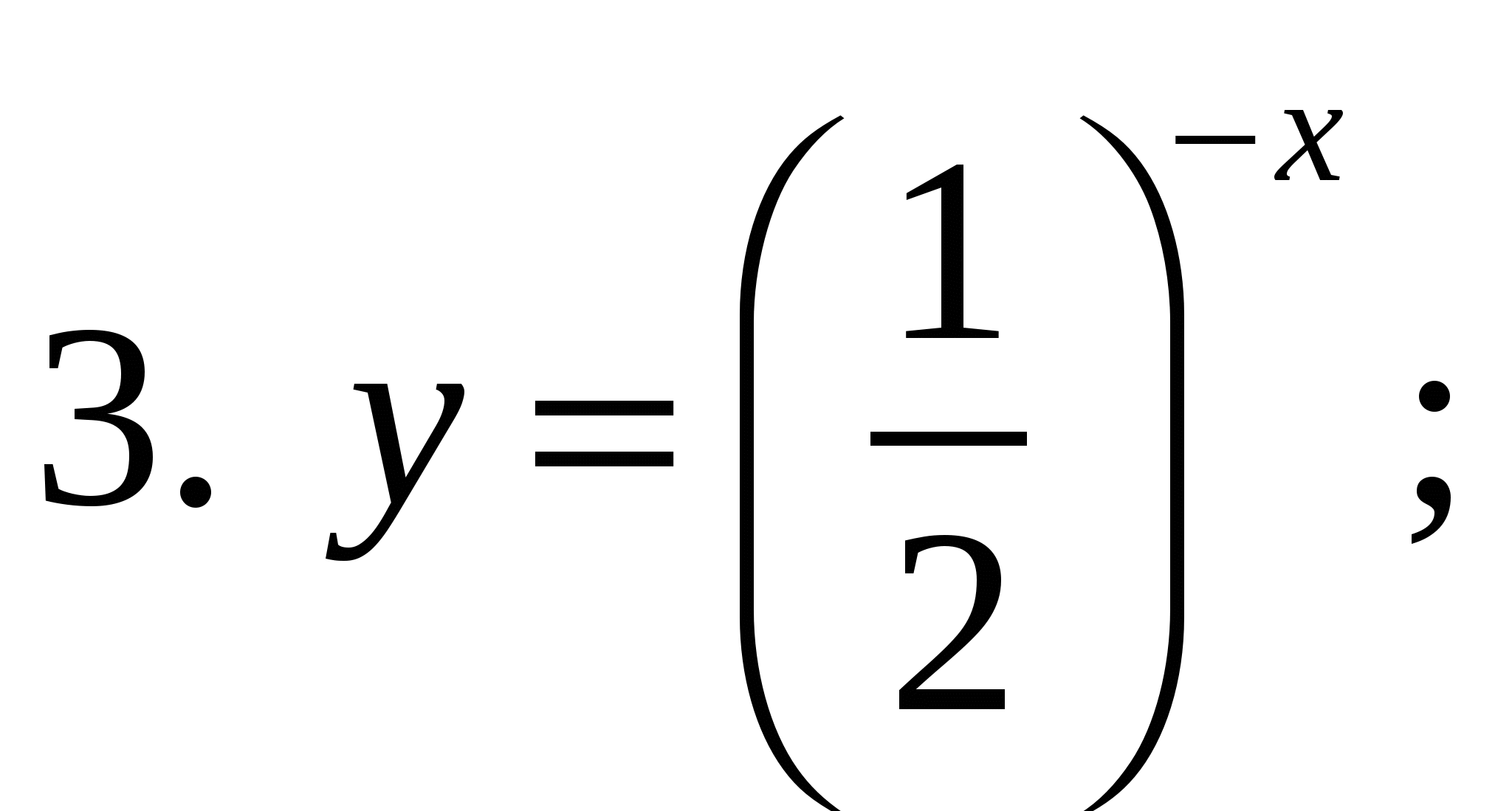
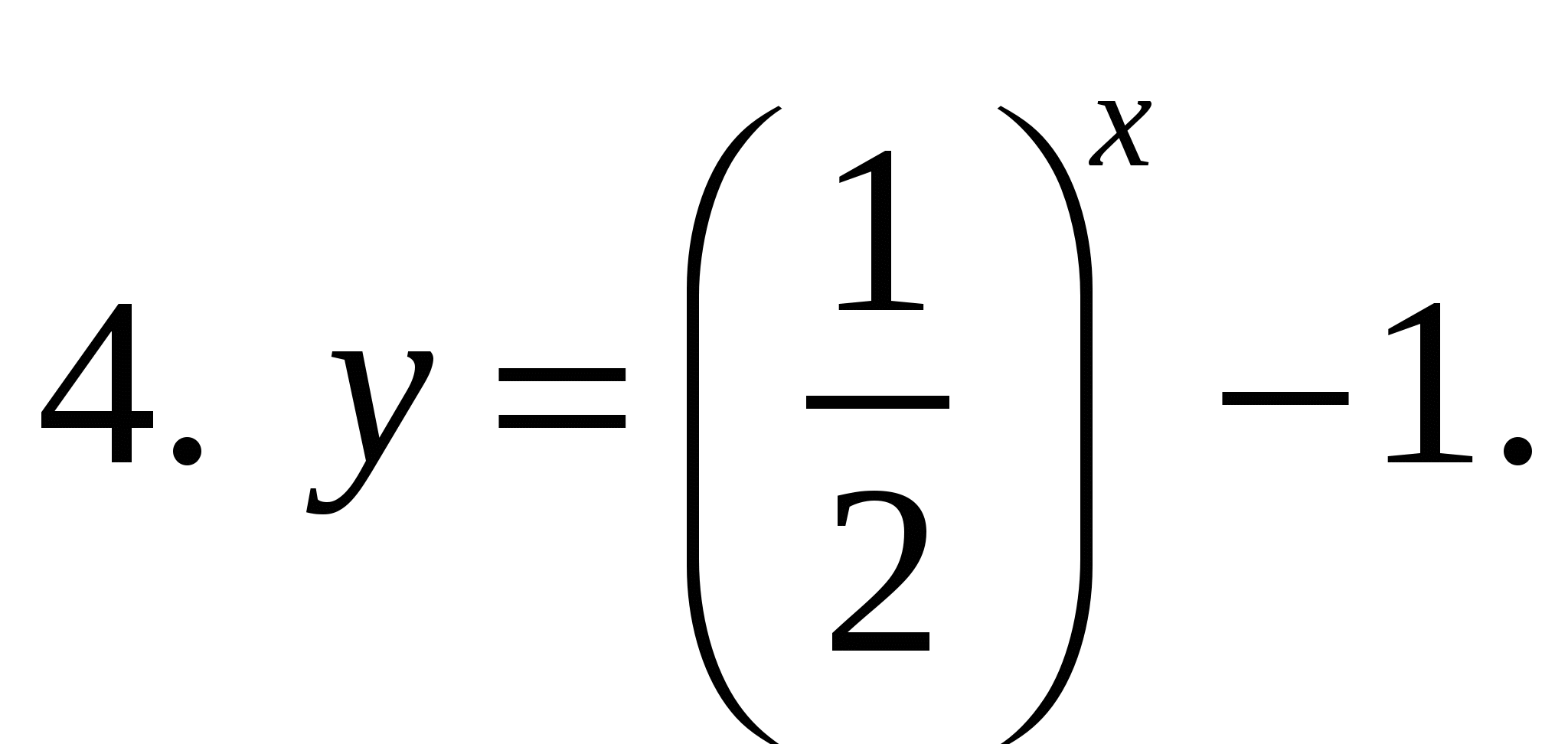
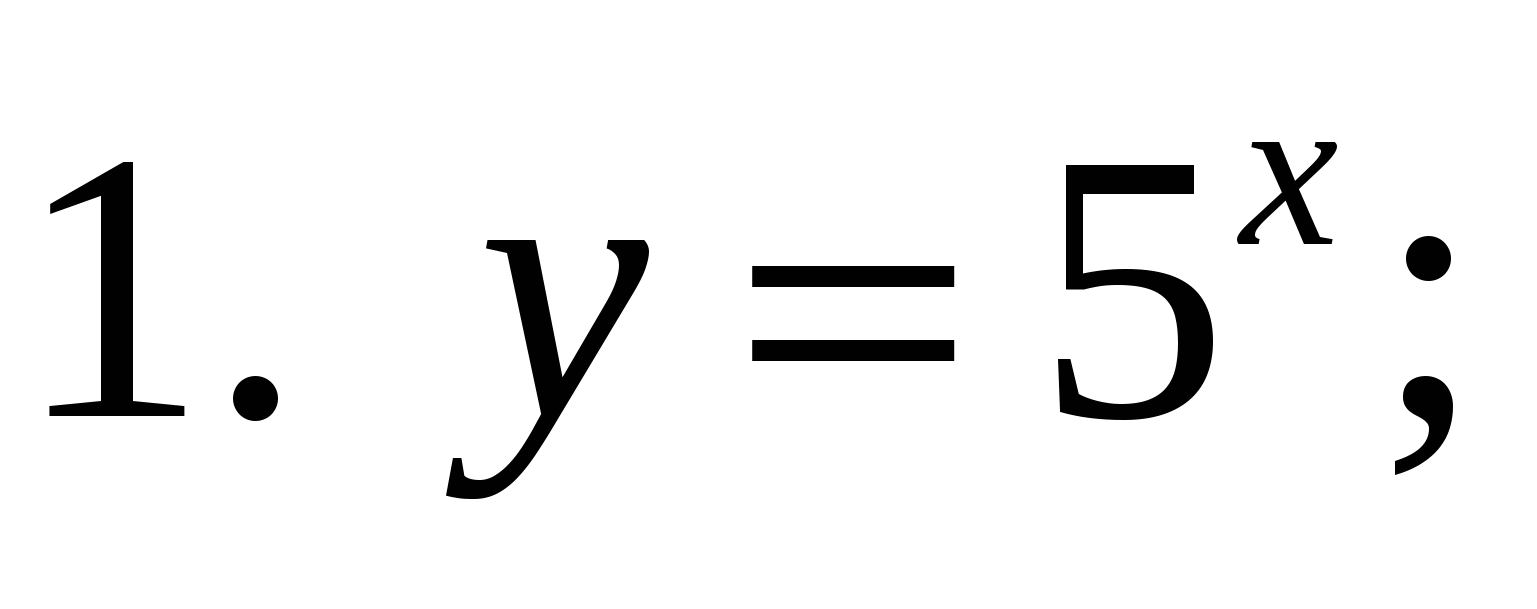
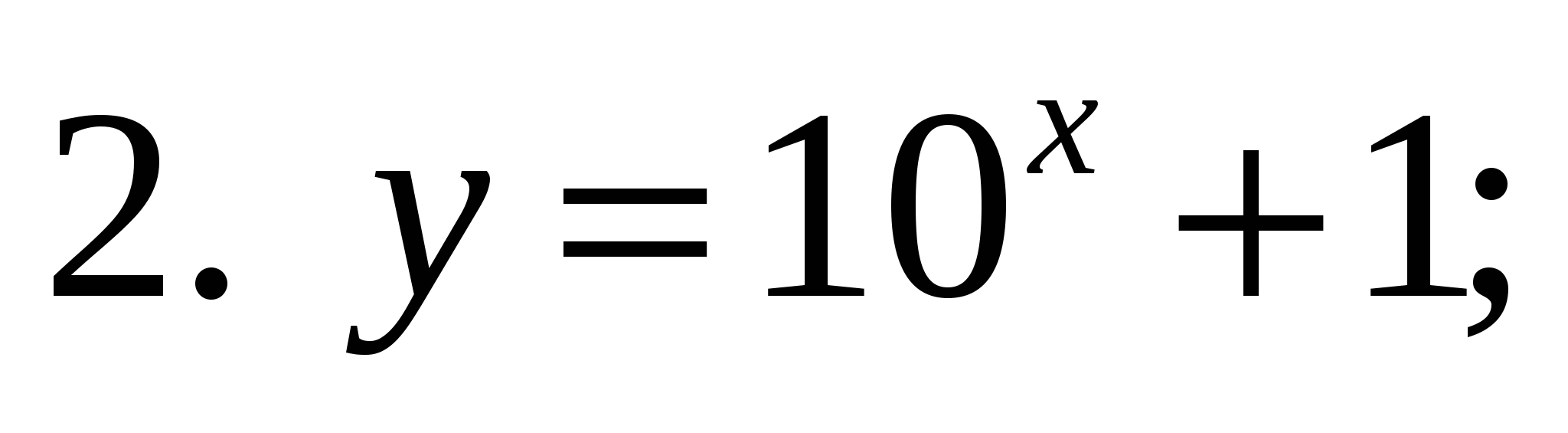
Письменно.
6. Найдите область значений функции у=4х-1. (слайды 17-18)
Область значений учащиеся находят с помощью преобразований графика функции. Все построения учащиеся выполняют в тетради.
(-1;+∞)
2 способ решения.
2х>0 для всех х,
2х-1>0-1
у>-1
(-1;+∞)
Формулирование правила.(слайды 19-20)
- Дана функция: у = ах ± b. Вывести правило, по которому можно,
не выполняя построение графика данной функции,
найти область значения функции.
Вывод:
Если у = а x + b, то Е (у) = (b; +∞)
Если у = а x -b, то Е (у) = (-b; +∞).
Устно выполнить задание на слайде 21. В тетрадь записать ответы. Затем выполнить самопроверку.
6. Подведение итогов. 3 минуты.
Выставление оценок.
Рефлексия учебного материала.
- С какой функцией познакомились на уроке?
- Дайте определение показательной функции.
- Вспомните свойства функции.
Рефлексия деятельности учащихся.
- Какой вид работы на уроке вам понравился? Почему?
- Какие трудности возникли?
7. Домашнее задание. ( слайд22) 1 минута.