Муниципальное бюджетное общеобразовательное учреждение
«Красноануйская основная общеобразовательная школа»
Солонешенского района Алтайского края
Конспект урока по математике в 7 классе«Умножение разности двух выражений на их сумму»
подготовила
учитель математики и информатики
Булгакова Ольга Алексеевна
с.Солонешное
2012
Цели урока:
Изучить формулу сокращенного умножения (а-b)(a+b)=a²-b²;
Научить применять её при умножении разности двух выражений на их сумму;
продолжить развитие мыслительных операций: наблюдения , сравнения, обобщения, конкретизации;
Продолжить развитие внимательности при изучении нового материала.
Тип урока: урок усвоения новых знаний
Методы: эвристическая беседа, репродуктивный метод.
Ход урока.
1.Организационный момент.
Приветствие детей.
2.Проверка домашнего задания
Двое детей из класса выполняют задания по карточкам, аналогичные домашнему заданию, а один ученик с обратной стороны доски.
Карточка
1.Представьте в виде квадрата двучлена выражение:
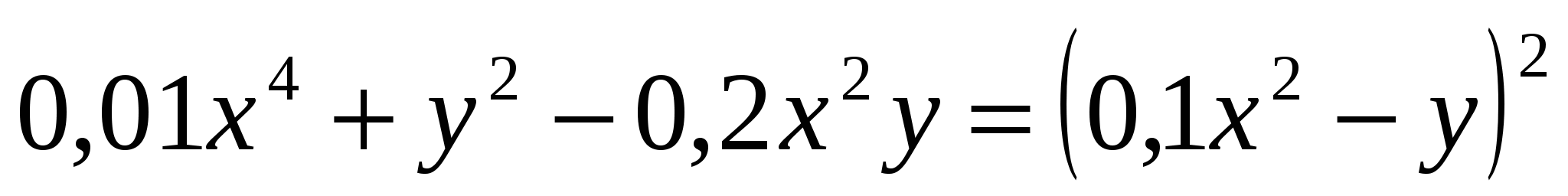
2) Заполните пропуски так, чтобы получились тождество:
(__+3b)²=__+54ab+__
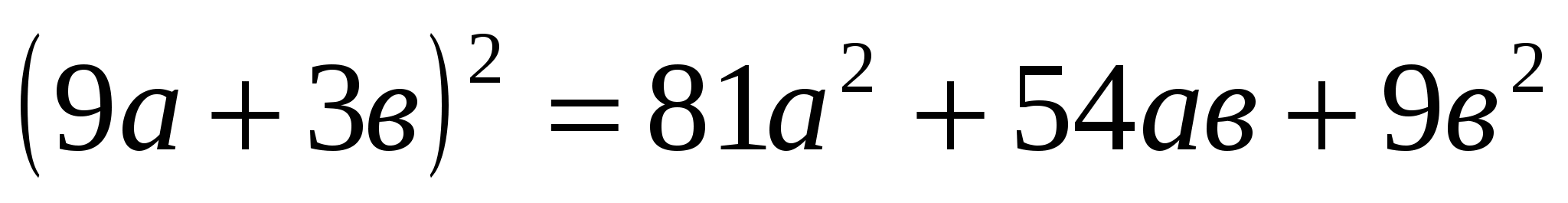
3) Разложите на множители: a³+a²b-2a-2b
a³+a²b-2a-2b=(a³+a²b)-(2a+2b)=a²(a+b)-2(a+b)=(a²-2)(a+b)
С остальными детьми устная работа.
3. Фронтальный опрос
а) Чему равен квадрат суммы двух выражений?
(Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого на второе выражение и плюс квадрат второго выражения)
б) Чему равен квадрат разности двух выражений?
(Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого на второе выражение и плюс квадрат второго выражения)
В) Чему равны выражения: (a+b)²; x²+2xy+y²; (a-b)²; m²-2mn+n²?
(a+b)²=a²+2ab+b²;
x²+2xy+y²=(x+y)²;
(a-b)²= a²-2ab+b²;
m²-2mn+n²=(m-n)²
Г) На доске записано задание. Представьте в виде квадрата двучлена выражения:
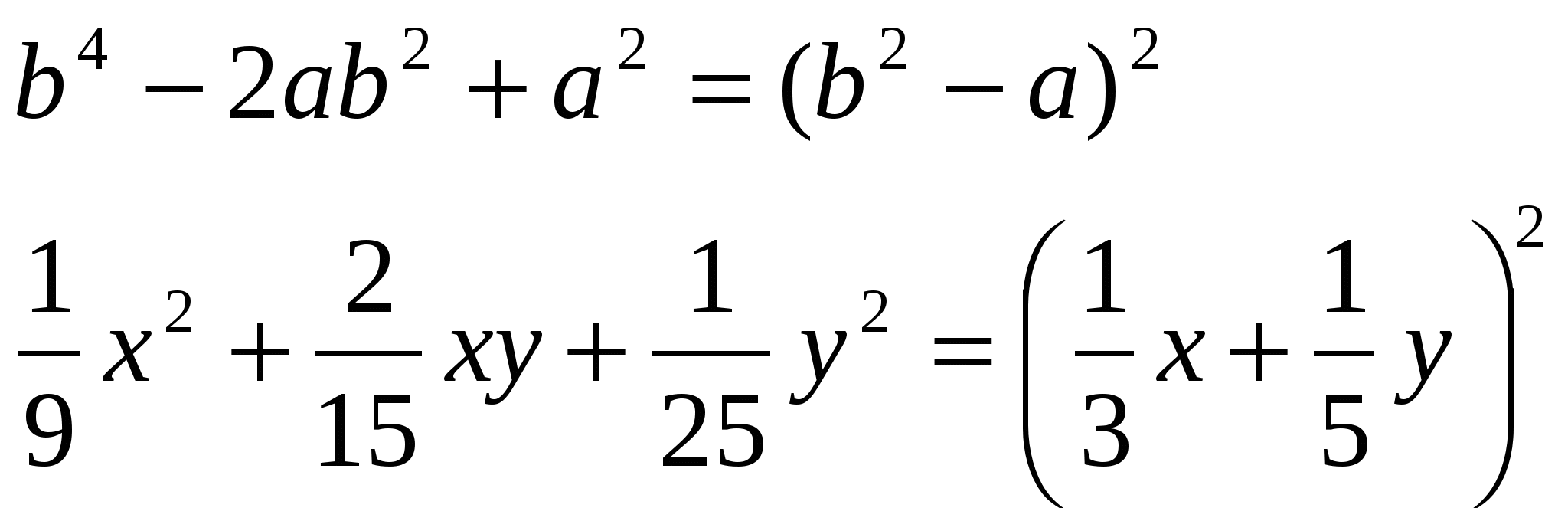
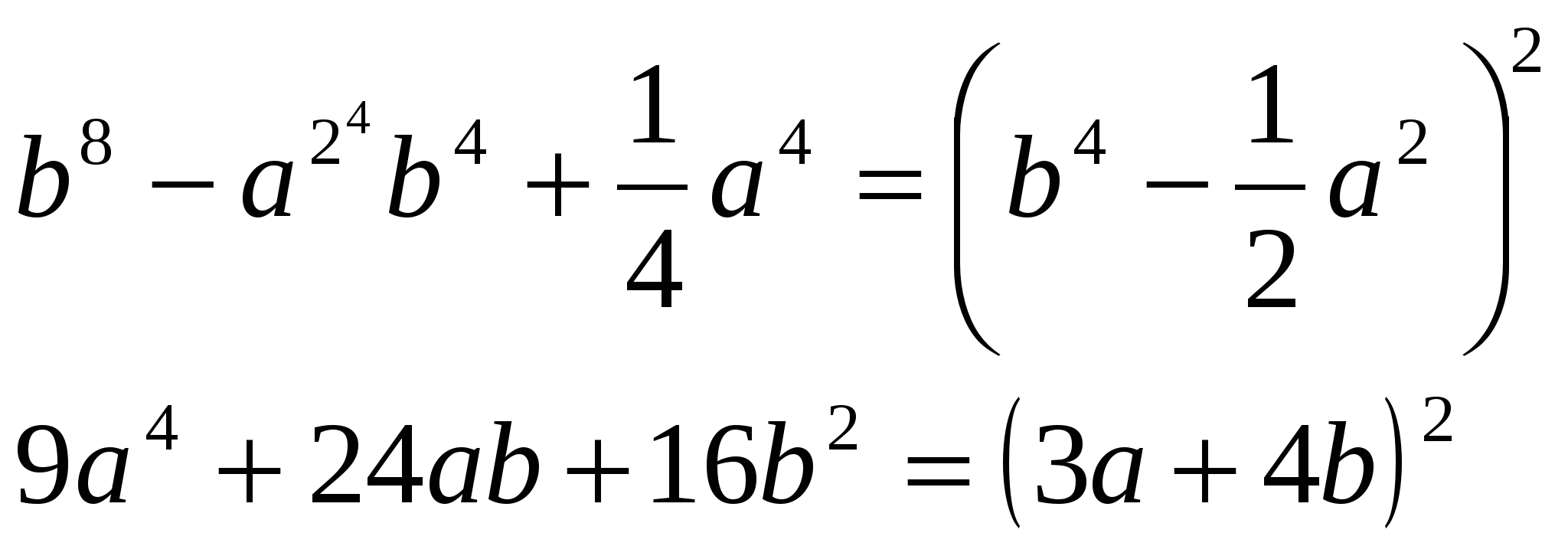
После работы устно, собрать карточки с решениями, проверить выполнение задания на доске с обратной стороны.
4. Изучение нового материала.
На доске и в тетради выполняется умножение:
(c-d)(c+d)=c²+cd-dc-d²=c²-d²
(m-n)(m+n)=m²+mn-nm-n²=m²-n²
(x-y)(x+y)=x²+xy-yx-y²=x²-y²
Дети замечают, что при умножении разности и суммы двух выражений справа всегда получается разность квадратов первого и второго выражения.
Вместе с детьми формулируется правило умножения разности двух выражений на их сумму.
(Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.)
(а-b)(a+b)=a²-b².
Это правило и формула на таблице раскладушке прикрепляется к доске.
5.Закрепление изученного материала.
Детям предлагается по формуле выполнить:
(р-q)(p+q)=p²-q².
(3x-1)(3x+1)=9x²-1Работа по учебнику:
№915(в,д,ж,и)
в) 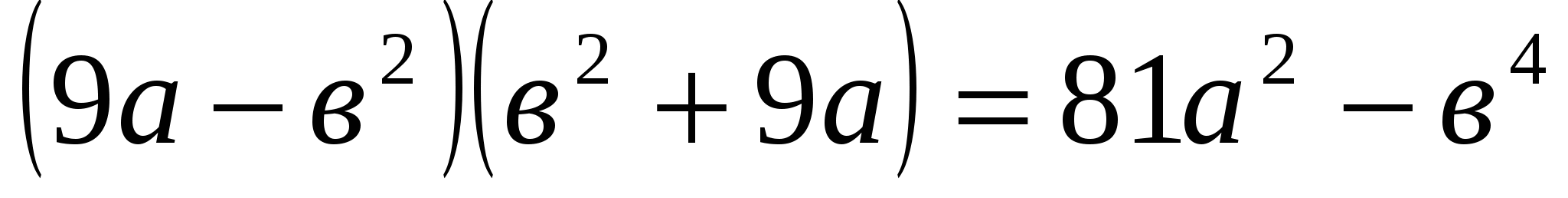
д)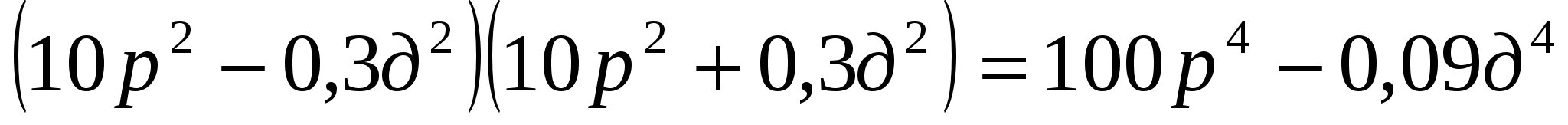
ж)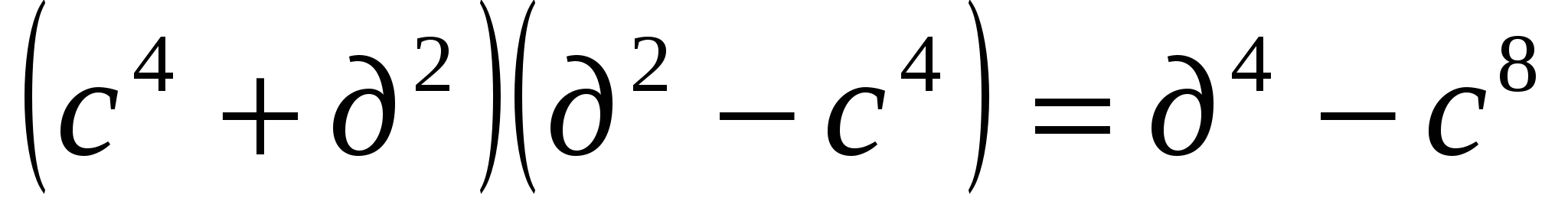
и)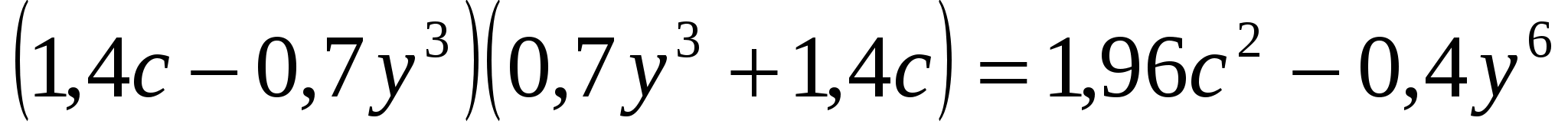
№917(в,д)
в)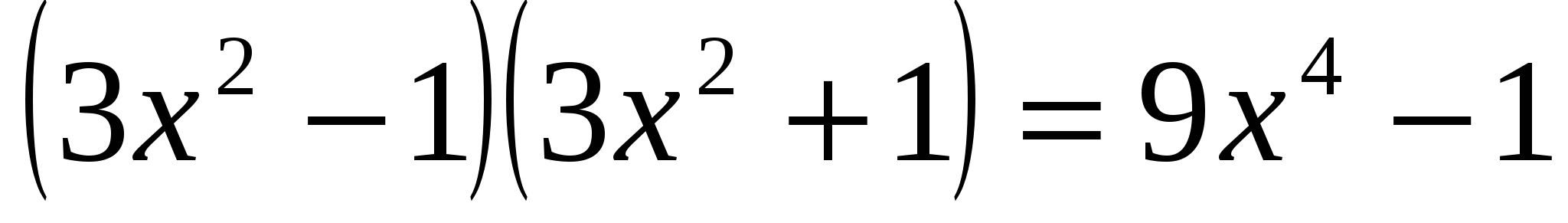
д)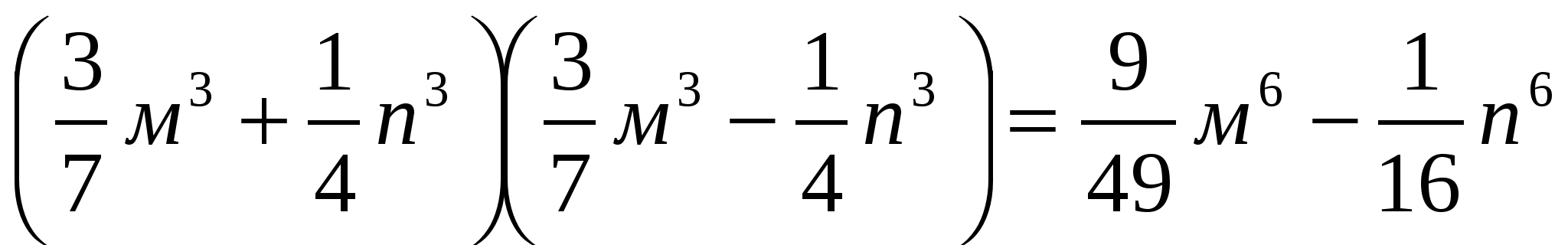
6.Итог урока
1.Чему равно произведение разности двух выражений и их суммы?
(Произведение разности двух выражений и их суммы равно разности квадратов этих выражений)
На доске записаны задания:
2.Заполните пропуски:
а) (__-3x)(__+3x)=16y²-9x²
б) a-144b=(a²-__)(a²+__)
Ответы:
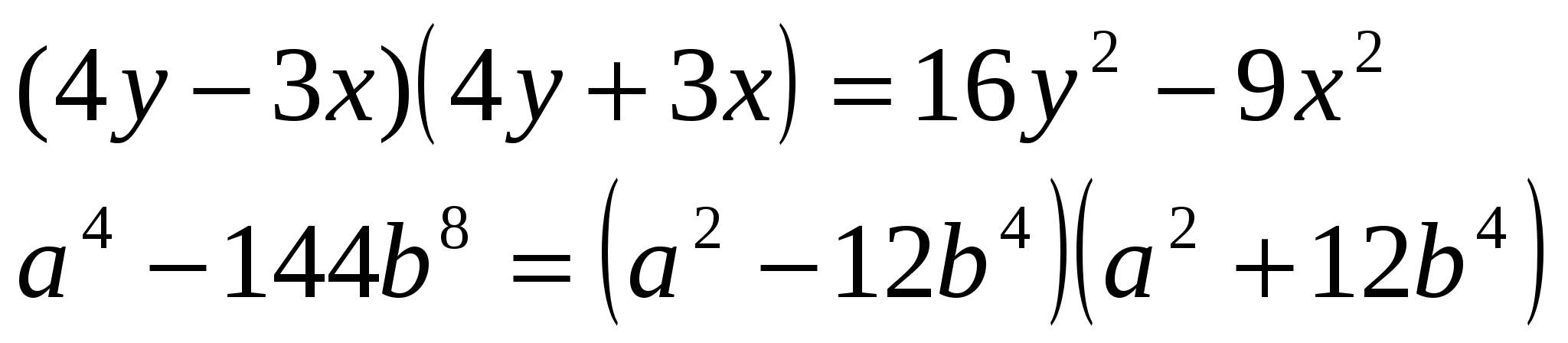
3.Найдите ошибку:
a) 2(x-3)(x+3)=2(9-x²). {2(x-3)(x+3)=2(x²-9)}
б)(5а-4b)(5a+4b)=5a²-4b². {(5а-4b)(5a+4b)=25a²-16b².}
Выставление оценок за урок.
7.Домашнее задание.
§13,п.33, №915(б,д,е,з), №916(а,в,д), № 917(б,г)
Список использованной литературы:
Макарычев Ю.Н. и др.Алгебра.7 класс.- М.: «Просвещение», 2005.
Поурочные планы по учебнику Макарычева Ю.Н и др. Алгебра.7 класс, - Волгоград: «Учитель», 2003.