Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 17 села Краснопартизанского
Урок разноуровневого обобщающего повторения
по теме «Решение дробных рациональных уравнений »
по алгебре
для учащихся 8 класса
Автор разработки Титенко Ольга Григорьевна
С.Краснопартизанское
2012 год
Длительность урока 40 мин. Тема урока выбрана на основании анализа результатов предыдущей краевой контрольной работы в данном классе, которая выявила, что учащиеся класса не в полной мере усвоили тему : « Решение дробных рациональных уравнений». В классе 8 учеников. По результатам диагностической работы выявлено, что только 57 % учащихся справились с заданием по данной теме, при планируемой трудности 89 %.
Перед началом урока учащиеся рассаживаются в соответствии с тремя уровнями подготовки на определенные учителем места ( ряды) для удобства организации работы. При этом учащиеся знают, что по мере усвоения материала или отставания, они могут переходить в другую по уровню подготовки группу.
Цели урока: - обобщить теоретические знания по теме: «Решение дробных рациональных уравнений»,
- применять теоретические знания для решения уравнений базового и повышенного уровня сложности,
- организовать работу учащихся по указанным темам на уровне, соответствующем уровню уже сформированных у них знаний.
Оборудование: 1. Мультимедийная установка. На уроке используется презентация-алгоритм решения дробных рациональных уравнений, презентация – ответы к решенным уравнениям.
2.Раздаточный материал, подготовленный учителем для организации самостоятельной работы. Для каждой группы учащихся используются задания, напечатанные на карточках различных цветов: для первой группы- зеленые; для второй – голубые; для третьей - розовые
1 этап урока – Организационный ( 1 минута).
Учитель сообщает учащимся тему урока, цель и поясняет, что во время урока постепенно будет использоваться тот раздаточный материал, который находиться у них на партах.
2 этап урока – Повторение теоретического материала по теме ( 7минут).
Учитель: Какие уравнения называются рациональными уравнениями?
Ученик: Уравнения называются рациональными, если его левая и правая части являются рациональными выражениями.
Учитель: Какие рациональные уравнения называются дробными?
Ученик: Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называют дробным.
Учитель вызывает к доске хорошо подготовленного учащегося и на конкретном примере напоминает алгоритм решения дробных рациональных уравнений. ( Пример 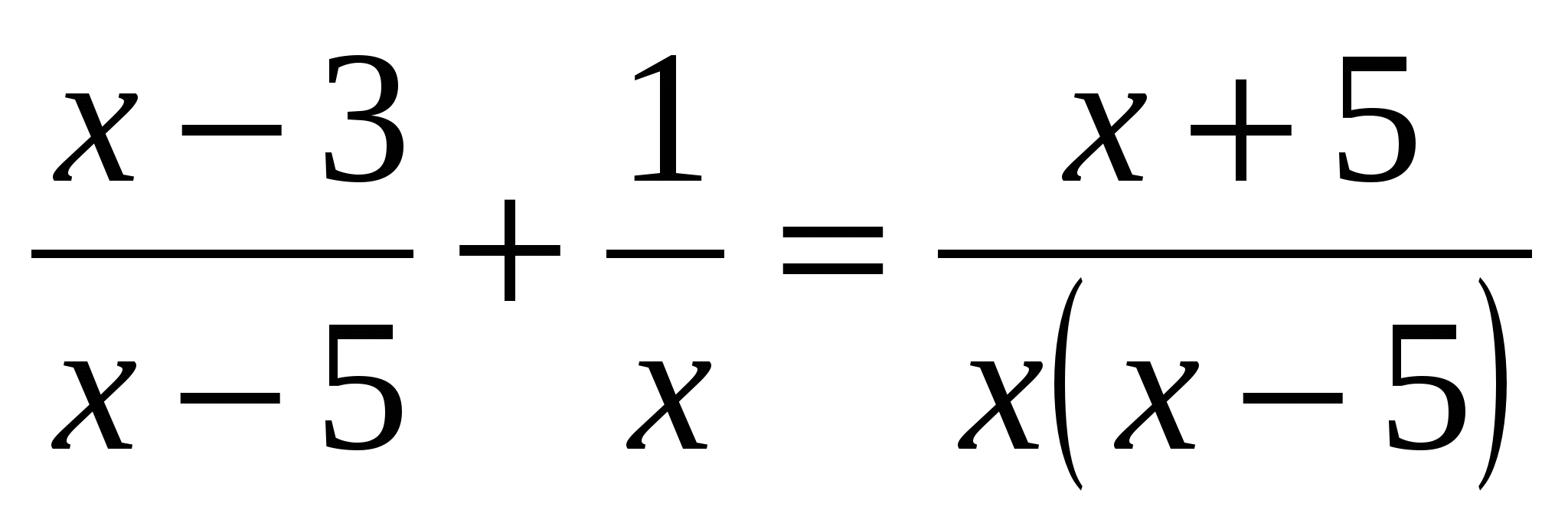 )
)
Учитель. Давайте сформулируем алгоритм решения дробных рациональных уравнений.
Ученик: Чтобы решить дробные рациональные уравнения нужно:
Найти общий знаменатель дробей, входящих в уравнение.
Умножить обе части уравнения на общий знаменатель.
Решить получившееся целое уравнение.
Исключить из его корней те, которые обращают в нуль общий знаменатель.
( На экране мультимедийной системы учитель демонстрирует алгоритм решения уравнений).
3 этап урока – Устная работа по решению задач на изучаемую тему
( 5 мин.)
Назовите общий знаменатель в уравнениях.
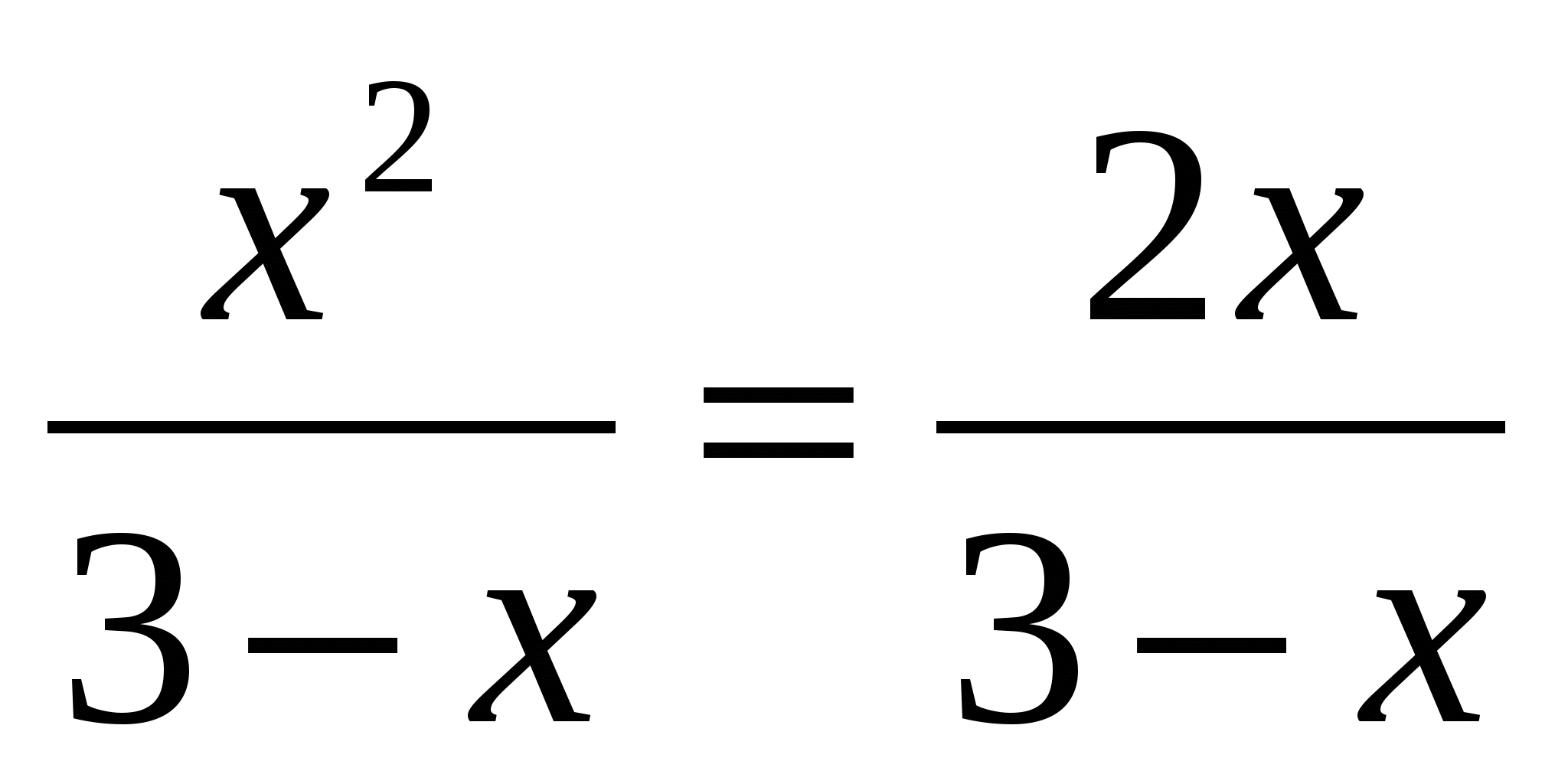
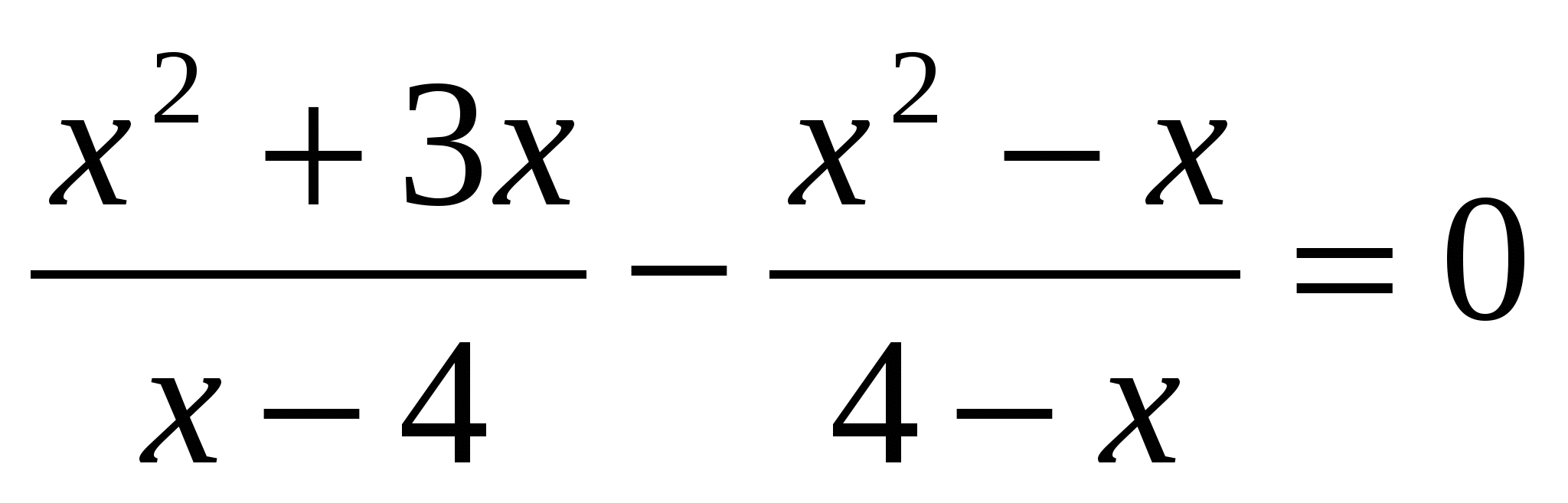
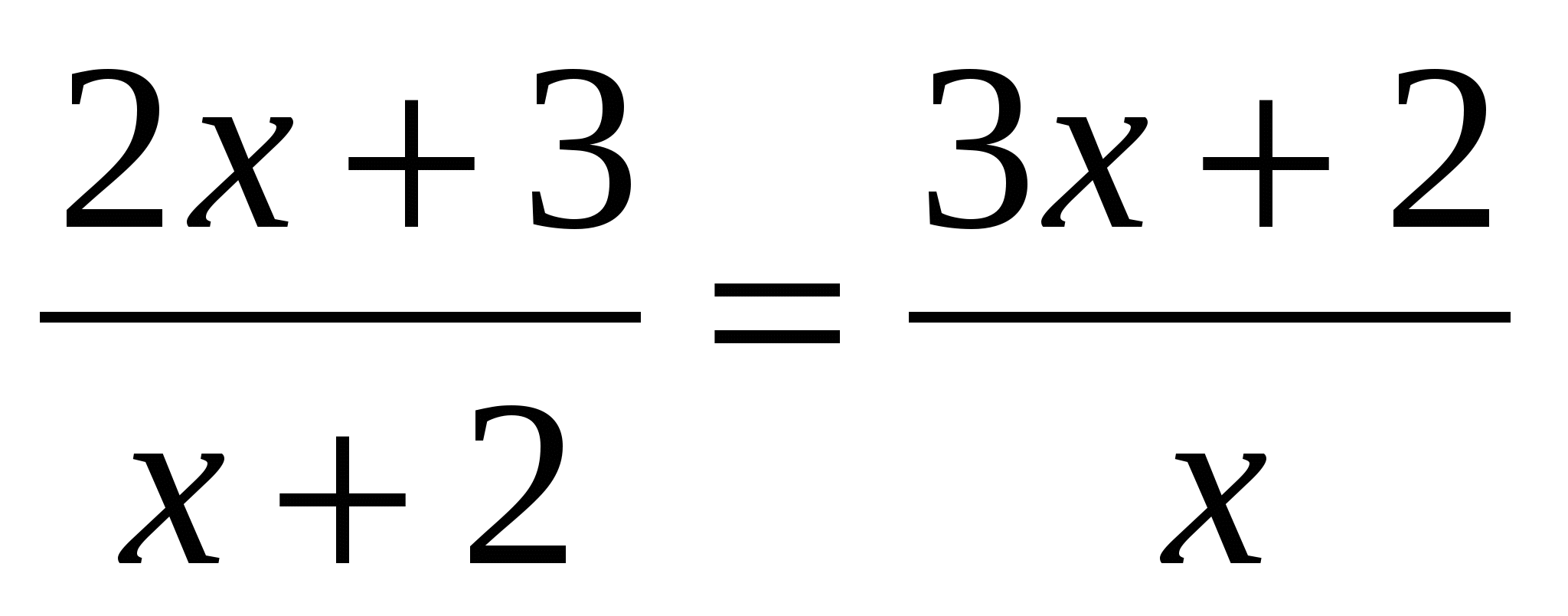
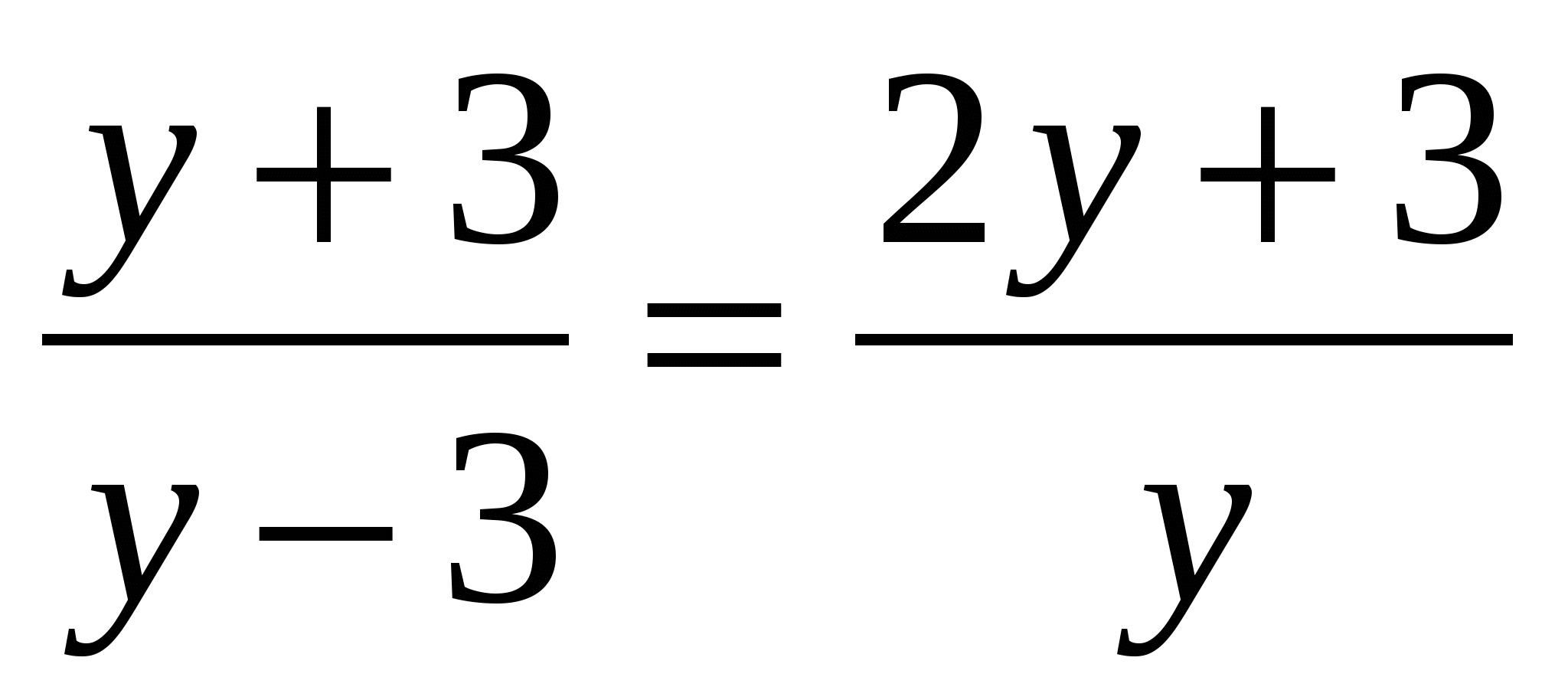
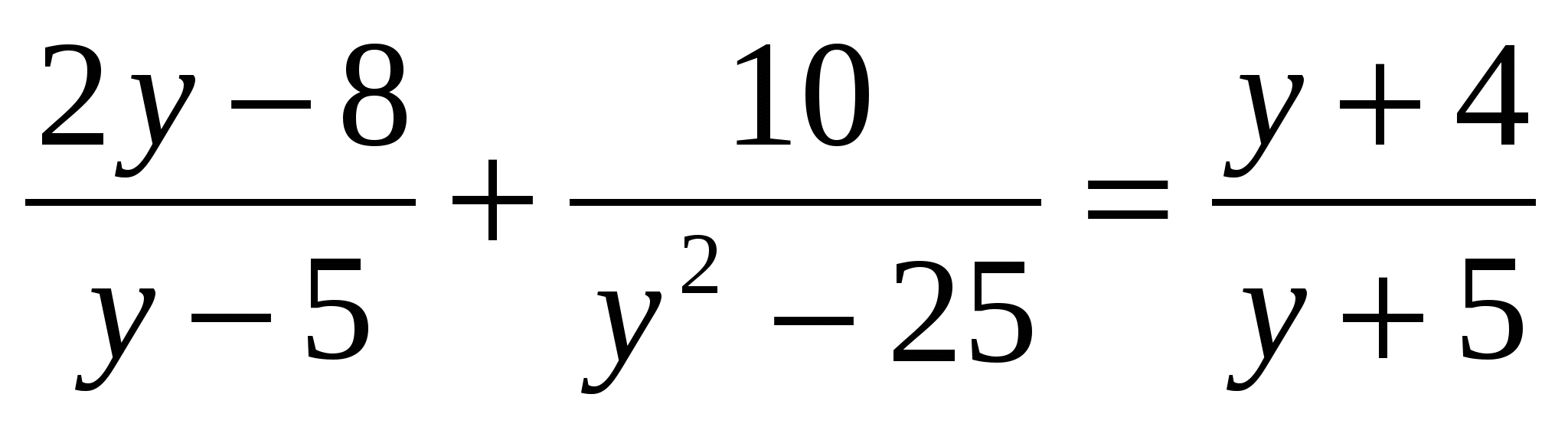
Какие числа обращают в нуль общий знаменатель уравнений?
4 этап урока – Работа в разноуровневых группах ( 10 мин)
Со всеми учащимися класса рассматриваются решения уравнений у доски. Учащиеся выходят к доске и решают с объяснением уравнения, причем учитель вызывает работать сильных учеников, чтобы они объясняли слабым решение уравнений.
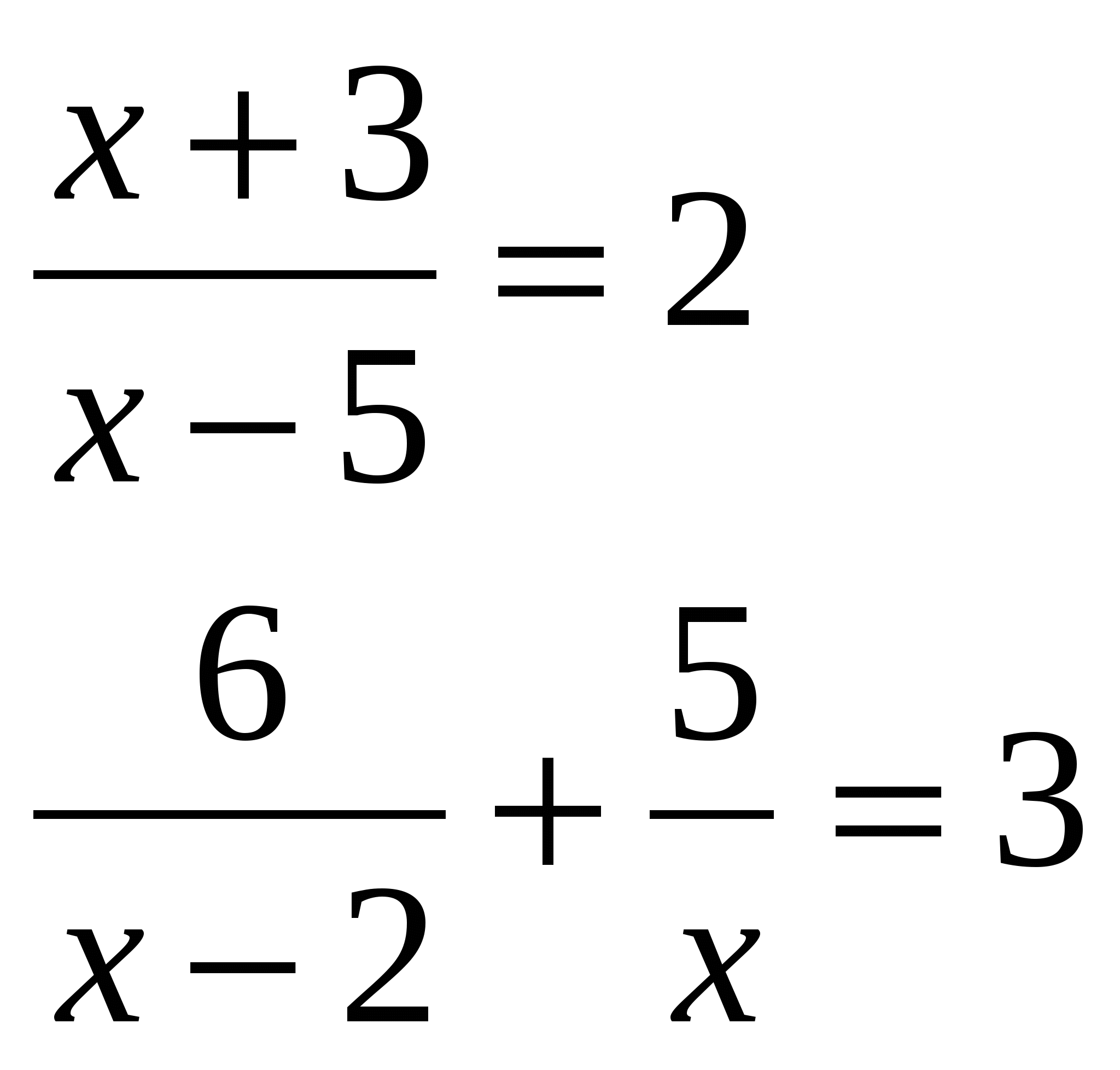
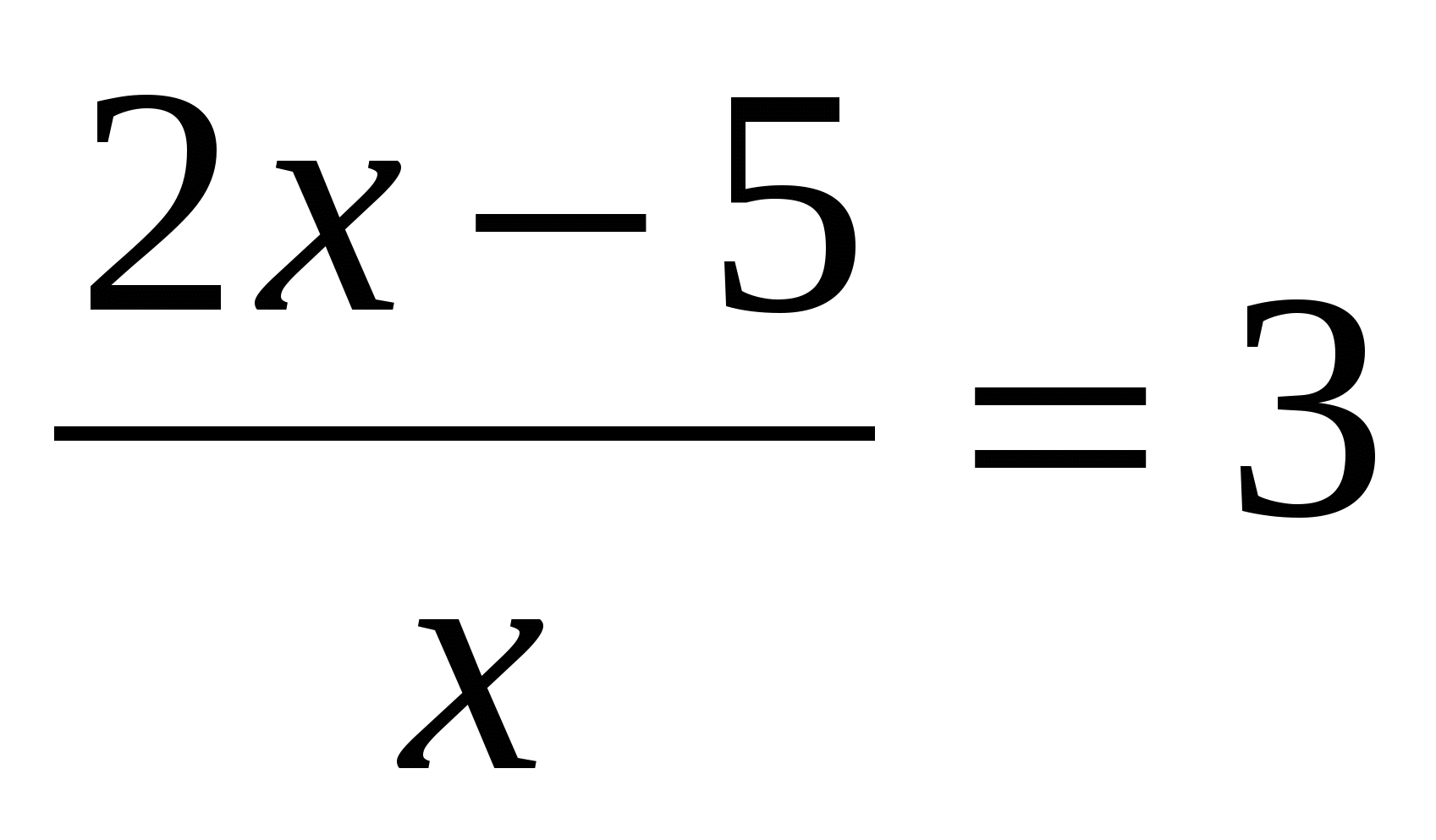
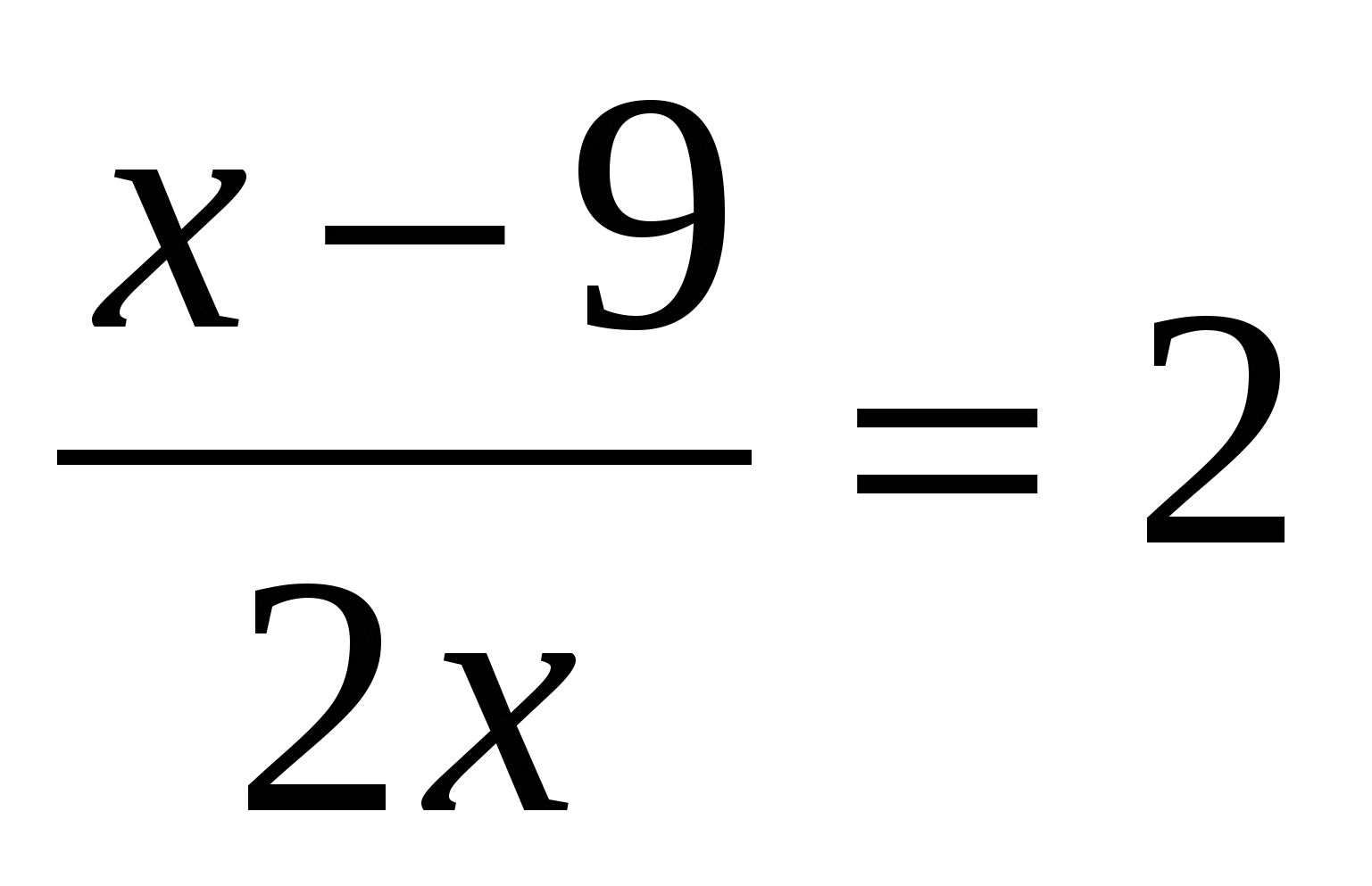
Далее первая группа учащихся самостоятельно выполняет задания аналогичные тем, которые будут представлены в зеленой карточке самостоятельной работы, а в это время учитель с учащимися второй и третьей группы рассматривает задания повышенного уровня сложности.
Задания для второй и третьей группы.
Решить уравнение.
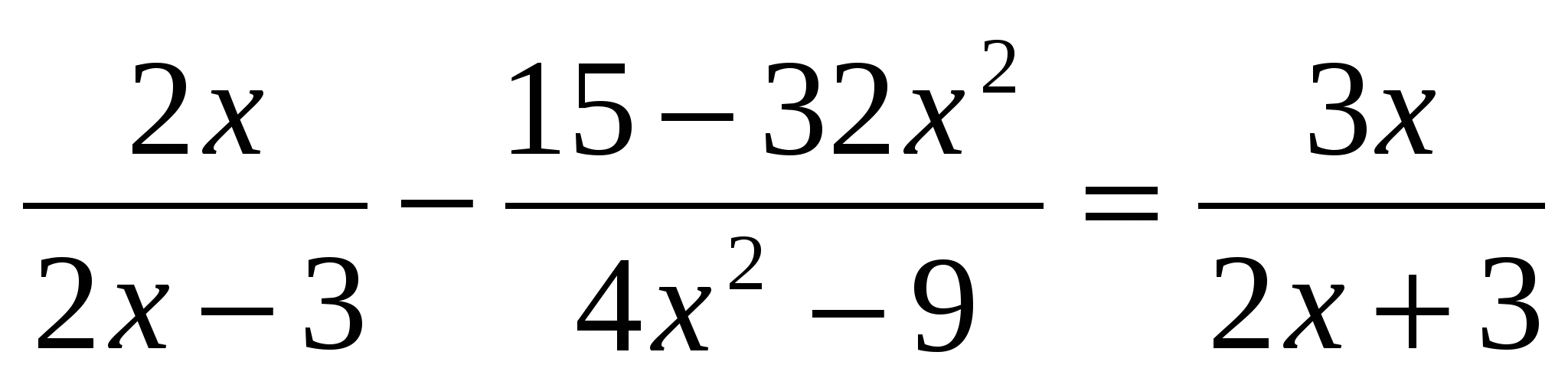 ( Ответ: -1;
( Ответ: -1;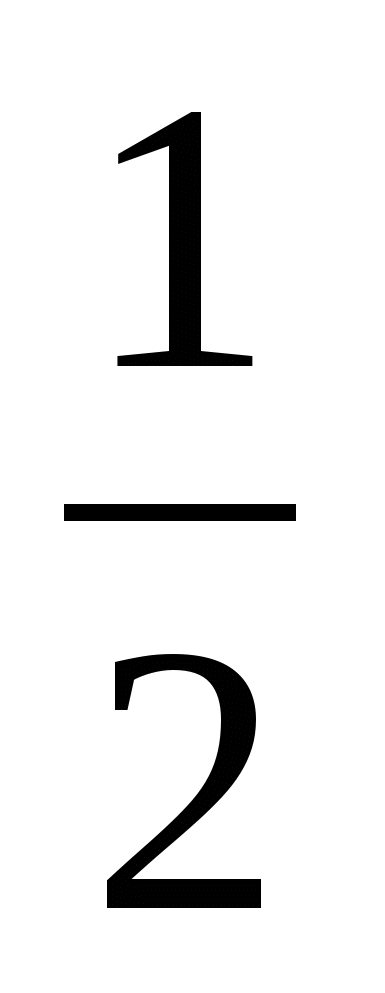 )
)
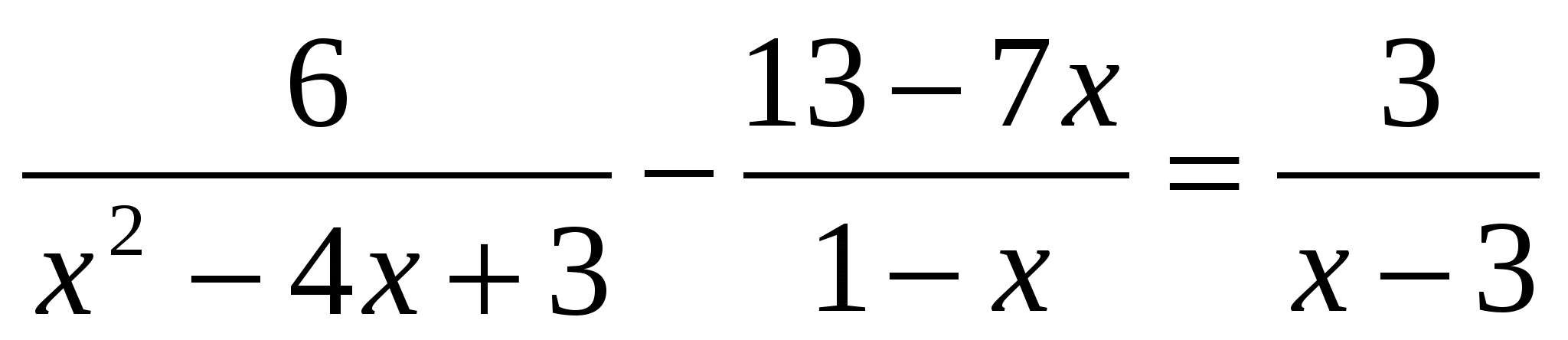 ( Ответ:
( Ответ: 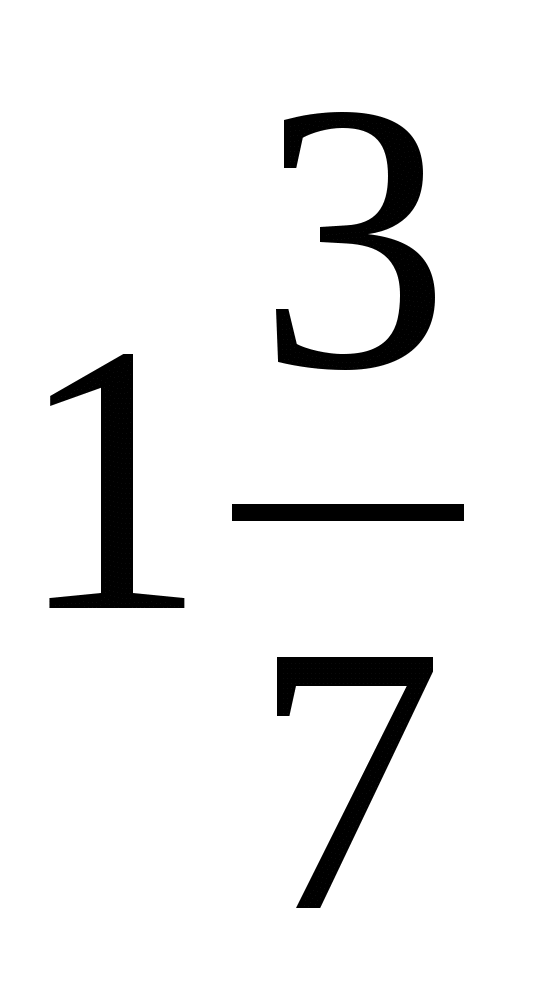 )
)
Задания для учащихся работающих самостоятельно: ( аналогичные заданиям в зеленой карточке, имеется в ввиду такого же уровня сложности).
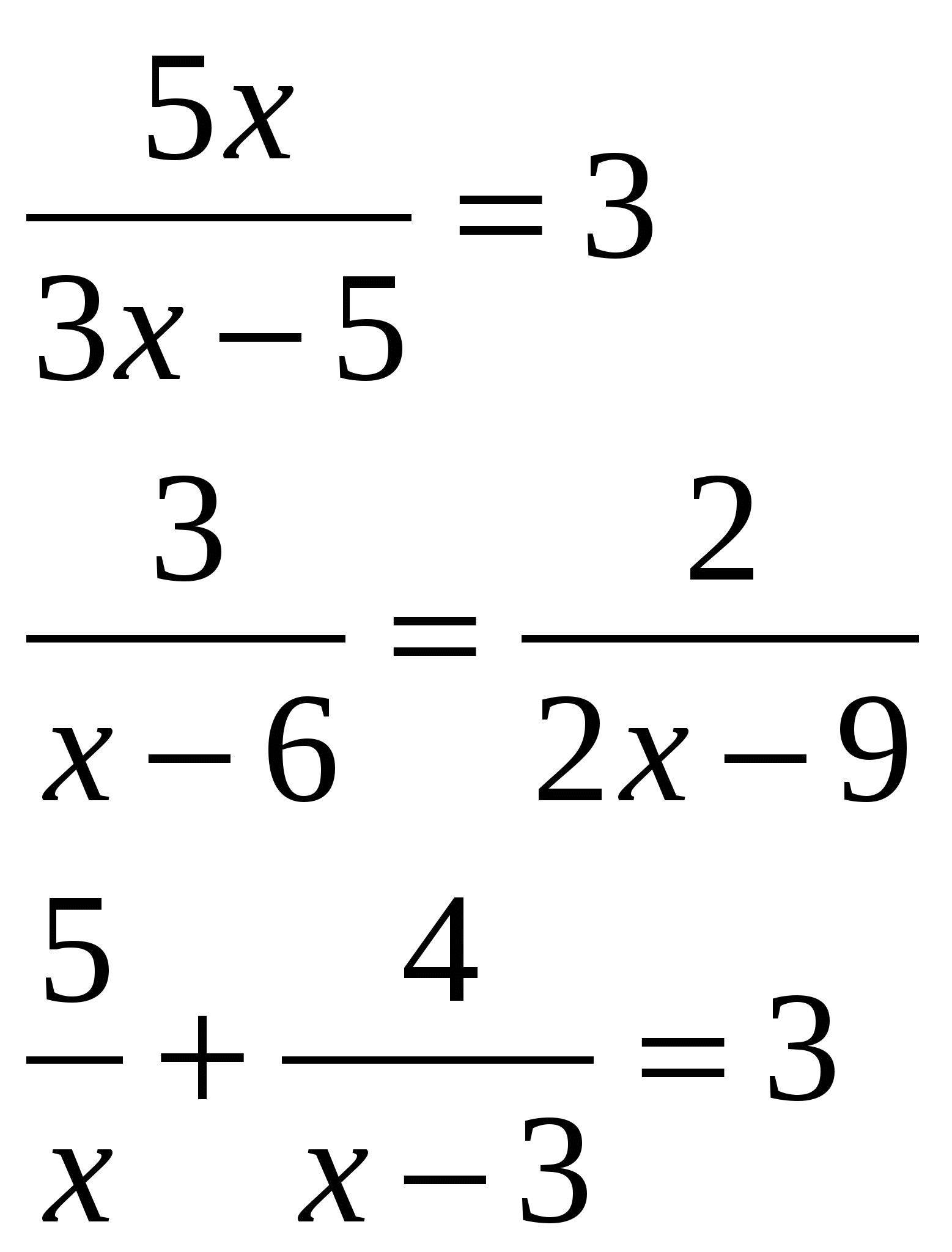
Далее, вторая и третья группы работают самостоятельно, выполняя задания, аналогичные тем, которые будут в самостоятельной работе в голубой и розовой карточке.
Пока они работают, учитель проверяет решения уравнений учащихся первой группы, комментируя их при необходимости. После чего проверяются ответы у учащихся второй и третьей группы. Ответы учитель показывает на слайдах и учащиеся проверяют правильность выполнения заданий.
Задания для учащихся второй группы.
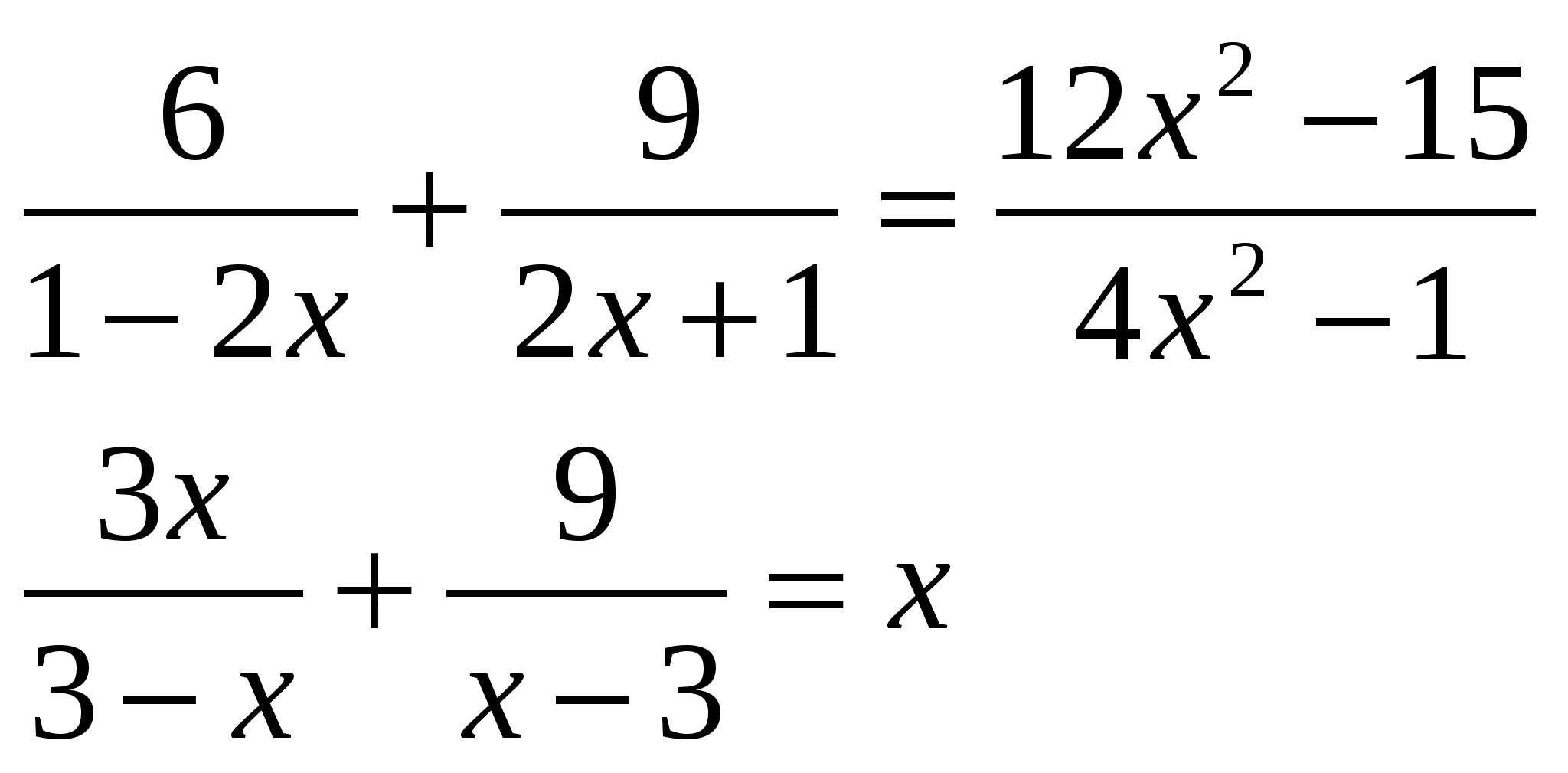
Задания для учащихся третьей группы.
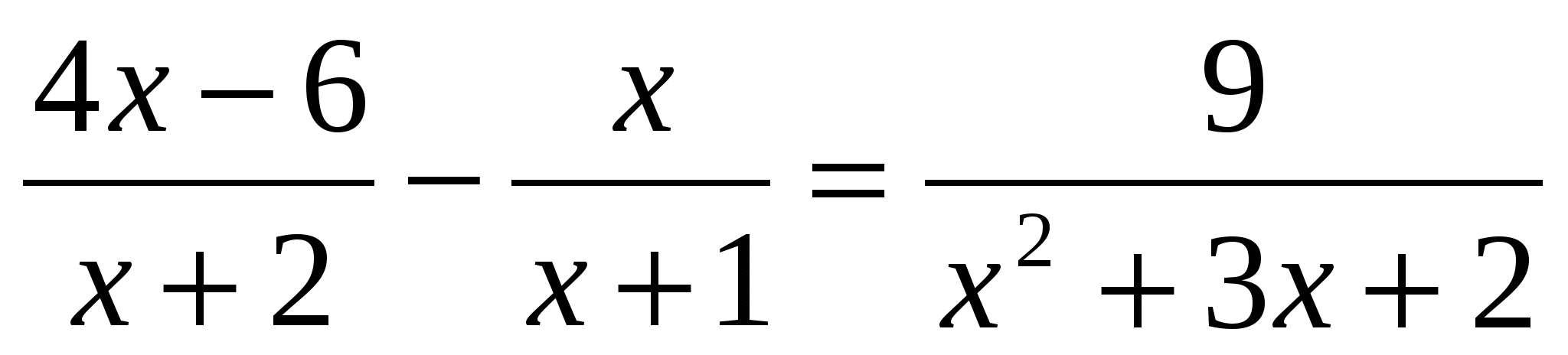
5 этап урока – Разноуровневая самостоятельная работа ( 15 минут).
Учитель сообщает, что на самостоятельную работу отводится 15 минут. Учителем подготовлены карточки трех цветов для удобства ориентации по уровням сложности.
Для учащихся первой группы учителем составлены зеленые карточки с заданиями базового уровня сложности. Учащиеся первой группы - это, как правило, учащиеся со слабой математической подготовкой , педагогически запущенные школьники, они будут выполнять задания под контролем учителя.
Для учащихся второй группы учитель выдал голубые карточки с разнообразными заданиями базового уровня сложности.
Для учащихся третьей группы учитель выдал розовые карточки с заданиями повышенного уровня сложности.
Все варианты содержат два вычислительных задания и три задания на рассмотренную на уроке тему.
Зеленая карточка.
Вычислите
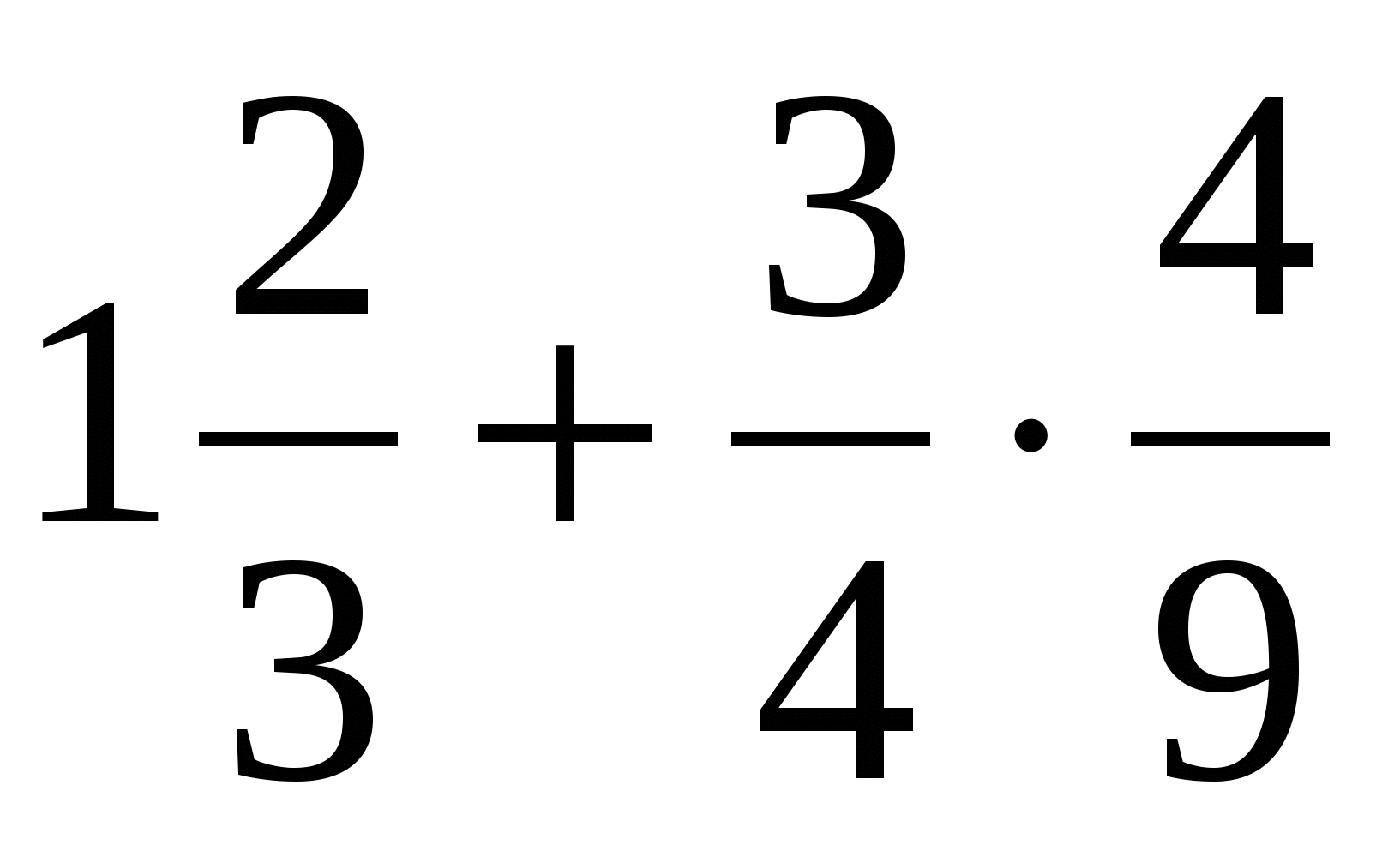
1) 1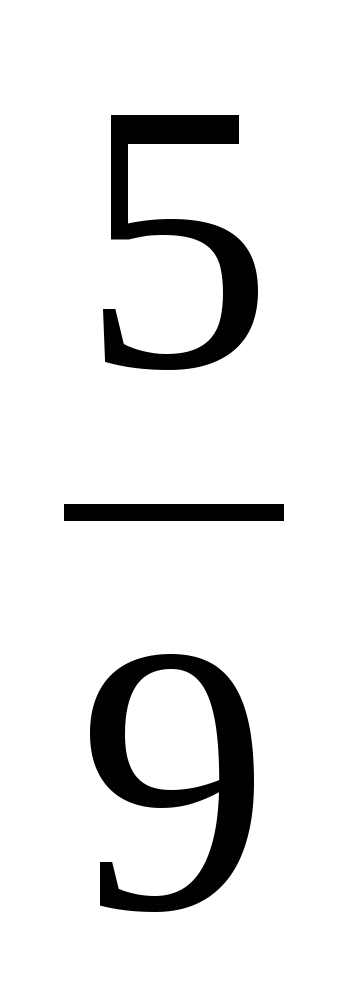 2)
2) 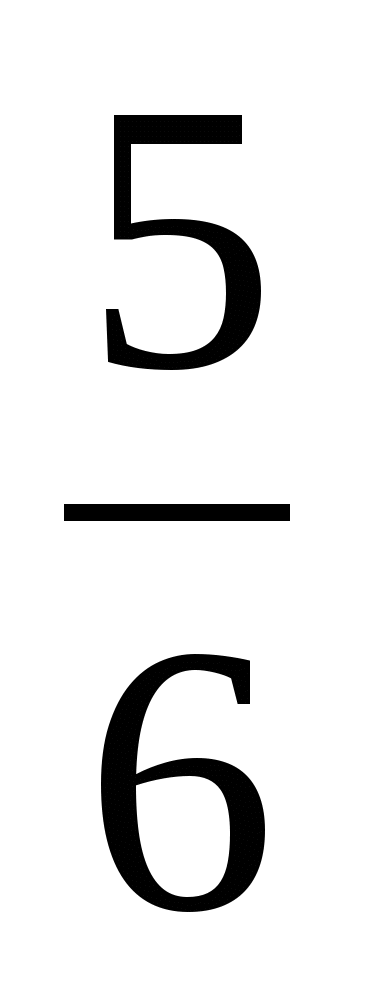 3) 1 4) 2
3) 1 4) 2
2. Вычислите 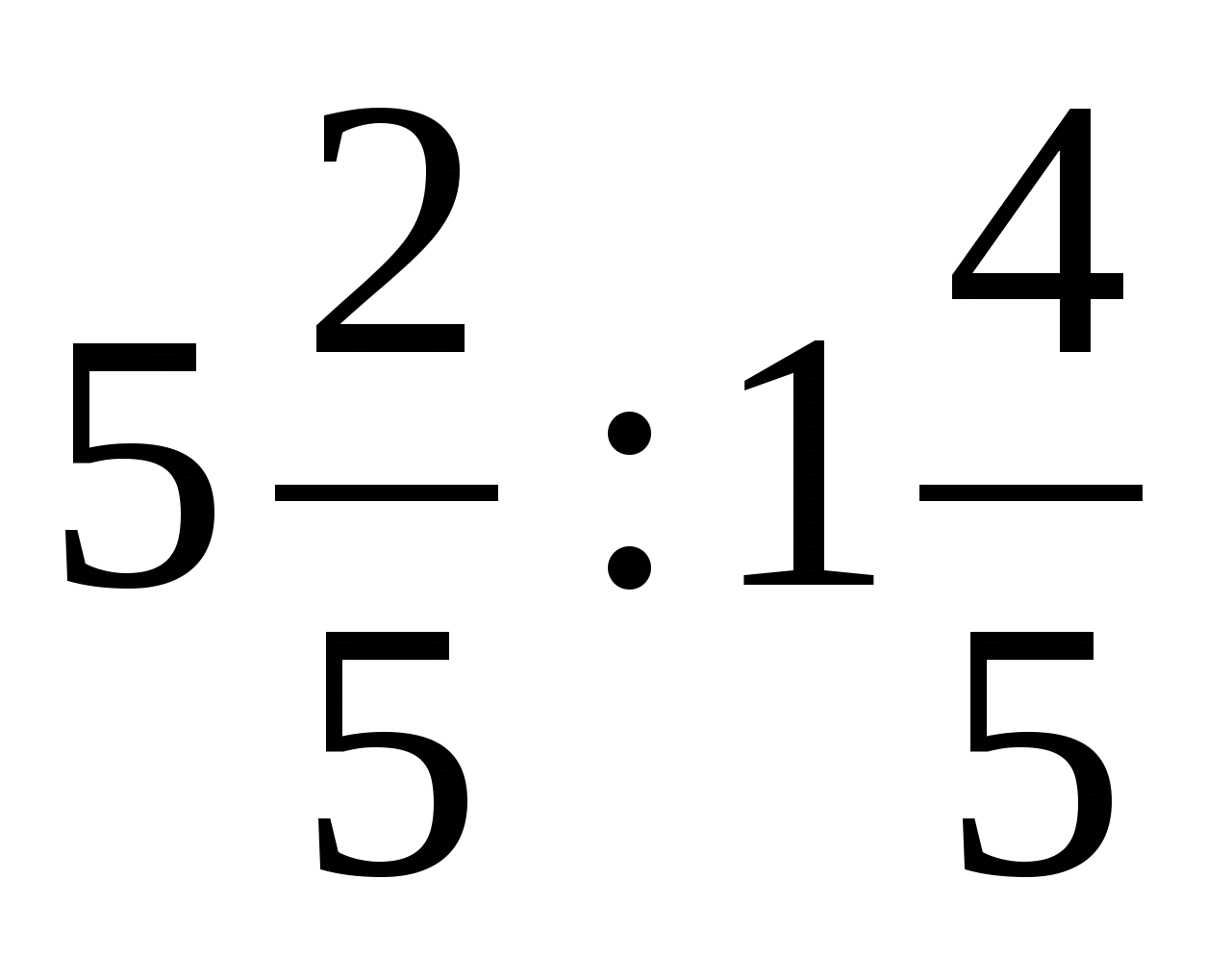
1) 3 2) 4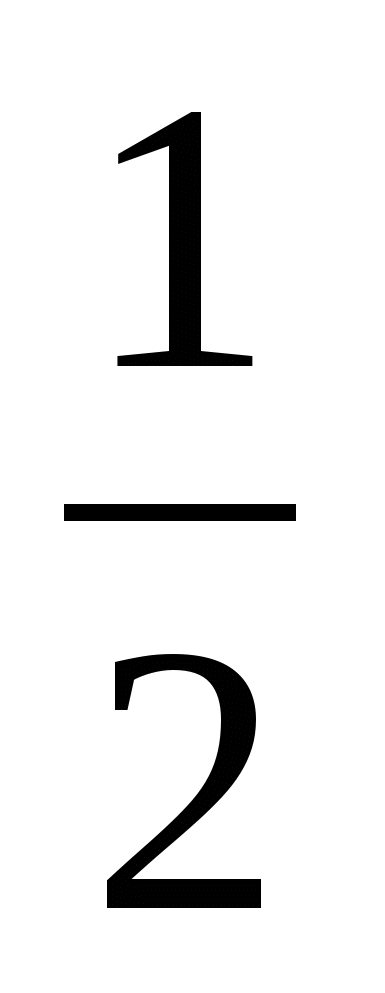 3) 5
3) 5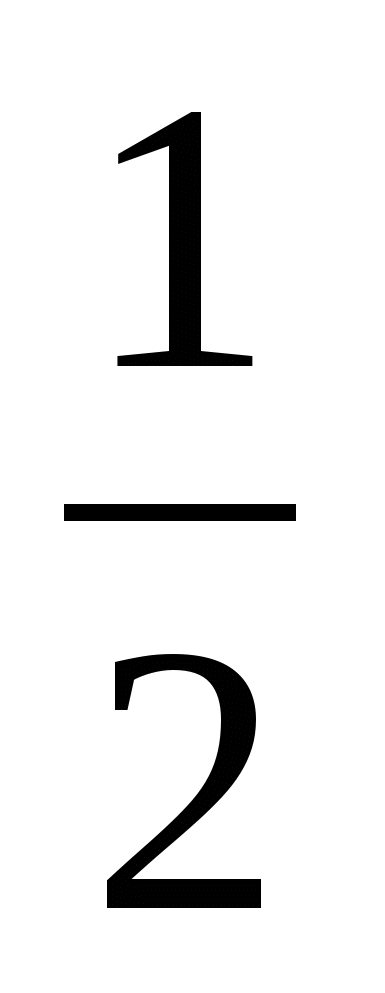 4)
4)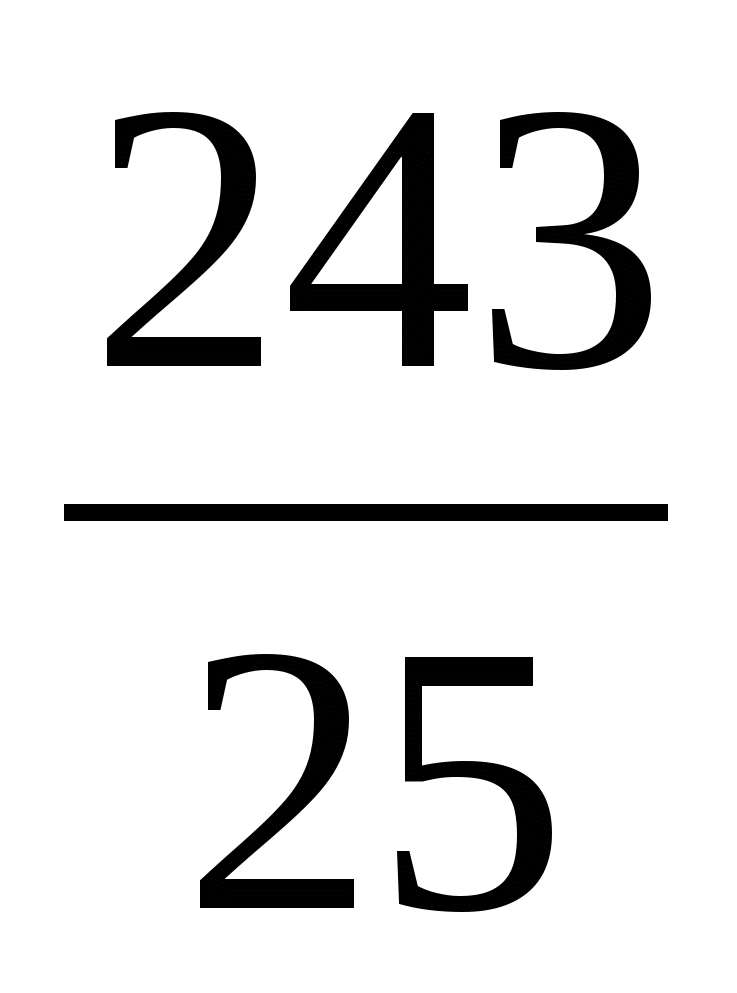
3. Решите уравнение.
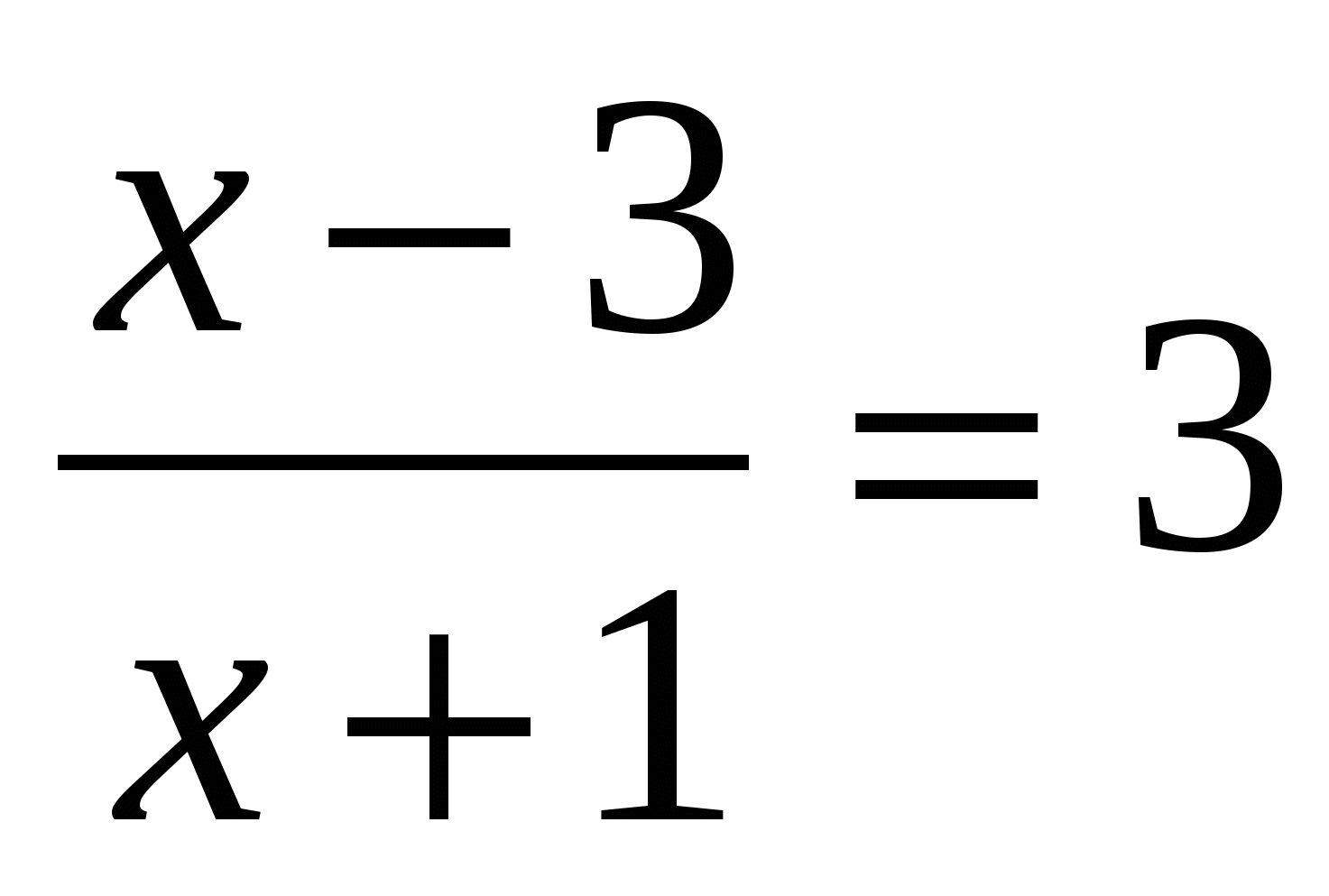
Ответ: _____________
4.Решите уравнение.
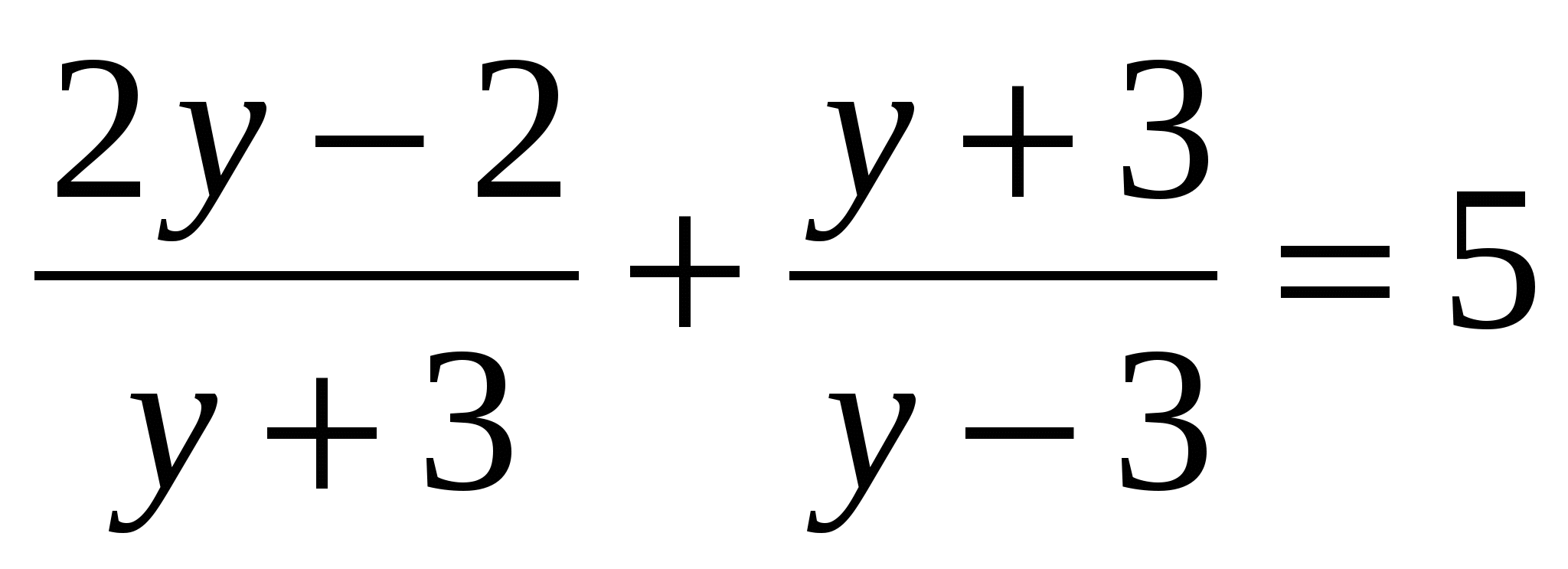
1) 5; -5 2) -6 ; 5 3) -5; 6 4) 4; 6
5. Решите уравнение.
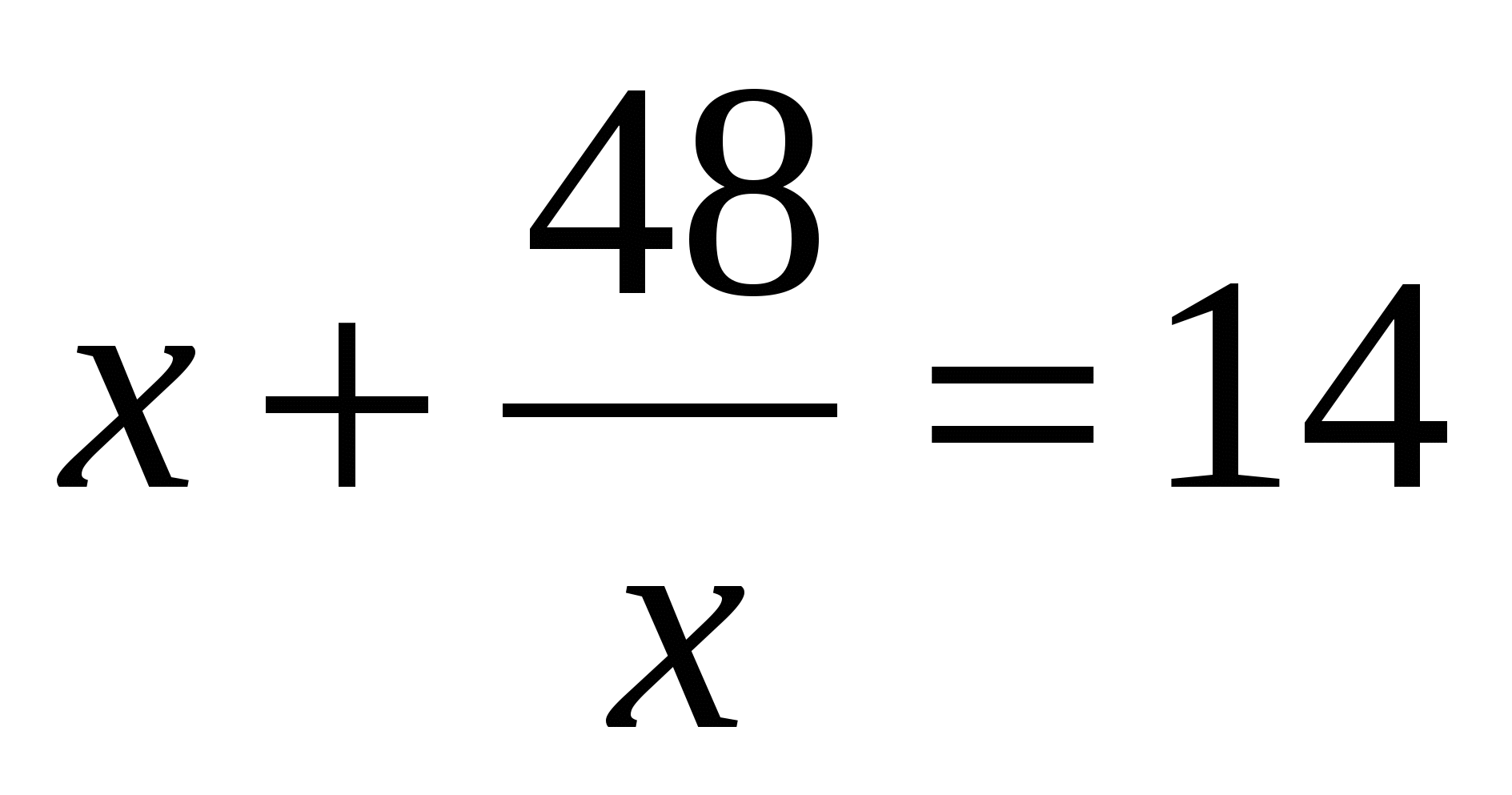
Ответ: _____________
Голубая карточка.
1. Найдите значение выражения.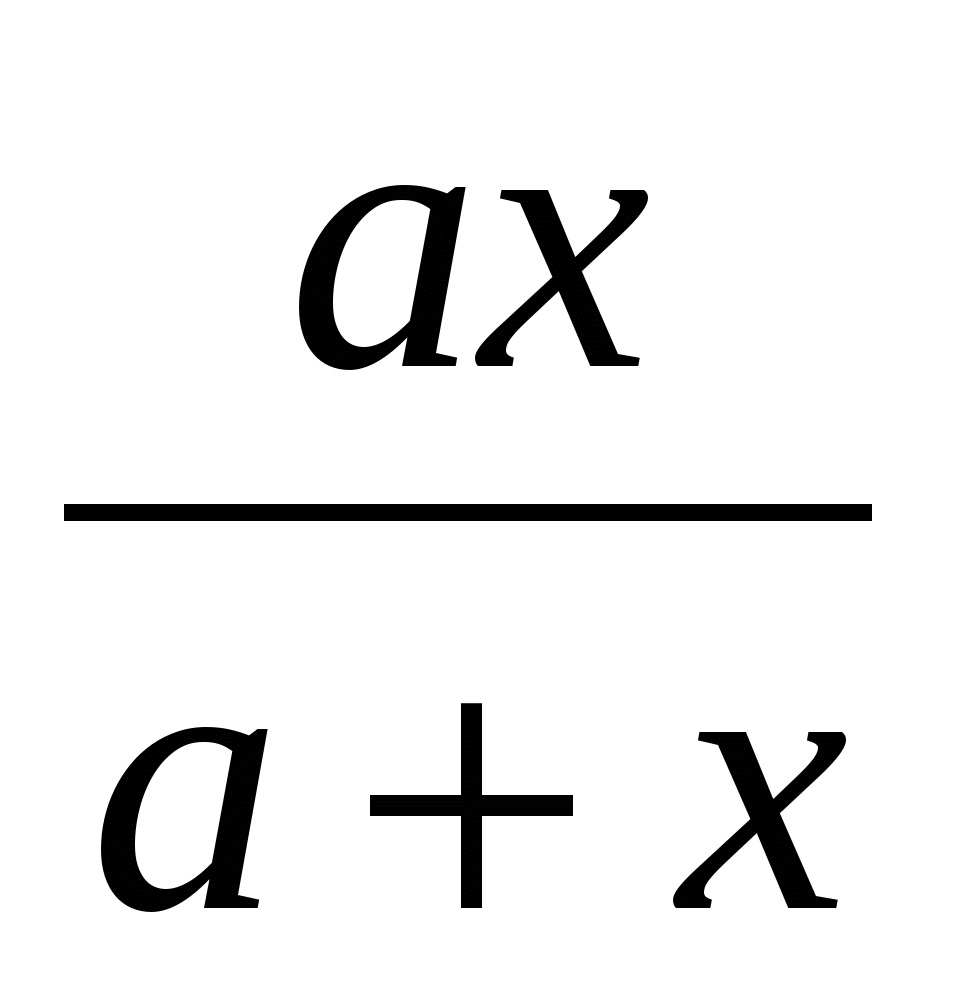 при
при 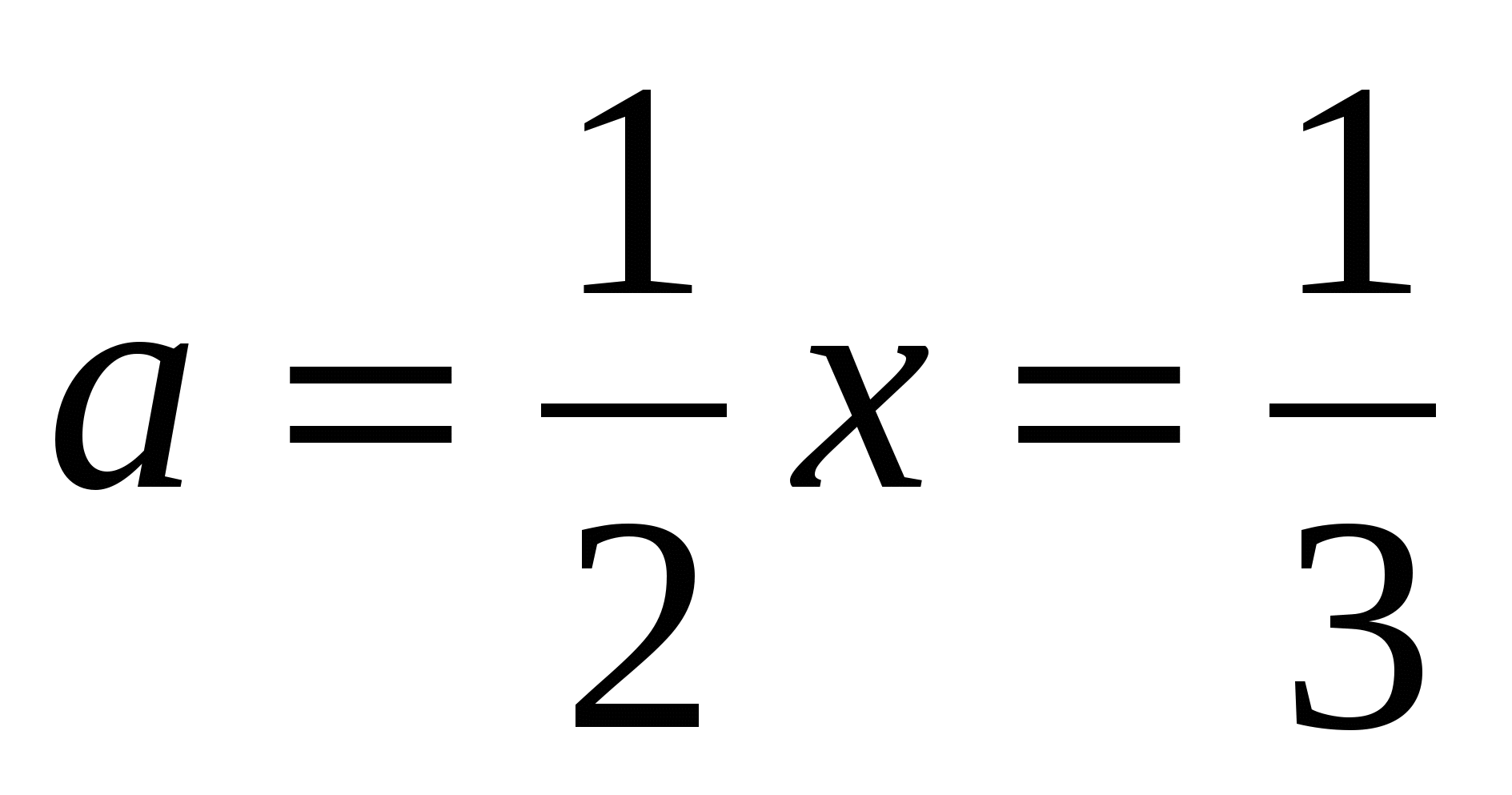
1)0,2 2) -1,5 3) – 0,2 4) 5
2.Найдите значение выражения.
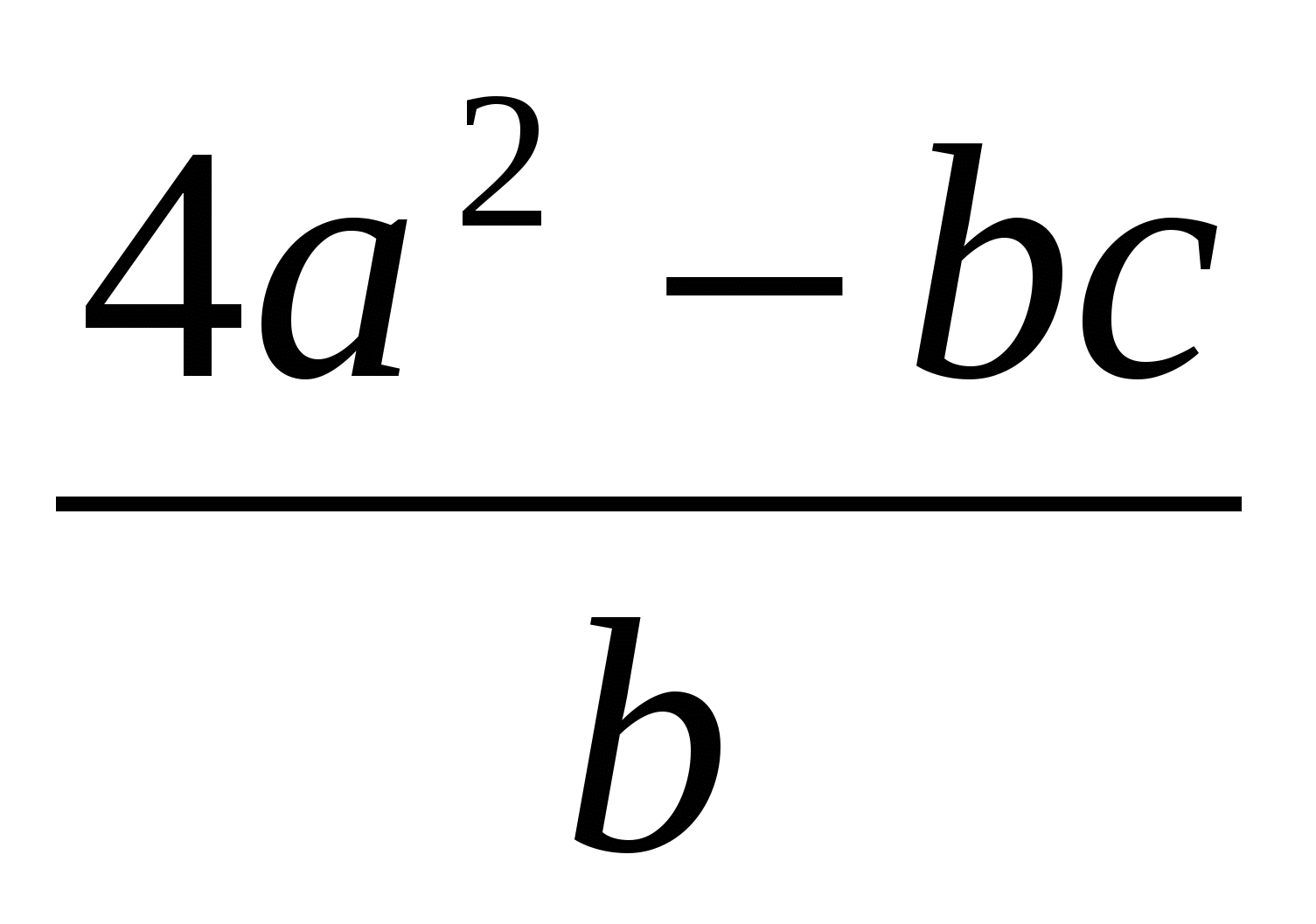 при
при 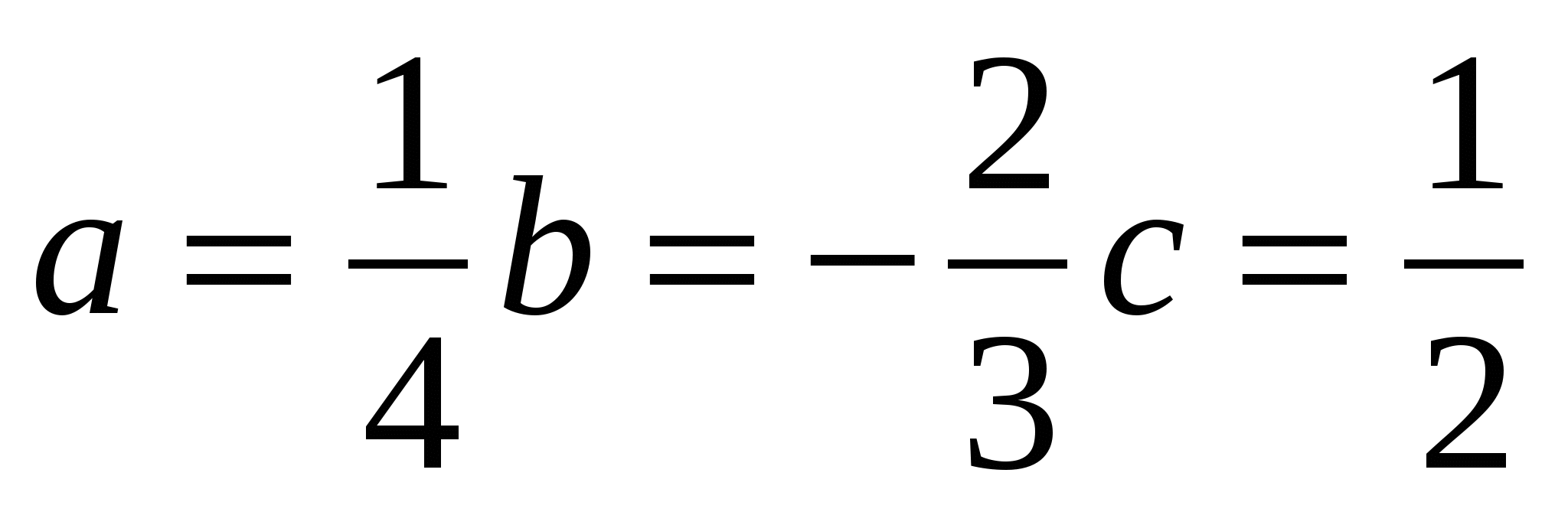
1) -1,5 2)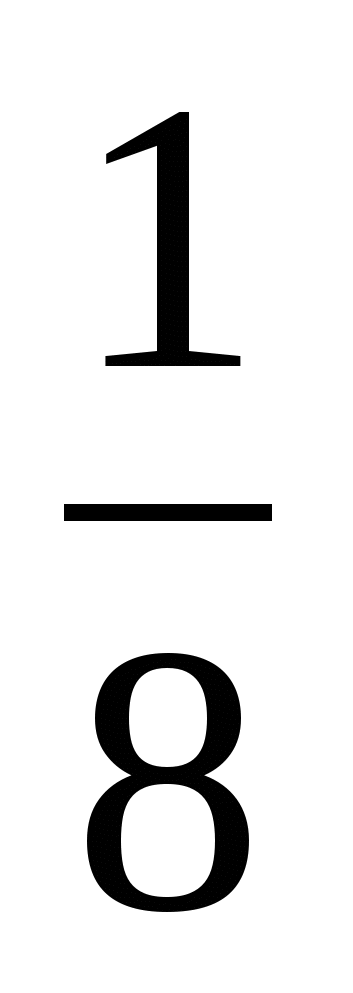 3) -
3) -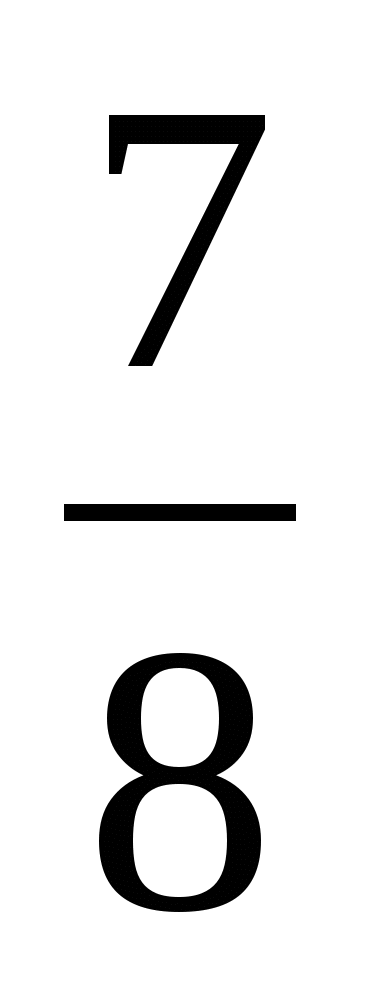 4) -
4) - 
3. Решите уравнение.
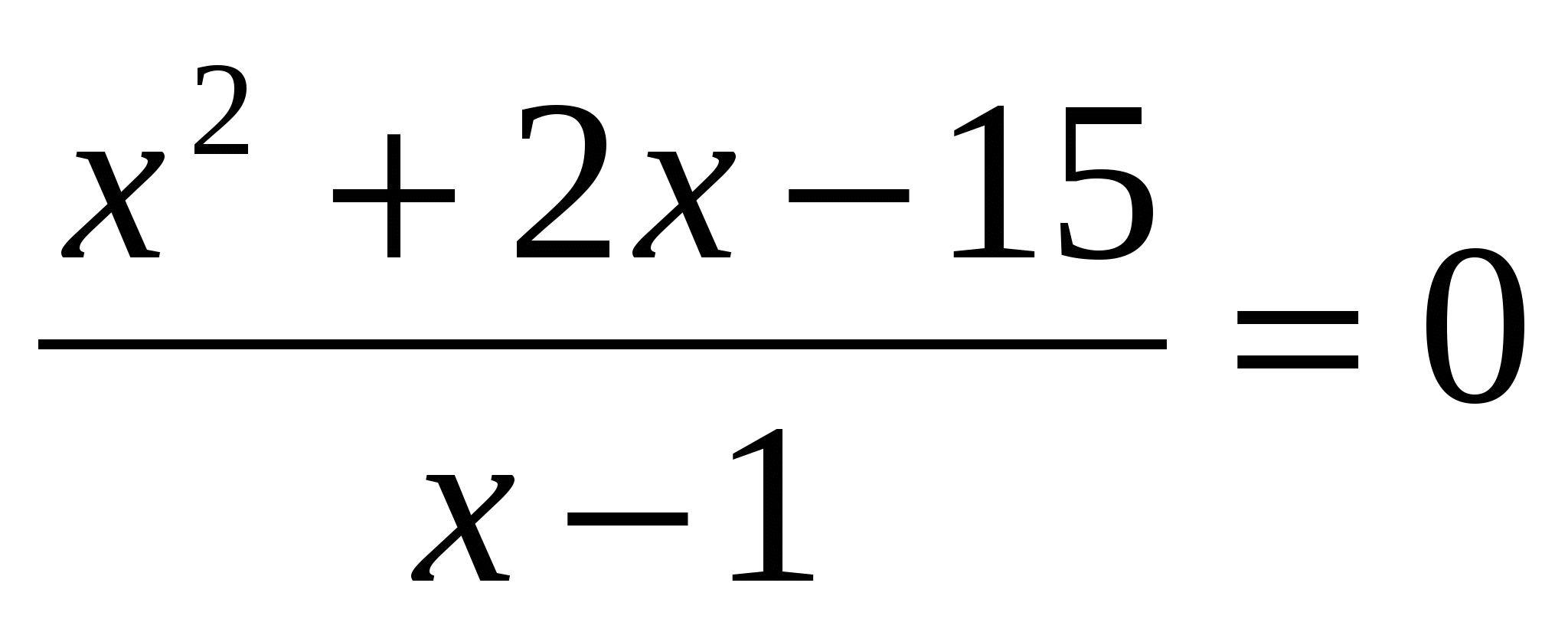
Ответ: ______________
4.Решите уравнение. 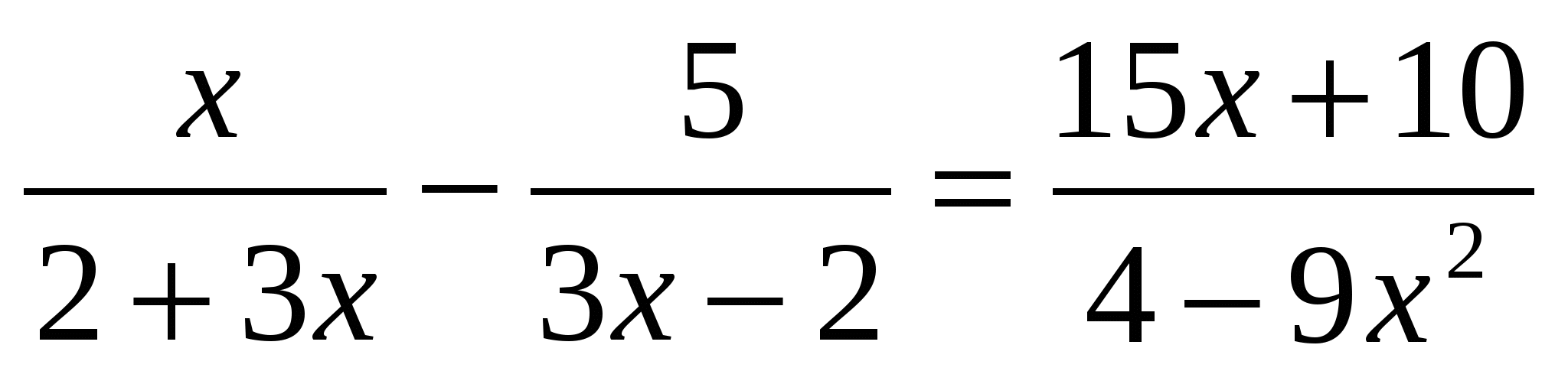
Ответ:___________
Решите уравнение.
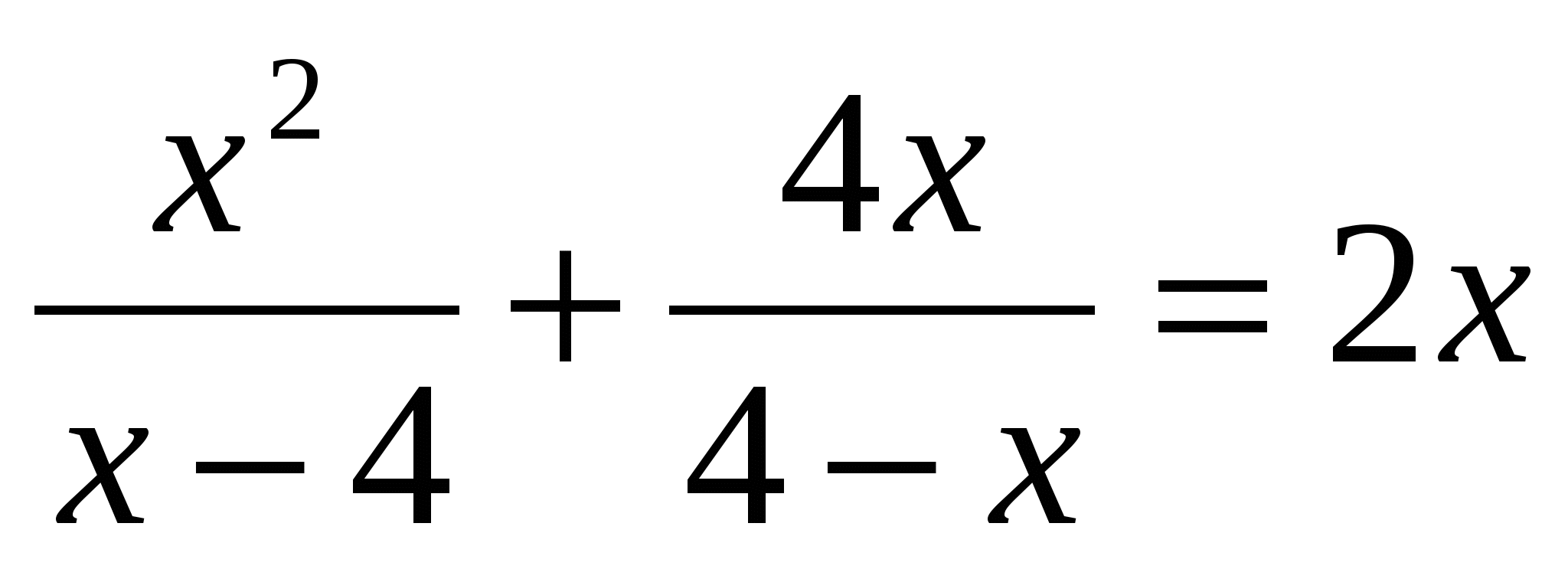
1) 0 2) 4; 0 3) -4 ; 0 4) 4,5; 0,2
Розовая карточка.
Найдите значение выражения.
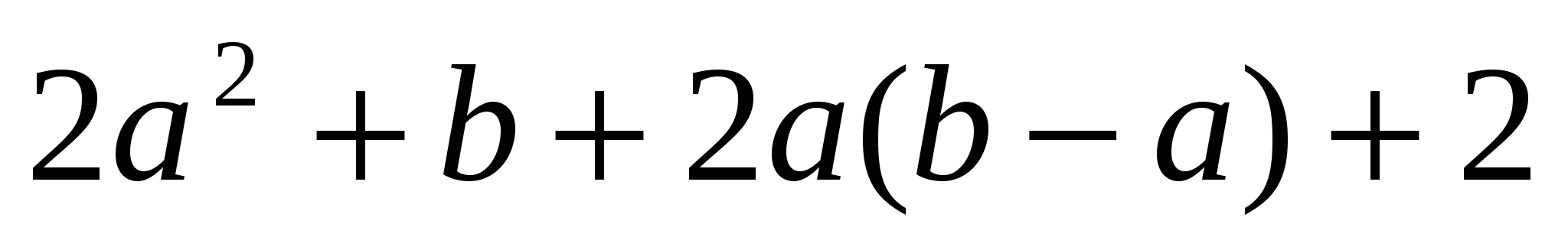 при а=0,5 b=-1
при а=0,5 b=-1 
1) 0 2) -1 3) -2 4)1
2. Найдите значение выражения.
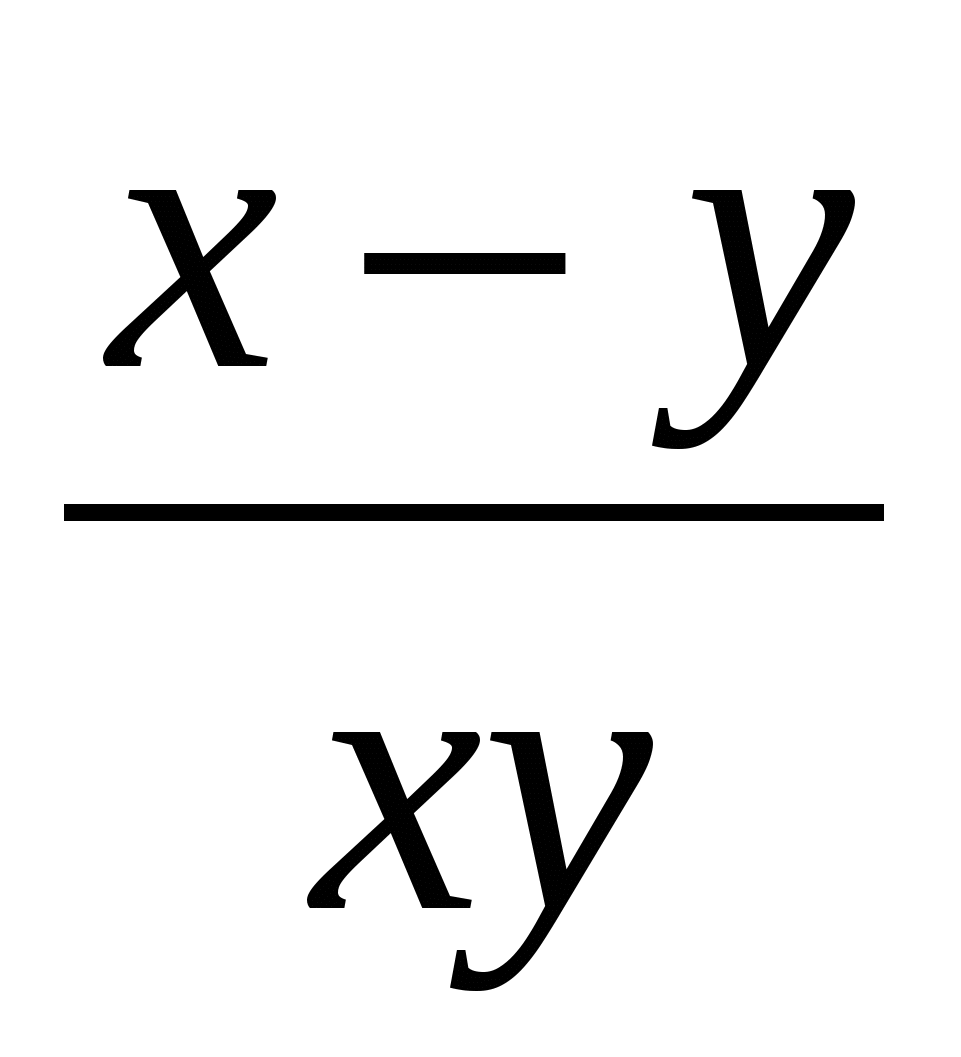 , если y=
, если y=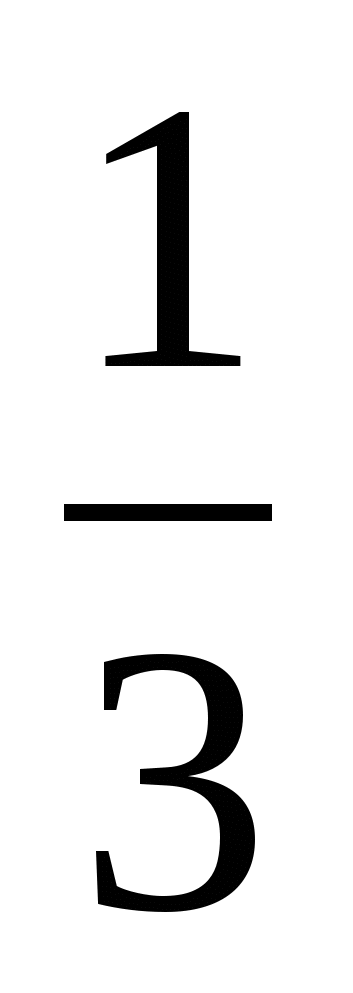 x=
x=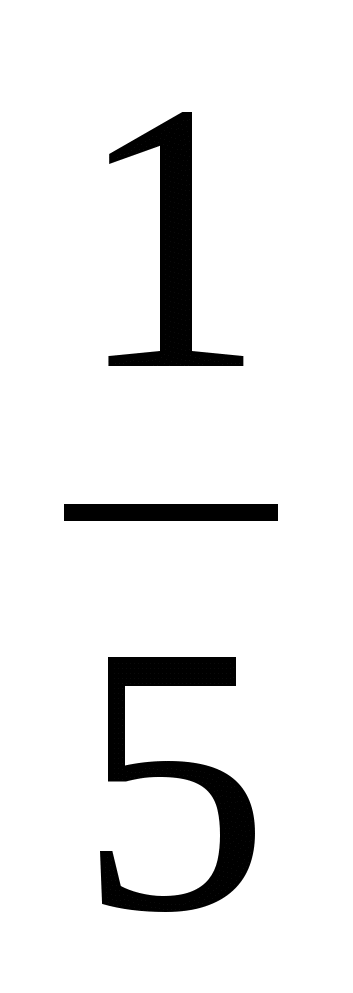
1) -2 2) 7,5 3) 2 4) -7,5
3) Решите уравнение.
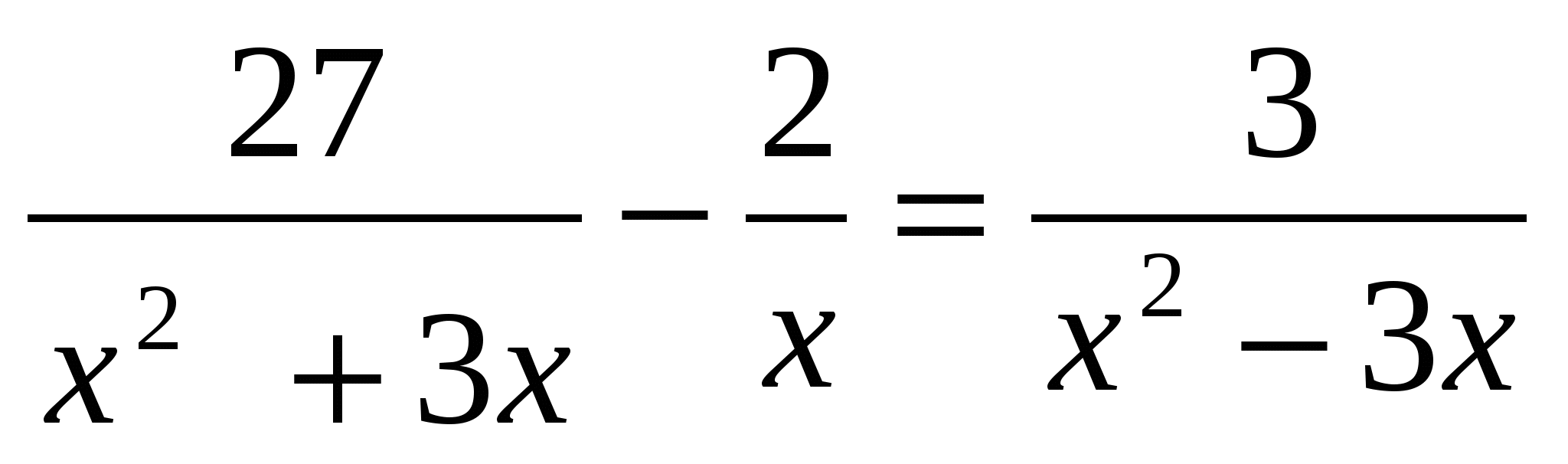
Ответ:_____________
4) Решите уравнение.
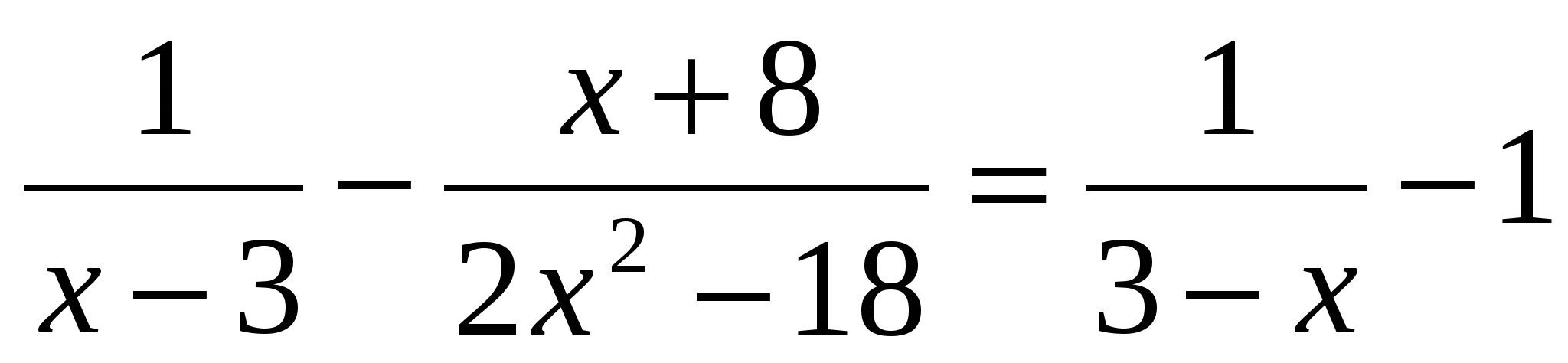
Ответ:______________
5)Решите уравнение.
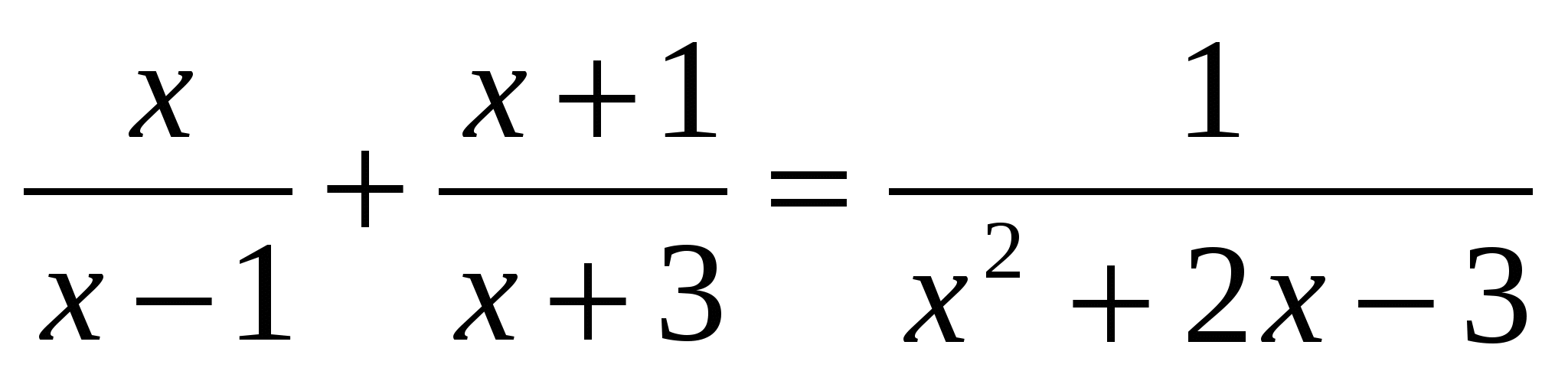
1) 1,2: 5 2) -2 ; 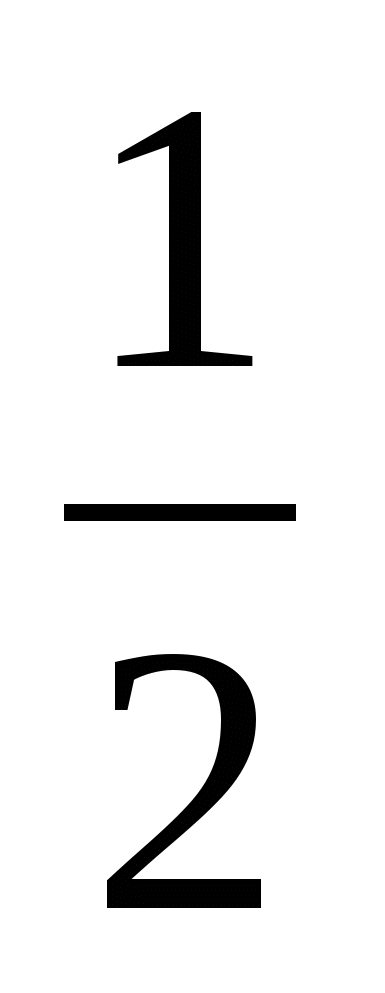 3) 2; -
3) 2; -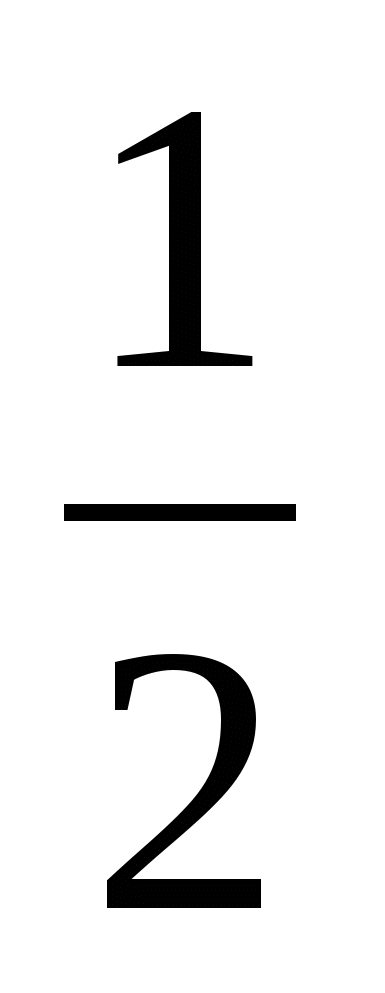 4) 4; -1,5
4) 4; -1,5
6 этап урока- Подведение итогов. Комментарии по домашнему заданию (2минуты).
Учитель обращает внимание учащихся на те теоретические факты и типы уравнений, которые вспоминали на уроке, говорит о необходимости выучить алгоритм решения уравнений. Отмечает наиболее успешную работу на уроке отдельных учащихся , при необходимости выставляет оценки. В качестве домашнего задания учащиеся обмениваются вариантами самостоятельной работы и получают по варианту из предыдущей контрольной работы.
Список использованной литературы:
1. Макарычев Ю.Н. Алгебра.8 класс.- М.:«Просвещение»,2010
2.Макарычев Ю.Н. Уроки алгебры в 8 классе.- М.:«Просвещение»,2010
3.Жохов В.И. Дидактические материалы для 8 класса.-М.:«Просвещение»,2010
Семенко Е.А. Технология разноуровневого обобщающего повторения по математике .- «Просвещение -Юг»,2008 год