Урок в 9 классе «Уравнения с одной переменной» | Лучшие рефераты, дипломные, курсовые работы

Комитет по народному образованию Администрации Солнечногорского муниципального района

МУНИЦИПАЛЬНОЕ КАЗЁННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ПОВАРОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА

141540 Московская область, Солнечногорский район, посёлок Поварово

672-375 – канцелярия; учительская; povar.school@mail.ru

672-385 – директор; факс.

Урок в 9 классе

«Уравнения с одной переменной»

Разработала Морозова Н.С., учитель математики высшей квалификационной категории МКОУ Поваровской СОШ

2012

Тема урока «Уравнения с одной переменной».

Цель урока – рассмотреть решения целых уравнений различных типов путём введения новой переменной.

Задачи урока:

- закрепить знания учащихся по решению уравнений, способствовать выработке навыков решения уравнений;

- применение знаний, умений, навыков при решении различных типов уравнений;

- развитие навыка самостоятельности в работе.

Оборудование: интерактивная доска, слайды.

Ход урока.

Мобилизующее начало урока: сообщение темы, цели и хода урока.

Проверка выполнения домашнего задания:

а) групповая перед уроком самими учащимися;

б) слайд № 1: учитель отвечает на возникшие вопросы при выполнении

домашней работы по своему решению;

в) выборочная ( во время устной работы класса 4 «слабых» ученика выполняют самостоятельно по своему усмотрению одно из заданий из домашней работы на листочках ) – учитель отвечает на вопросы и оценивает работу каждого.

3. Устная работа ( в это время на доске 3 ученика выполняют самостоятельно работу по карточкам ) – учитель проверяет, отвечает на вопросы и оценивает работу каждого.

Карточка № 1:

Решить уравнение: 3х² + 3 _ 2 – 4х - 2 [ Ответ: -2; 1⅓].

5 10 -

Карточка № 2:

Решить уравнение: 3х⁴ – 2х² – 1 = 0 [ Ответ: 1; -1].

Карточка № 3:

Решить уравнение : ( х² – 4 ) ( х²+ 4 ) – (26х²- 41)=0 [Ответ:1; -1; 5; -5]

Слайды № 2, 3, 4.

4. Решение целых уравнений различных типов.

Задание № 1.

Решить уравнение ( х²– 7 )² – 4( х² – 7) – 45 = 0.

Проблемная ситуация.

Вопросы учителя: C каким видом уравнения можно сравнить данное? Как к нему прийти? Знаем ли этот способ?

Оформление решения показывает учитель.

Введём новую переменную у = х²-7.

Тогда уравнение примет вид :

у² – 4у – 45 = 0;

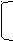у = 9,

у = -5.

Имеем, х² – 7 = 9 или х² – 7 = -5

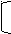
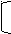х = 4, х = √2,

х = -4. х = -√2.

Ответ: 4; -4; √2; -√2.

Задание № 2.

Решить уравнение:

а) (х² – х + 1) (х² – х – 7 ) = 65 Обсуждается способ решения. Способ найден. Ученики пытаются выполнить задание самостоятельно, при необходимости учитель консультирует индивидуально. По желанию 3 ученика решают на доске. Учитель отвечает на вопросы, проверяет и оценивает работу.

Ответ: а) 4; -3 б) 1; -1; 5; -5.

Задание № 3. Самостоятельная работа слабых учеников в паре на листочках. Учитель собирает, проверяет и оценивает работы.

УМК Ю.Н.Макарычев и др. №276 (а,в).

Ответы ученики проверяют по учебнику. Можно пользоваться шаблоном решения из рабочей тетради.

Задания № 4, 5, 6. Работа с сильными учениками.

Слайд № 5 – ученикам предлагаются 3 уравнения :

- рассматривается первое уравнение;

- способ решения найден;

- желающие продолжают решение на доске;

- группа учеников ищут решение второго уравнения;

- после проверки решения первого уравнения обсуждается способ решения второго и т.д.;

- учитель поощряет учеников оценками за предложенные идеи.

Учитель консультирует, отвечает на вопросы, проверяет и оценивает работу.

Задание № 4.

Решить уравнение: (х + 1)(х + 3)(х + 5)(х + 7) = 945.

Проблемная ситуация - уравнение другого вида, но почему то рассматривается сейчас, когда применяем метод введения новой переменной.

Учитель рассматривает все предложения учеников. Способ решения – заменить трёхчленами произведение крайних множителей и произведение средних множителей.

Решение: ( х² + 8х + 7 ) ( х² + 8х + 15) = 945.

Введём новую переменную у = х²+ 8х.

Тогда уравнение примет вид:

( у + 7) ( у + 15) = 945;

у² + 22 у – 840 = 0;

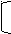у= -42;

у= 20.

Имеем, х² + 8х = -42 или х² + 8х = 20.

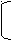нет корней х = -10;

х = 2.

Ответ: -10; 2.

Задание № 5.

Решить уравнение:

(х² +2х)² – (х + 1)² = 55;

Проблемная ситуация: данное уравнение в этой теме, почему? Значит, можно решить путём введения новой переменной. Как преобразовать левую часть уравнения? Способ решения найден – ( х + 1)² = х² + 2х + 1.

Ответ: -4; 2.

Задание № 6.

Решить уравнение : х² – 4 + х - 3⅓

х х² -4-

Проблемная ситуация: данное уравнение в этой теме, почему?

Способ решения найден. Вводим новую переменную У = х² – 4

Уравнение примет вид: у + 1 = 3⅓

Ответ: 4; -1; 1 + √145; 1 - √145

6 6

5. Домашнее задание :

Обязательный уровень: УМК Ю.Н. Макарычев и др. № 276(б,г), №282(а);

Творческий уровень: №274 (а), №370(а).