Урок–игра « Удивительный мир чисел»
Цели:
Развивать математические и творческие способности на основе заданий, носящих нестандартный занимательный характер
Формировать навыки исследовательской работы
Формировать представление о математике как о части общечеловеческой культуры
Воспитывать культуру межличностного и группового общения
Оборудование: таблица простых чисел, компьютер, презентация
Ход игры:
1. Организационный момент. Вступительное слово учителя.
Учитель: Здравствуйте, ребята. Урок наш будет необычным. Сегодня мы с вами совершим путешествие в удивительный мир чисел./Слайд №1 /. Предлагаю разбиться на команды, придумать название команде и отправится в путь.
2. Игра: Скажите, какие числа вы знаете? /четные и нечетные, простые и составные, целые и дробные, положительные и отрицательные…/. А еще есть числа треугольные, квадратные, пятиугольные /Слайд №2/. А слышали ли вы о числах мужественных и женственных? В Древнем китайском манускрипте ( более 4000 лет до н.э.) четные числа назывались женственные, а нечетные- мужественными. /Слайд №3/.
Задание 1: /Слайд № 4/ (ответ: 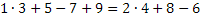 или
или 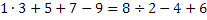 )
)
Команда, которая первая выполнила задание, получает 3 балла. Команда, которая выполнила задание позже , но может предложить другой вариант решения, получает 2 балла.
Учитель: А сейчас мы с вами познакомимся с дружественными числами /Слайд №5/. Два натуральных числа называются дружественными, если сумма натуральных делителей одного из них равна другому числу и наоборот( сами числа в состав делителей не входят). История дружественных чисел теряется в глубине веков. По свидетельству античного философа Ямвлиха ( 3-4 век) великий Пифагор на вопрос ,кого следует считать своим другом, ответил: « Того, кто является моим вторым Я, как числа 220 и…» /Слайд №6/
Задание2: Какое число имел ввиду Пифагор? ( при выполнении этого задания снова демонстрируется слайд №5). (ответ: 284)
Команда, нашедшая второе число получает 2 балла. Команда, успевшая выполнить еще и проверку того, что число 284 является дружественным для 220, получает 3 балла.
Демонстрируется слайд №7. Комментарии к слайду №7: « Долго считалось, что следующую пару дружественных чисел 17296 и 18416 открыл в 1636 году знаменитый французский математик Пьер Ферма. Но недавно в одном из трактатов арабского ученого Ибн аль- Банны (1256-1321) были найдены строки: «Числа 17296 и 18416 являются дружественными. Аллах всеведущ». В 1747-1750 годах Леонард Эйлер провел уникальные числовые «раскопки»: он придумал оригинальные методы поиска и обнаружил сразу 61 новую пару дружественных чисел. Примечательно, что среди них оказались и нечетные числа 69 515 и 1 1498 455. Сейчас известно 1100 пар дружественных чисел. Любопытно, что в 1866 году итальянский школьник Никколо Паганини( однофамилец великого скрипача) нашел пару дружественных чисел 1184 и 1210, которую все, в том числе и выдающиеся математики, проглядели.»
А теперь давайте познакомимся с совершенными числами./ Слад№8/ Совершенное число-число, равное сумме всех своих делителей ( без самого числа).В 4 веке до н. э. Пифагор и его ученики знали только 3 числа. Число 8 128 стало известно лишь в 1 веке н.э., а число 33 550 336- в 15 веке. До сих пор неизвестно, есть ли нечетное совершенное число и существует ли самое большое совершенное число.
Задание №3: /Слайд»8/ Найти два первых совершенных числа( подсказка: 1-ое число однозначное, 2-ое-от 20 до 30)
Команда, нашедшая число 6 получает 1 очко, нашедшая число 28 -2 очка.
Итак, первое совершенное число -6. может быть, поэтому именно шестое место считалось самым почетным на пирах у древних римлян . Второе по старшинству совершенное число -28. В некоторых ученых обществах и академиях полагалось иметь 28 членов. Почти до наших дней дожила эта традиция, идущая из далеких эпох. В Риме в 1917 году при выполнении подземных работ обнаружилось помещении одной из древнейших академий: зал и вокруг него 28 кабинетов- как раз по числу членов академии.
А слышали ли вы про числа- близнецы?/ Слайд №9/. Два простых числа, разность которых равна двум, называются близнецами.
Задание №4: Найдите в таблице простых чисел пары чисел-близнецов.
Команда, нашедшая больше всех пар, получает 2 балла.
3. Подведение итогов.
Учитель: Вот и закончилось наше путешествие. Все хорошо потрудились. Но победила команда… А в заключении мне бы хотелось про читать вам слова немецкого писателя Гессе « Всякая хорошо решенная математическая задача доставляет умственное наслаждение» /Слайд №10/. Помните об этом и решайте больше задач. До свидания.