 Муниципальное бюджетное общеобразовательное учреждение
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №3
Станица Старощербиновская Щербиновского района Краснодарского края
Задачи на совместную работу
ЕГЭ Задание В13
подготовила
учитель математики
Тихончук Людмила Юрьевна
Ст.Старощербиновская
2013
Как решить задачу на совместную работу ?
Задачи на совместную работу знакомы школьникам многих поколений. Они нередко предлагаются на итоговой аттестации, однако времени на их решение в школьном курсе математики отводится очень немного.
Задачи на работу делятся на два типа:
задачи, в которых выполняется раздельная работа – эти задачи решаются аналогично задачам на движение
задачи на совместную работу.
Если в задаче встречаются слова «выполнили работу вместе» или слова «совместная работа», значит это задача на совместную работу.
В этой статье я подробно остановлюсь на алгоритме решения задач на совместную работу.
1. В задачах на совместную работу мы имеем дело с теми же тремя параметрами, что и в задачах на раздельную работу:
А-объем работы,
t-время,
V-производительность
которые связаны между собой формулами:
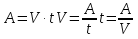
Разбор задач :
1.Производительности отца и сына относятся как 8:4. Сначала в течение трех часов они обрабатывали земельный участок вместе, затем отец устал и пошел отдыхать. Сколько необходимо времени сыну, чтобы завершить самостоятельно обработку участка, если известно, что при совместной работе сын и отец на обработку участка
потратили бы ровно 5 часов? Ответ запишите в часах.
Производительности отца и сына относятся как 8:4.
Производительность(V)
Время (t)
Работа(A)
О
8х
С
4х
О+С
О+С
Сначала в течение трех часов они обрабатывали земельный участок вместе
Производительность(V)
Время (t)
Работа(A)
О
8х
С
4х
О+С
12х
3
36х
О+С
Сколько необходимо времени сыну, чтобы завершить самостоятельно обработку участка, если известно, что при совместной работе сын и отец на обработку участка потратили бы ровно 5 часов?
Производительность(V)
Время (t)
Работа(A)
О
8х
С
4х
О+С
12х
3
36х
О+С
12х
5
60х
Производительность(V)
Время (t)
Работа(A)
О
8х
С
4х
60х-36х
О+С
12х
3
36х
О+С
12х
5
60х
Производительность(V)
Время (t)
Работа(A)
О
8х
С
4х
24х:4х=6
60х-36х
О+С
12х
3
36х
О+С
12х
5
60х
Ответ:6
2. Производительности первого и второго автопогрузчика относятся как 2:8. Сначала второй автопогрузчик проработал ровно 1 час 30 минут самостоятельно. Сколько времени потребуется первому автопогрузчику, чтобы завершить работу самому, если известно, что при совместном выполнении этой же работы им понадобилось бы ровно 4 часа. Ответ дайте в часах.
Производительность(V)
Время (t)
Работа(A)
1
2х
28х:2х=14
40х-12х
2
8х
1,5
12х
1+2
10х
4
40х
Ответ:14
3. Производительности труда отца и сына относятся как 6:3. Для обработки земельного участка при совместной работе им потребовалось бы 4 часа. Однако они обрабатывали участок вместе только первые три часа. Сколько необходимо времени сыну, чтобы завершить самостоятельно обработку участка? Ответ запишите в часах.
Производительность(V)
Время (t)
Работа(A)
О
6х
С
3х
9х:3х=3
36х-27х
О+С
9х
3
27х
О+С
9х
4
36х
Ответ:3
4. Производительности двух копировальных автоматов относятся как 6:4. Обычно при совместной работе автоматы выполняют заказ за 5 часов. В один из дней, работая над заказом вместе, они проработали ровно 3 часа 30 минут, после чего первый автомат сломался. Сколько времени после этого понадобилось второму автомату,
чтобы закончить заказ одному? Ответ дайте в минутах.
Производительность(V)
Время (t)
Работа(A)
1
6х
2
4х
15х:4х=3,75
50х-35х
1+2
10х
3,5
35х
1+2
10х
5
50х
3,75ч=225 минут Ответ:225
5. Производительности двух копировальных автоматов относятся как 3:2. Известно, что при совместной работе заказ они полностью выполняют за 5 часов. В один из дней над заказом они проработали совместно ровно три с половиной часа, после чего второй автомат сломался и работу над заказом заканчивал первый. Сколько времени
ему на это понадобилось? Ответ дайте в минутах.
Производительность(V)
Время (t)
Работа(A)
1
3х
7,5х:3х=2,5
25х-17,5х
2
2х
1+2
5х
3,5
17,5х
1+2
5х
5
25х
2,5 ч=150минут Ответ: 150
6. Производительности труда мастера и ученика относятся как 7:5. Обычно, если мастер и ученик работают над заказом вместе, то этот заказ они выполняют за 3 часа. Однажды ученик задержался и сначала мастер сам работал над заказом в течение 2-х часов. К этому времени присоединился к выполнению заказа ученик. Сколько времени понадобилось мастеру и ученику, чтобы завершить работу? Ответ дайте в минутах.
Производительность(V)
Время (t)
Работа(A)
М
7х
2
14х
У
5х
М+У
12х
22х:12х=11/6
36х-14х
М+У
12х
3
36х
11/6ч=110минут Ответ:110
7. Производительности труда первого и второго маляра относятся как 6:5. Для выполнения заказа при совместной работе им требуется 3 часа. Первый маляр начал работу самостоятельно, но проработал только 30 минут. Сколько понадобится времени второму маляру, чтобы закончить всю работу самому? Ответ дайте в часах.
Производительность(V)
Время (t)
Работа(A)
1
6х
0,5
3х
2
5х
30х:5х=6
33х-3х
1+2
11х
3
33х
Ответ: 6
8. Производительности первого и второго автопогрузчика относятся как 7:4. Для совместного выполнения некоторой работы им требуется 3 часа. Сначала первый автопогрузчик проработал 4 часа самостоятельно. Сколько времени требуется второму автопогрузчику, чтобы завершить работу самому? Ответ дайте в часах.
Производительность(V)
Время (t)
Работа(A)
1
7х
4
28х
2
4х
5х:4х=1,25
33х-28х
1+2
11х
3
33х
Ответ: 1,25
9. Производительности 1 и 2 автомата относятся как 4:3. Обычно автоматы работают над заказом по следующей схеме: сначала они работают вместе в течение 2 часов, а потом 2-й автомат заканчивает работу самостоятельно в течение 2 часов. Из-за поломки 1-го автомата работу начал 2-й и проработал самостоятельно 4 часа. К этому
времени 1-й автомат починили. Сколько необходимо времени первому автомату, чтобы самостоятельно закончить выполнение заказа? Ответ запишите в часах.
Производительность(V)
Время (t)
Работа(A)
1
4х
8х:4х=2
20х-12х
2
3х
2
6х
1+2
7х
2
14х
1+2
3х
4
12х
Ответ: 2
10. Производительности труда мастера и ученика относятся как 8:3. Если мастер и ученик вместе работают над заказом, то они выполняют заказ за 7 дней. Сначала в течение 4-х дней мастер сам работал над заказом, а заканчивал работу уже один ученик. Сколько дней работал ученик?
Производительность(V)
Время (t)
Работа(A)
М
8х
4
32х
У
3х
45х:3х=15
77х-32х
М+У
11х
7
77х
Ответ:15
Список использованной литературы
ЕГЭ 2012 Математика .Задача В13.Задачи на составление уравнений. Рабочая тетрадь
Под редакцией А.Л.Семенова и И.В.Ященко М: издательство: МЦНМО 2012г